条件:已知输入序列的自相关系数矩阵和MA模型阶数,求解MA模型参数
q阶MA模型可以表示为:
其自相关函数表示为:
上式为非线性,不能直接求解MA的参数。需要将其转化为AR模型
1.转化为模型
MA模型的系统函数可以表示为:
可以转化为AR模型:
其中
模型与MA模型的关系满足
2. 模型的求解
自相关系数已知,从p=1开始迭代计算
模型的参数
,直到
,作为此时从
模型截断阶数p,求解得到此时的AR模型参数
模型求解得到
个AR模型参数以及白噪声方差
由于不可能无穷大,因此这里对AR模型的参数进行了截断到p阶,p的数量由自定义的threshold决定,当
时默认后面的参数影响较小忽略不计,
为AR模型估计值
。需要注意的是
,在选定threshold时需要注意满足此条件
3.MA模型参数的求解
由于AR模型与MA模型之间的关系满足:
MA参数的求解可以看作上述AR(q)模型的求解
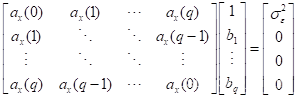
其中的表示由AR(p)模型
参数计算出来的自相关函数
MA模型的求解包含了AR模型的求解。




 本文介绍了如何通过已知输入序列的自相关系数矩阵和MA模型阶数,首先将MA模型转化为AR模型,然后通过迭代计算求解AR模型参数,最后利用AR模型与MA模型的关系确定MA参数。
本文介绍了如何通过已知输入序列的自相关系数矩阵和MA模型阶数,首先将MA模型转化为AR模型,然后通过迭代计算求解AR模型参数,最后利用AR模型与MA模型的关系确定MA参数。
















 3万+
3万+










