8.2.插入排序

一.算法思想：

---

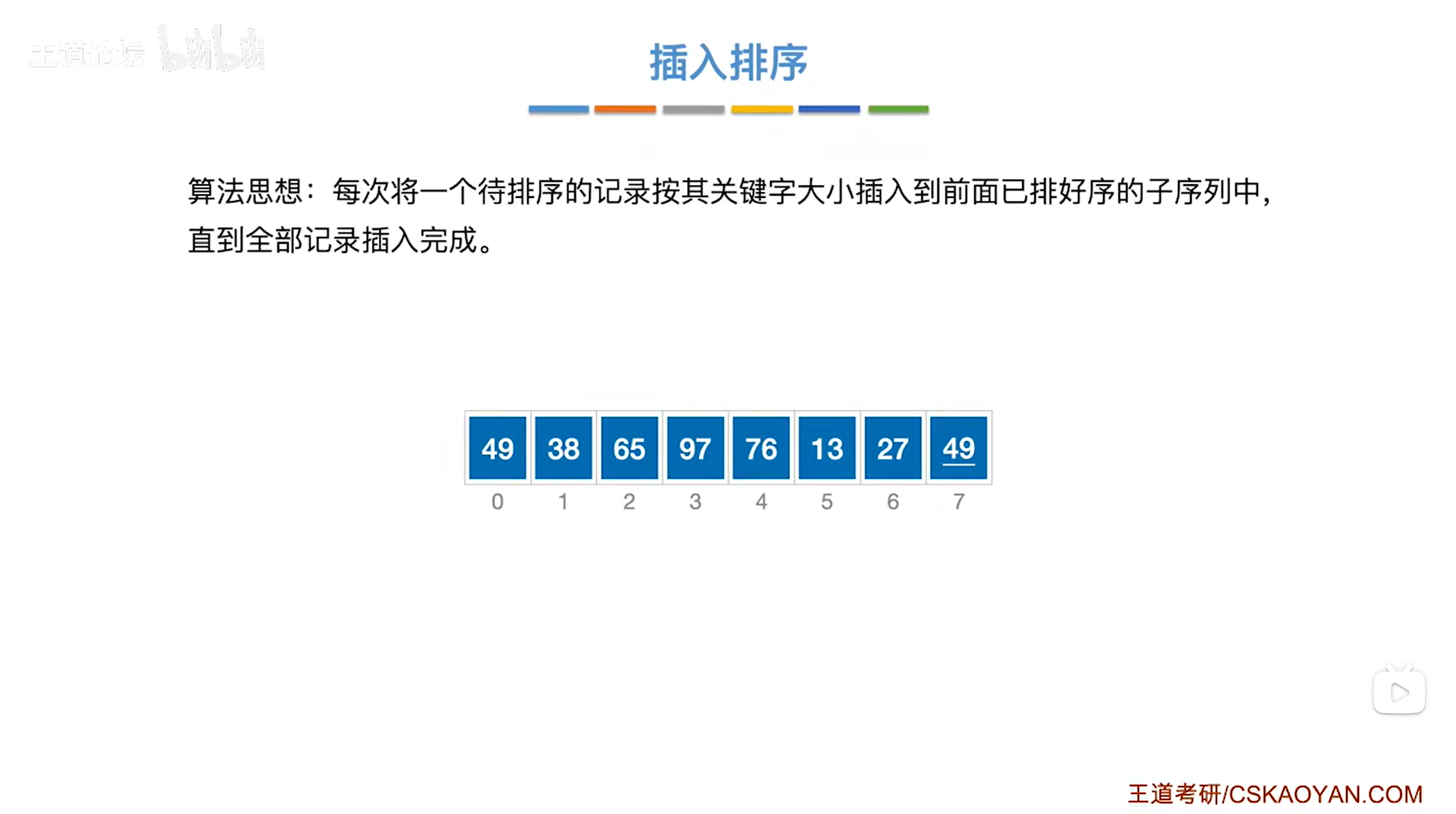
二.实例：

如上图，

要求把上述图片中的数据元素按照递增顺序排序，

初始会从第二个元素即1索引上的38入手，

这是因为插入排序中会认为当前处理的元素之前的部分已经排好序，如果从0索引的元素开始处理，会没有意义，因为一个元素就可以认为有序，所以从1索引的元素开始处理。

38需要与38前面已经排好序的元素依次进行对比，把比38大的元素都依次后移，

38前面已排好序的子序列依次为49，

由于38小于49，所以要把38和49互换位置，

至此，处理完毕，

如下图：

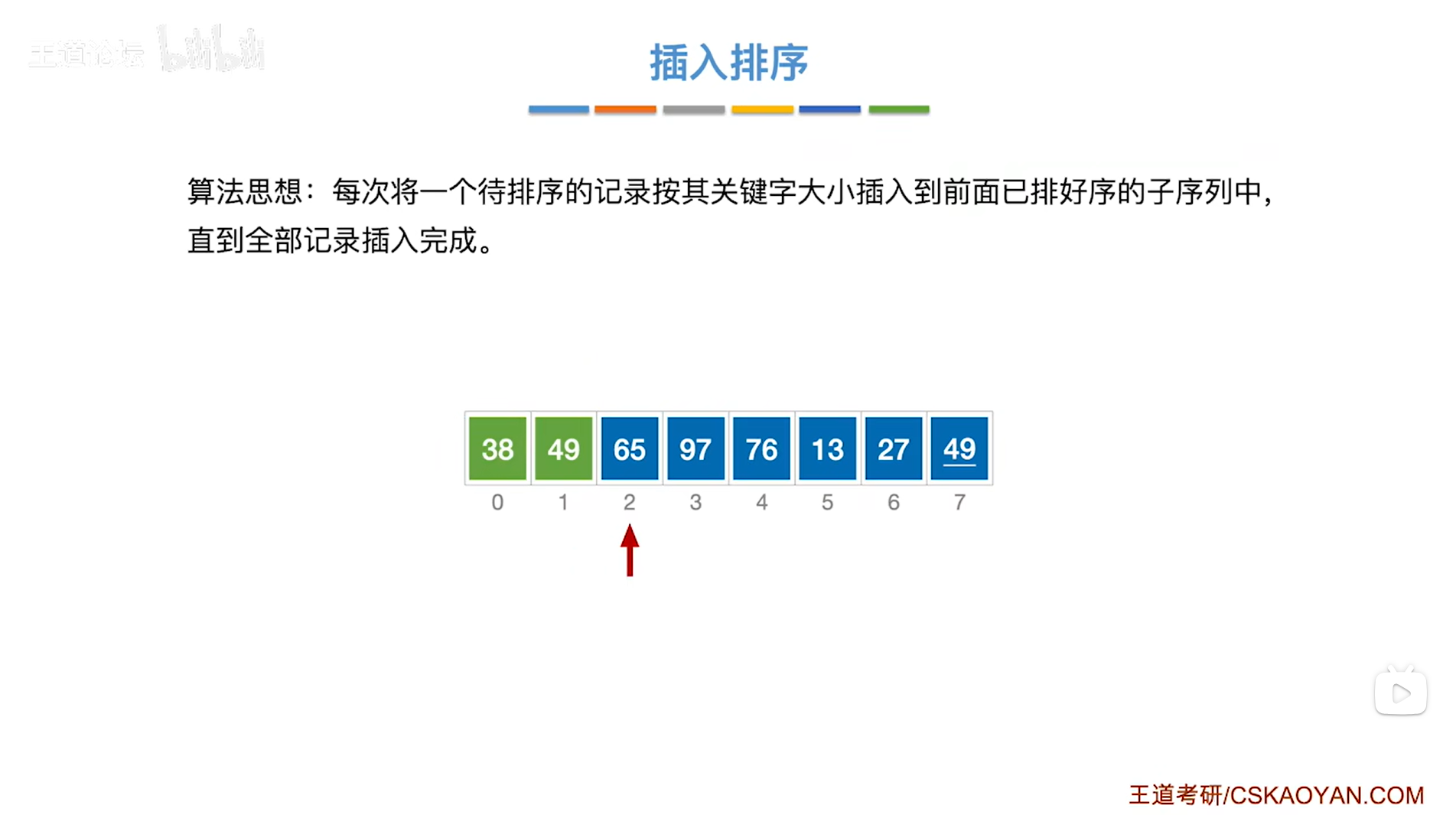
如上图，

接下来要从第三个元素即2索引上的65入手，

65需要与65前面已经排好序的元素依次进行对比，把比65大的元素都依次后移，

65前面已排好序的子序列依次为38、49，

由于65大于49，所以要把65和49无需互换位置（其实这一步就可以确定65是无需移动了，因为65已经比前面的子序列里最大的元素49大了，所以65比整个子序列大，自然就无需移动了，注：子序列是递增排序的），

由于65大于38，所以要把65和38无需互换位置，

至此，处理完毕，

如下图：

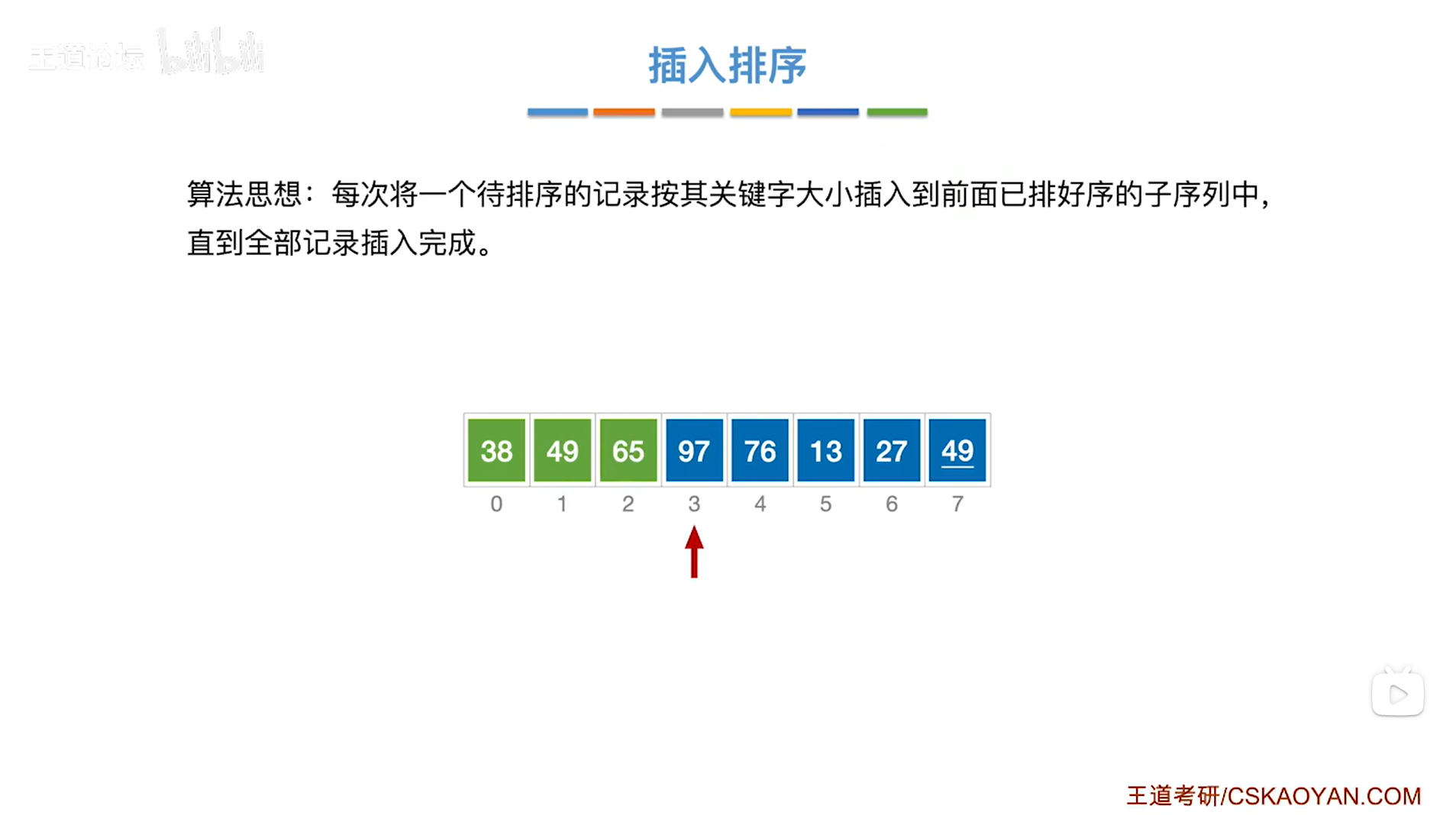
如上图，

接下来要从第四个元素即3索引上的97入手，

97需要与97前面已经排好序的元素依次进行对比，把比97大的元素都依次后移，

97前面已排好序的子序列依次为38、49、65，

由于97大于65，所以要把97和65无需互换位置（其实这一步就可以确定97是无需移动了，因为97已经比前面的子序列里最大的元素65大了，所以97比整个子序列大，自然就无需移动了，注：子序列是递增排序的），

至此，处理完毕，

如下图：

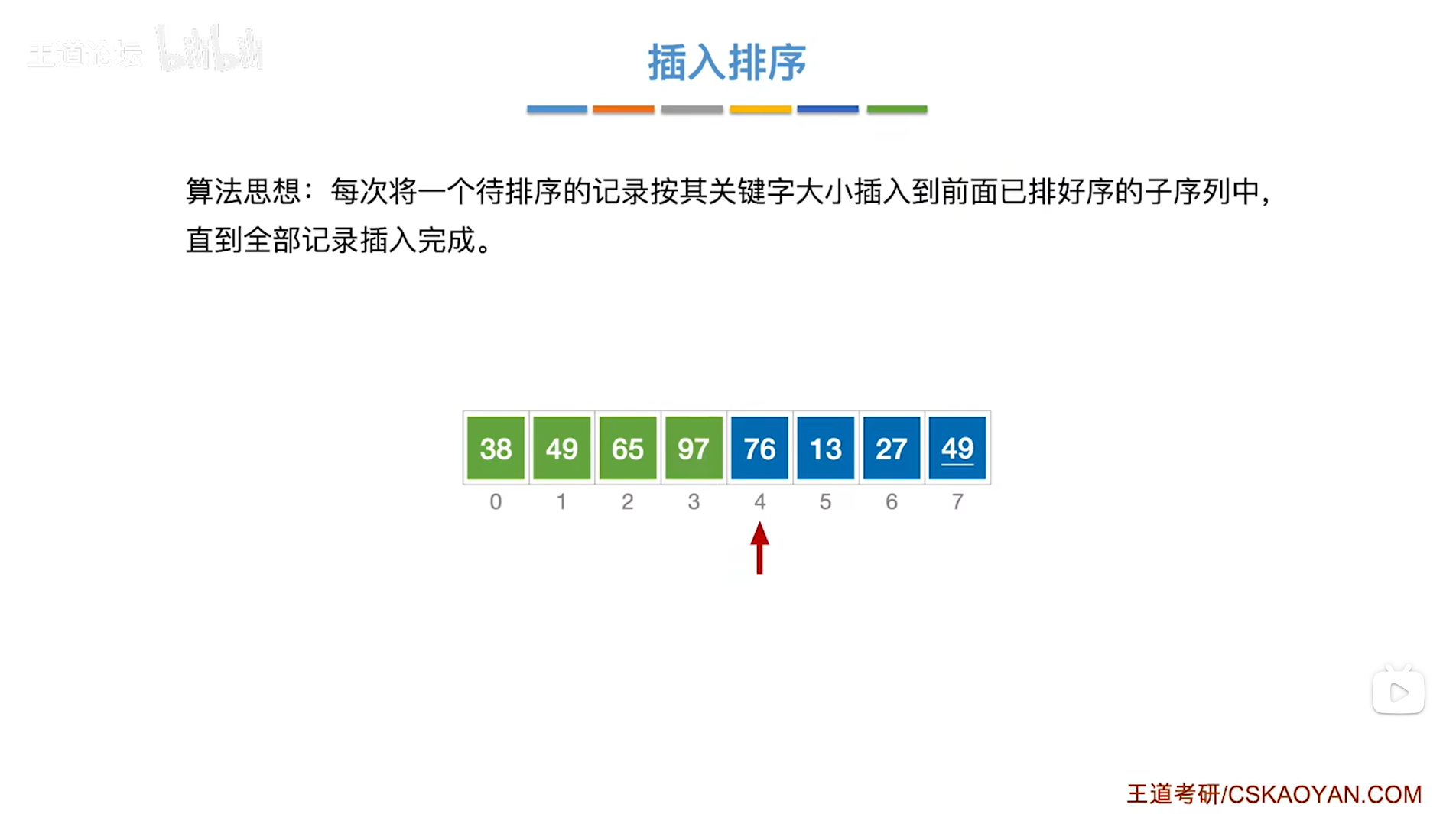
如上图，

接下来要从第五个元素即4索引上的76入手，

76需要与76前面已经排好序的元素依次进行对比，把比76大的元素都依次后移，

76前面已排好序的子序列依次为38、49、65、97，

由于76小于97，所以要把76和97互换位置，

如下图：

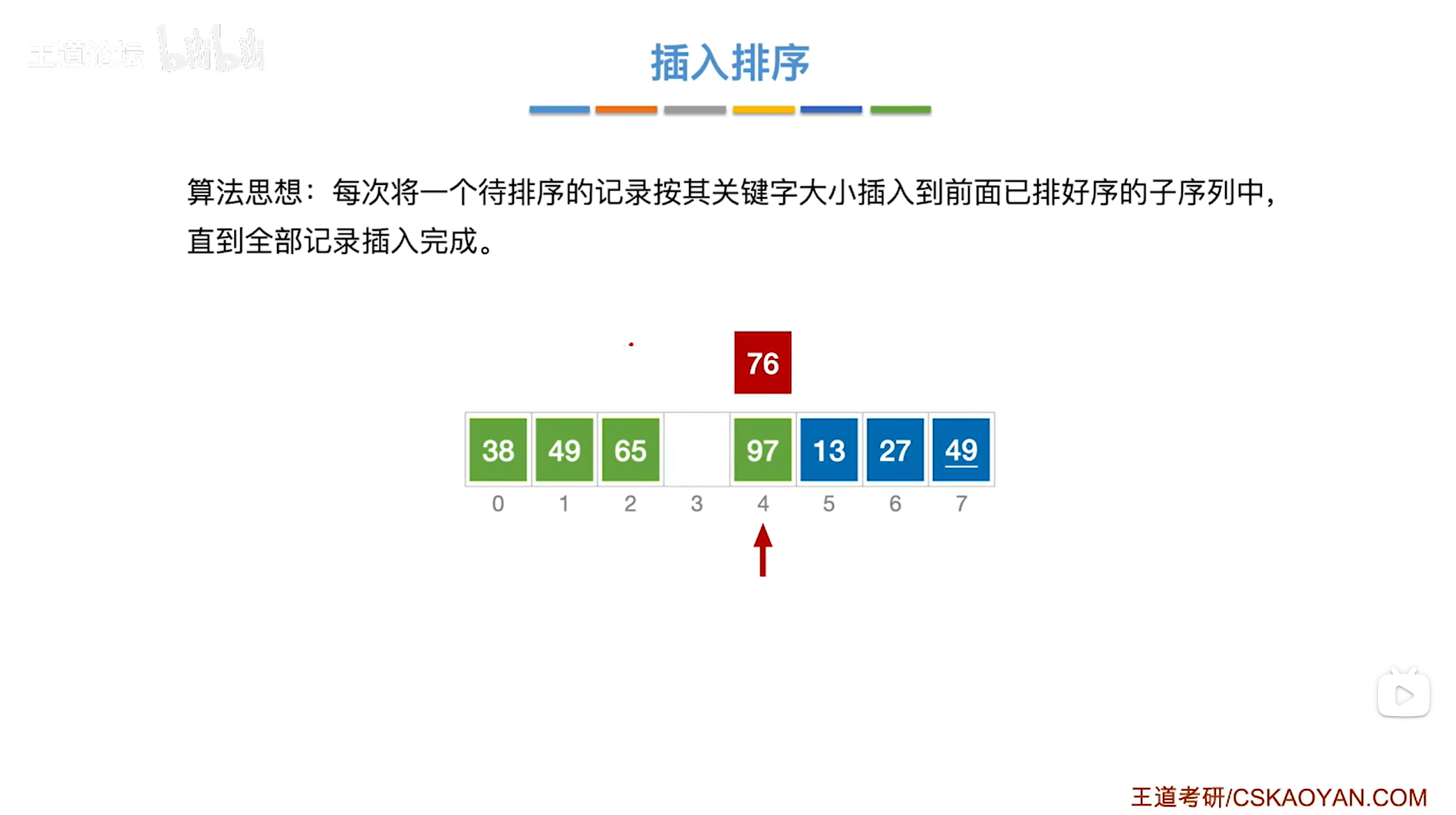
如上图，

由于76大于65，所以要把76和65无需互换位置（其实这一步就可以确定76是无需移动了，因为76已经比前面的子序列里最大的元素65大了，所以97比整个子序列大，自然就无需移动了，注：子序列是递增排序的），

至此，处理完毕，

如下图：

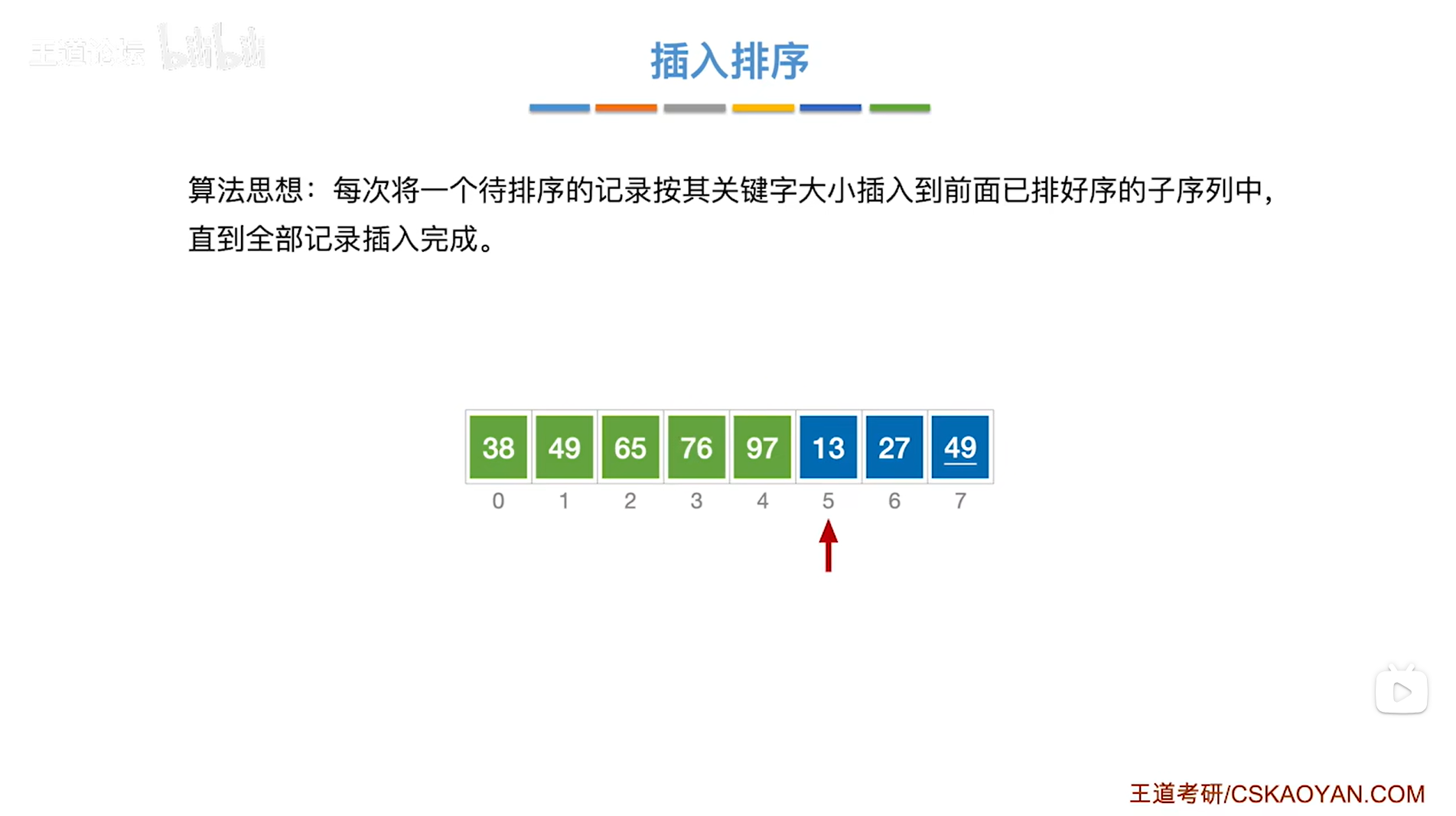
如上图，

接下来要从第六个元素即5索引上的13入手，

13需要与13前面已经排好序的元素依次进行对比，把比13大的元素都依次后移，

13前面已排好序的子序列依次为38、49、65、76、97，

由于13小于97，所以要把13和97互换位置，

如下图：

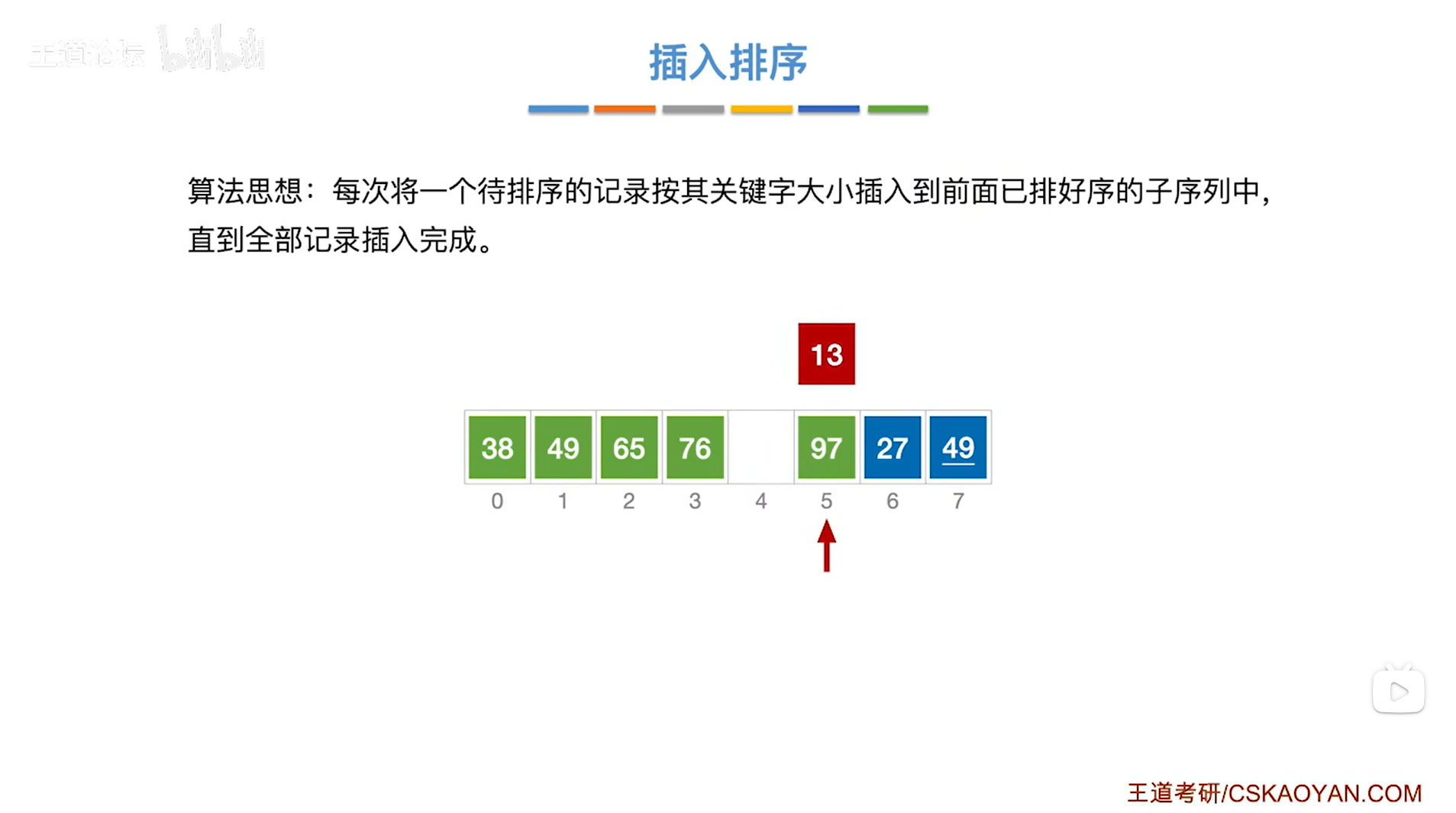
如上图，

以此类推，

最终要把13和38互换位置，

如下图：

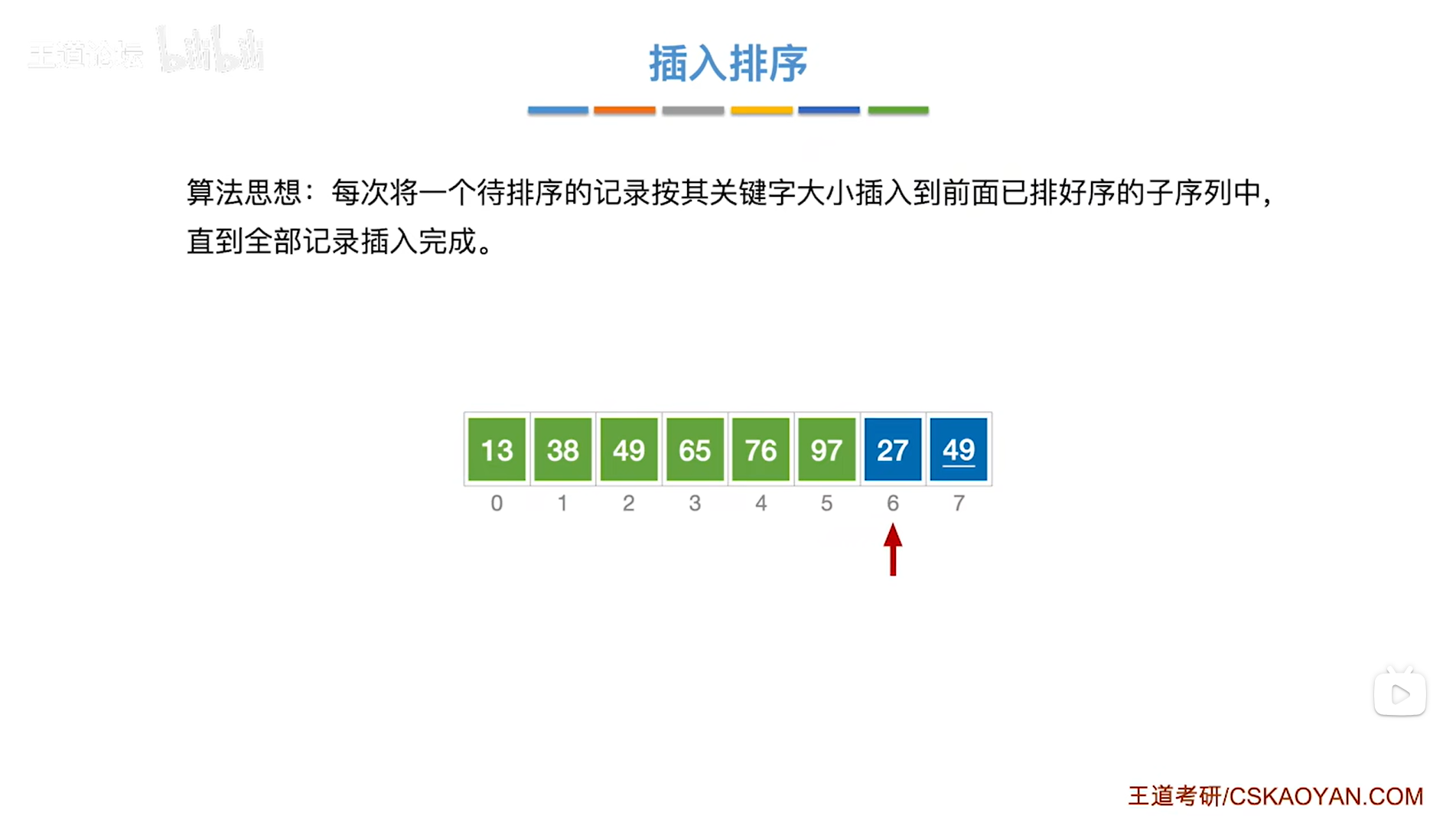
如上图，

接下来要从第七个元素即6索引上的27入手，

27需要与27前面已经排好序的元素依次进行对比，把比27大的元素都依次后移，

27前面已排好序的子序列依次为13、38、49、65、76、97，

由于27小于97，所以要把27和97互换位置，

依次类推，要把比27大的元素都往后移，

如下图：

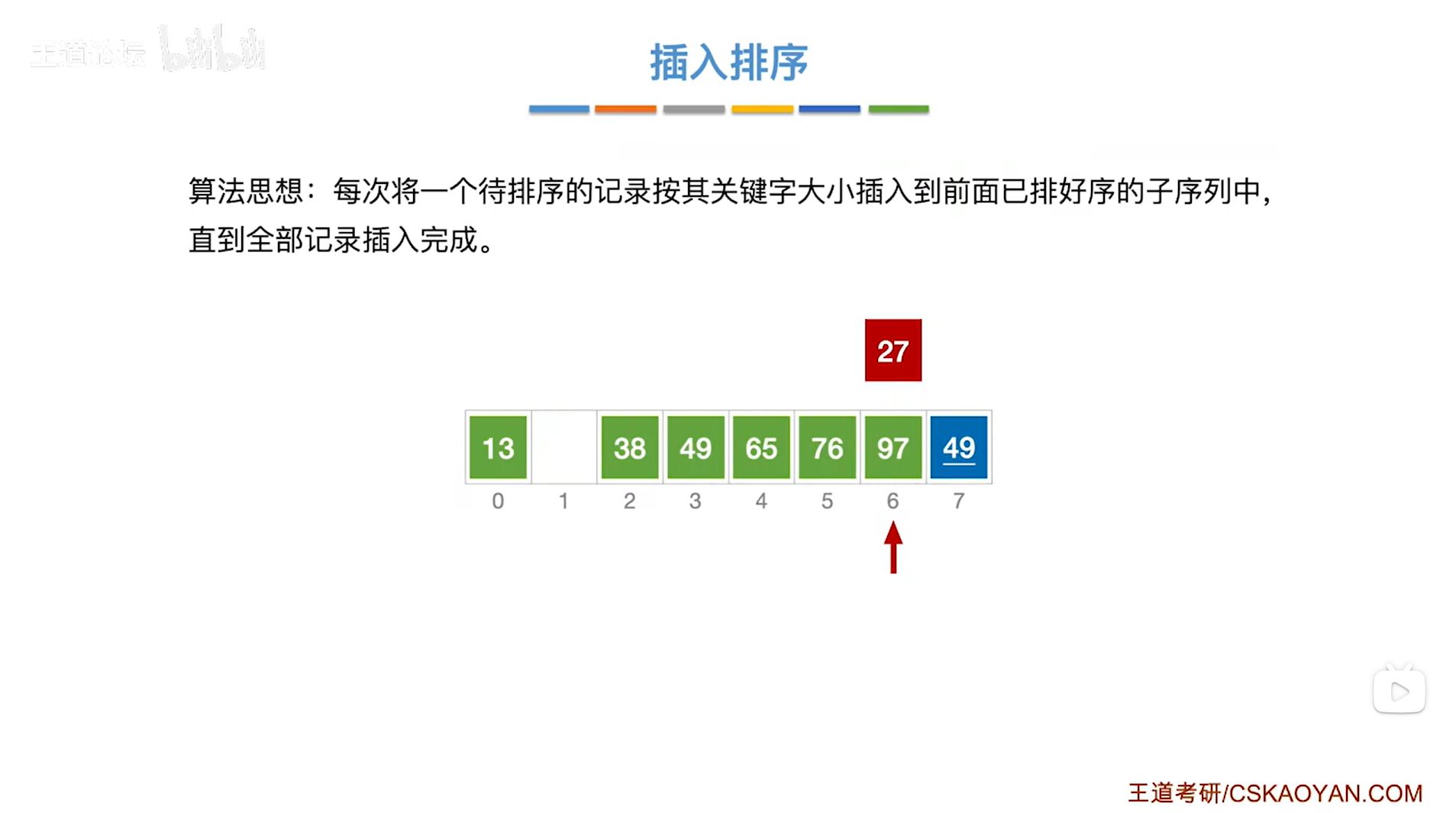
如上图，

易知最终27被换到1索引的位置，

如下图：

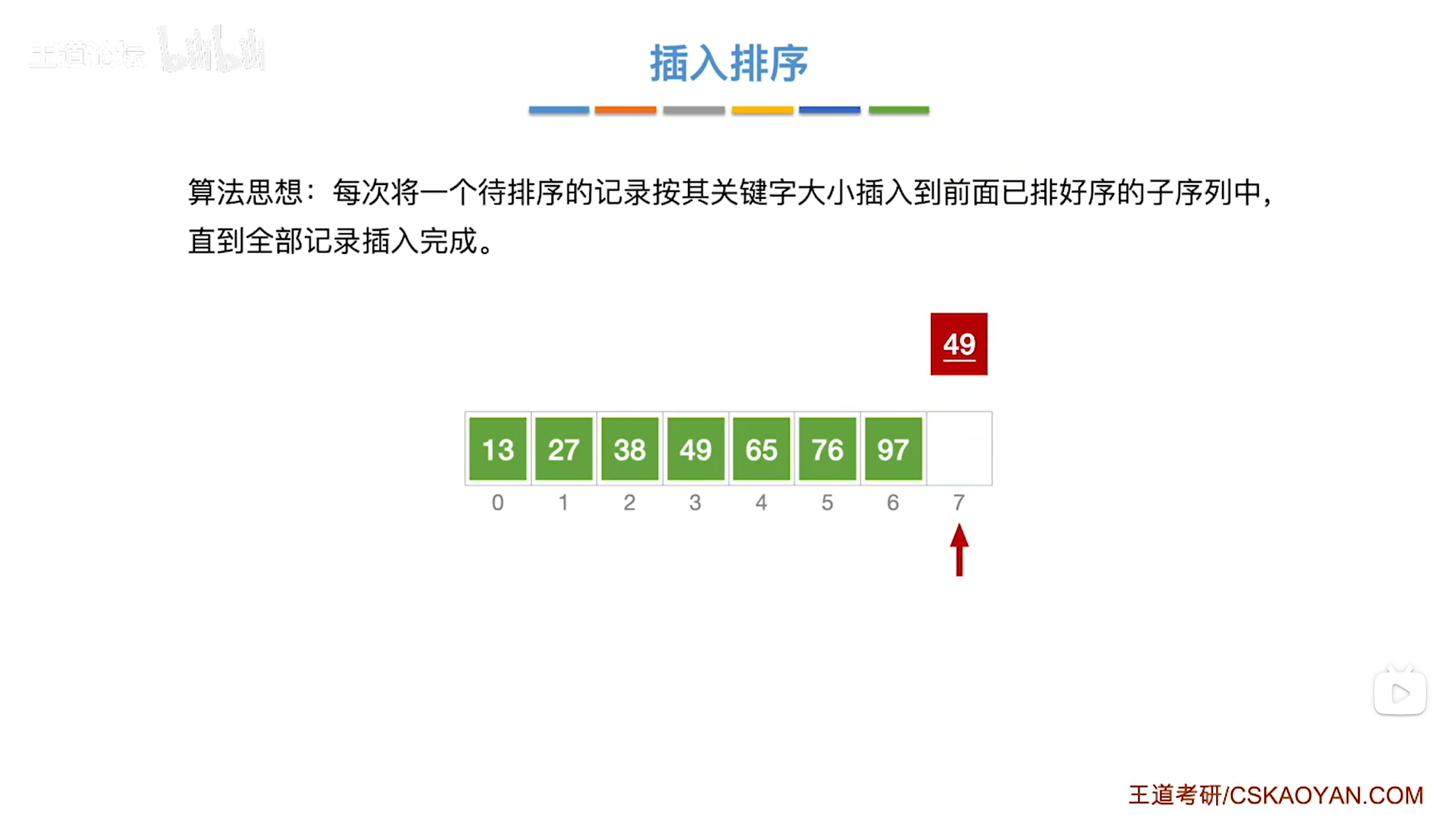
如上图，

接下来要从第八个元素即7索引上的49入手，

注：这里7索引上的49有一个下划线，是为了和3索引上的49做区分，

处理的方式和之前一样，

7索引上的49需要与7索引上的49前面已经排好序的元素依次进行对比，把比7索引上的49大的元素都依次后移，

7索引上的49前面已排好序的子序列依次为13、27、38、49、65、76、97，

由于7索引上的49小于97，所以要把7索引上的49和97互换位置，

依次类推，要把比7索引上的49大的元素都往后移，

如下图：

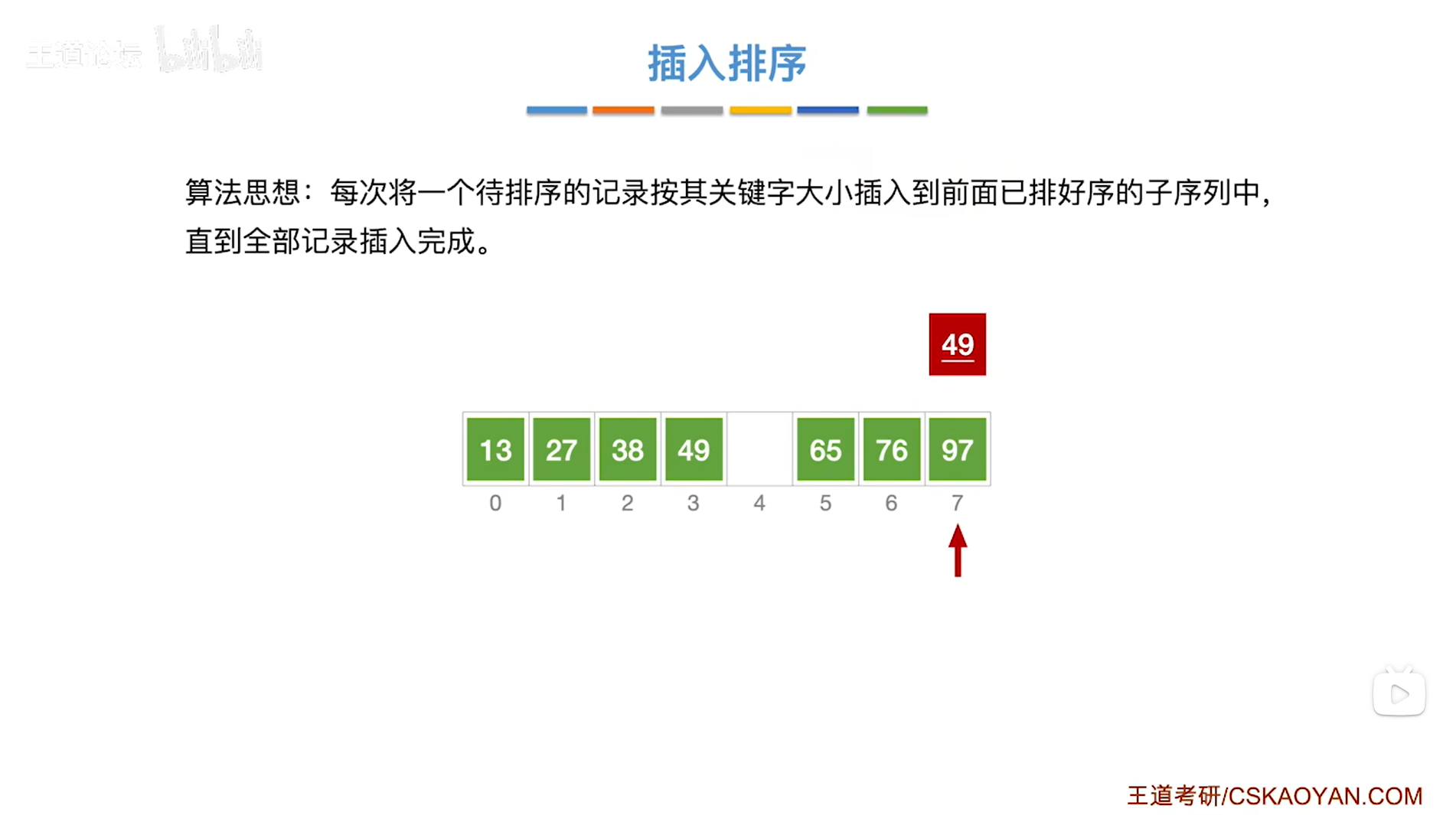
如上图，

易知最终7索引上的49被换到4索引的位置，

如下图：

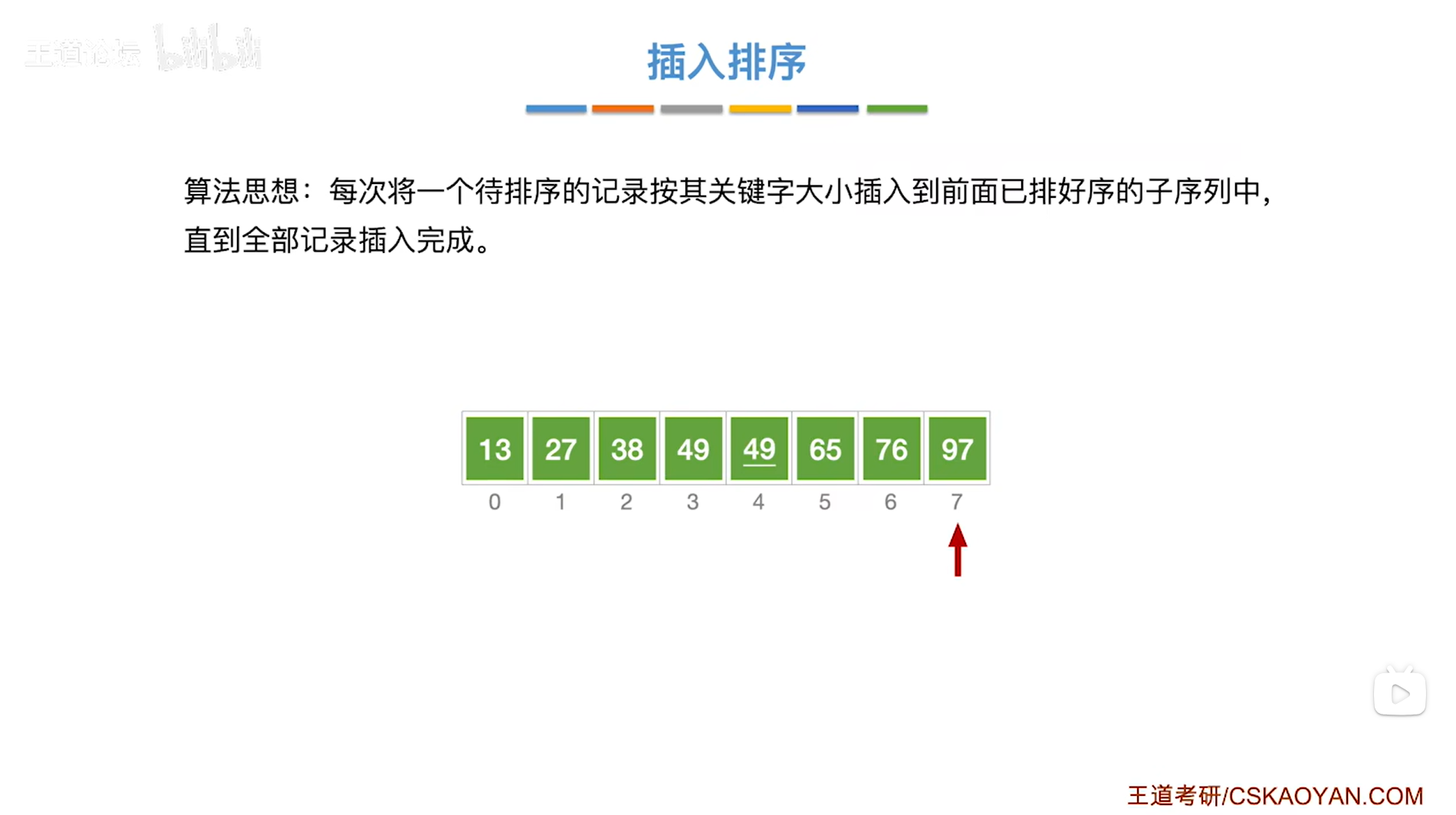
如上图，

刚才只是把比7索引上的49大的元素往后移，和7索引上的49相等的3索引上的49是没有后移的，这么做可以保证算法的稳定性。

---

三.算法实现(代码实现)：

1.方法一：换位思想

#include<stdio.h>
​
//直接插入排序->此时按照递增排序 
void InsertSort(int A[],int n) //A数组是要进行插入排序的数组，n是要参与排序的元素个数 
{
    //1.定义变量 
    int i,j,temp,index;
    //2.最外层循环用于从1索引上的元素出发，依次处理A数组里的元素 
    for(i=1 ; i<n ; i++)
    {
        /*3.当前i索引上的元素首先要和i-1索引上的元素作比较，因为i索引前的子序列是有序的，
          且按照递增排序，比较i-1索引上的元素往往可以优先判断出i索引上的元素和子序列哪个大 */
        if(A[i]<A[i-1])
        {
            //4.走if语句代表i索引上的元素小于i-1索引上的元素，要进行换位 
            /*注：只要发现A[i]<A[i-1]就必须把i索引前的每一个元素都进行比较才能找全哪些元素需要换位，
              因为一开始出现A[i]<A[i-1]，可能在更靠前的序列里也存在需要换位的元素*/
            /*5.用index记录i，因为现在要开始操作i索引上的元素进行换位，其中可能导致i的值发生改变，
              i的值改变后可能导致最外层循环进行多次，使得时间复杂度变高，
              所以用index记录i，i需要修改的地方就用index代替  */
            index=i;
            /*6.用变量temp记录i索引上的元素，因为i索引上的元素要参与换位，
                temp记录的是要实现插入序列里的元素，因此不能改变*/ 
            temp=A[index];
            /*7.现在把i-1索引记录为j，从j索引开始，最多操作完0索引结束，循环判断哪些元素需要换位；
                由于子序列是递增排序，所以当j索引上的元素小于等于temp时就停止后移，最多j操作完0索引上的元素停止
                所以循环的条件是j>=0且j索引上的元素大于temp；
                进入下一轮循环需要j-- */
            for(j=index-1; j>=0 && A[j]>temp; j--)
            {
                //8.进入循环意味着要换位
                //8.1.首先把j索引上的元素换到index索引上，此时腾出j位置 
                A[index] = A[j];
                //8.2.再把要插入的元素放到j位置上 
                A[j] = temp;
                /*8.3.进入下一轮循环时j索引要向前移一位，
                      因此index索引也需要向前移一位，
                      因为处理的就是index索引上的元素和它的前一位j索引上的元素 */
                index--;
            } 
        }
    }
} 
​
int main()
{
    return 0;
}

2.方法二：腾位置思想

#include<stdio.h>
​
//直接插入排序->此时按照递增排序
void InsertSort(int A[],int n) //A数组是要进行插入排序的数组(A数组类型不固定，因题而异)，n是要参与排序的元素个数 
{
    int i,j,temp; //变量i记录当前需要插入到前面序列的元素 
    for(i=1;i<n;i++)  //将各元素插入已经排好序的序列中 
    {
        if(A[i]<A[i-1]) //若A[i]关键字小于前驱 
        {
            temp=A[i]; //用temp暂存A[i]，防止移动元素的时候把A[i]覆盖 
            for(j=i-1;j>=0 && A[j]>temp;--j) //检查所有前面已经排好序的元素 
            {
                A[j+1] = A[j]; //所有大于temp的元素都向后挪位 
            }
            A[j+1] = temp; //正常来说是要插入到j位置，但执行完里层for循环是j-1，所以要赋值到插入位置j+1->比如要插入到2索引上，执行完for循环是2-1为1索引，因此要加1 
        }
    }
} 
​
int main()
{
    return 0;
}

3.方法三：带哨兵->数据元素从数组的1索引上开始存储，0索引不存任何数据元素来作为哨兵

#include<stdio.h>
​
//直接插入排序(带哨兵)->此时按照递增排序
void InsertSort(int A[],int n)
{
    int i,j;
    for(i=2;i<=n;i++) //依次将A[2]~A[n]插入到前面已排序序列(为什么到A[n],main函数里的例子可以解释) 
    {
        if(A[i]<A[i-1]) //若A[i]的关键字小于其前驱，那么将A[i]插入前面的序列 
        {
            A[0]=A[i]; //A[0]作为哨兵不存放元素，此时可以把A[i]即要插入的元素赋值给A[0] 
            for(j=i-1;A[0]<A[j];--j) //从后往前查找待插入位置 
            {
                A[j+1]=A[j]; //向后挪位 
            }
            A[j+1]=A[0]; //赋值到插入位置 
        }
    }
}
​
int main()
{
    int A[]={0,49,38,65,97,76,13,27,49}; //A数组的长度为9 
    InsertSort(A,8); //InsertSort第二个参数要传入8，因为A数组虽然长度为9，但0索引上的元素不参与排序即只有8个元素参与排序，刚好传入的8也是最后一个元素的索引 
    for(int i=0;i<9;i++) //A数组的最后一个索引为8 
    {
        printf("%d \n",A[i]); //A数组的排序结果从1索引开始，0索引是哨兵即不用管 
    } 
    return 0;
}

• 优点：不用每轮循环都判断j>=0，使得效率提升一些

之后以此类推。

---

四.算法效率分析：

1.空间复杂度：

数量级为O(1)，因为无论是哪种实现方式，只需要定义几个变量i，j，

换位的算法实现方式还需要定义变量temp、index；

腾位置的算法实现方式还需要定义变量temp；

带哨兵的算法实现方式会把数组0索引的位置空出来作为算法执行的辅助空间，

所有的辅助变量所需要的空间都是常数级，和问题规模即参与排序的元素个数n无关。

2.时间复杂度：

假设有n个元素参与排序，

在进行插入排序时，都是从第二个元素开始依次往后处理(带哨兵的算法虽然从2索引开始，但0索引没实际意义，从1索引开始存数据，所以2索引相当于第二个元素)，每一个元素都需要进行最外层for循环，

所以总体来看，总共需要处理n-1个元素即进行n-1趟的处理，

每一趟的处理都需要进行关键字的对比即if语句判断，甚至可能进行移动元素以及for循环里的关键字的对比，

因此时间复杂度的主要开销来自于关键字的对比和移动元素，

Ⅰ.最好的情况：原本为有序(不需要移动任何一个元素)

如上图，

如果数组中一开始各个元素就是有序排列的，这种情况下每一趟的处理都只需要进行一次关键字的对比即if语句判断，不需要进行移动元素，

所以总共n-1趟的处理，只需要进行n-1次关键字的对比即if语句判断，因此最好的时间复杂度为O(n)。

Ⅱ.最坏的情况：原本为逆序(每一个元素都需要移动)

如上图，以带哨兵的算法实现方式为例，

如果数组中一开始各个元素是逆序排列的，

这种情况下每一趟的处理中，都需要把当前i索引上的元素和i索引之前已经排好序的元素依次进行关键字的对比，

并且把之前已经排好序的元素全部都后移1位，意味着if语句和里层for循环都要进行。

比如处理i索引上的元素，意味着进行到第i-1趟（例如处理2索引上的元素就是第1趟），

首先进行if语句中A[i]<A[i-1]判断->本操作中关键字对比1次；

再执行A[0]=A[i]，把第i索引上的元素即当前操作的元素移位到0索引上->本操作中移动元素1次；

再执行里层for循环，由于此时是逆序，所以会进行到底即处理到j为1索引上的元素，这里需要i-1次关键字的对比即A[0]<A[j]，和i-1次移位->本操作中关键字对比i-1次，移动元素i-1次；

最后执行A[j+1]=A[0]，把要插入的元素移位到所要插入的位置->本操作中移动元素1次，

综上，第i-1趟总共要关键字对比1+(i-1)即i次，移动元素1+(i-1)+1即i+1次，

所以第i趟总共要关键字对比i+1次，移动元素i+2次，

如下图：

如上图，

当进行到最后一趟排序时，要处理的是关键字10，需进行if语句判断后把当前要处理的关键字10移动到0索引上，接下来的for循环还需要把关键字10和前面已经排好序的所有的元素都进行一次关键字的对比，并且要把这些元素都依次后移1位，再把关键字10插入到第一位，

根据"第i趟总共要关键字对比第i+1次，移动元素i+2次"，如果要对比n趟，总共需要对比关键字2+3+...+(n+1)=(n²+3n)/2次，移动元素3+4+...+(n+2)=(n²+5n)/2次，

由于对比关键字和移动元素这两个操作是并列进行(不是嵌套)，所以将这两个操作的数量级相加就会达到O( (n²+3n)/2 + (n²+5n)/2 )，等价于O(n²)，

因此最坏的时间复杂度为O(n²)。

3.总结：

插入排序最好的时间复杂度为O(n)，最坏的时间复杂度为O(n²)，

因此插入排序的平均时间复杂度为O( (n+n²)/2 )，等价于O(n²)，

插入排序显然是稳定的排序算法。

---

五.优化-折半插入排序：

1.优化思想：

如上图，

之前在处理某一个元素的时候，都是用顺序查找的方式依次往前找当前处理的元素应插入的位置，

但是由于当前处理的元素前面的序列已经是有序的，且在上述图片中的例子是用顺序存储的方式来存储，

所以可以使用折半查找的方式来更快地找到当前处理的元素应插入的位置。

2.实例：

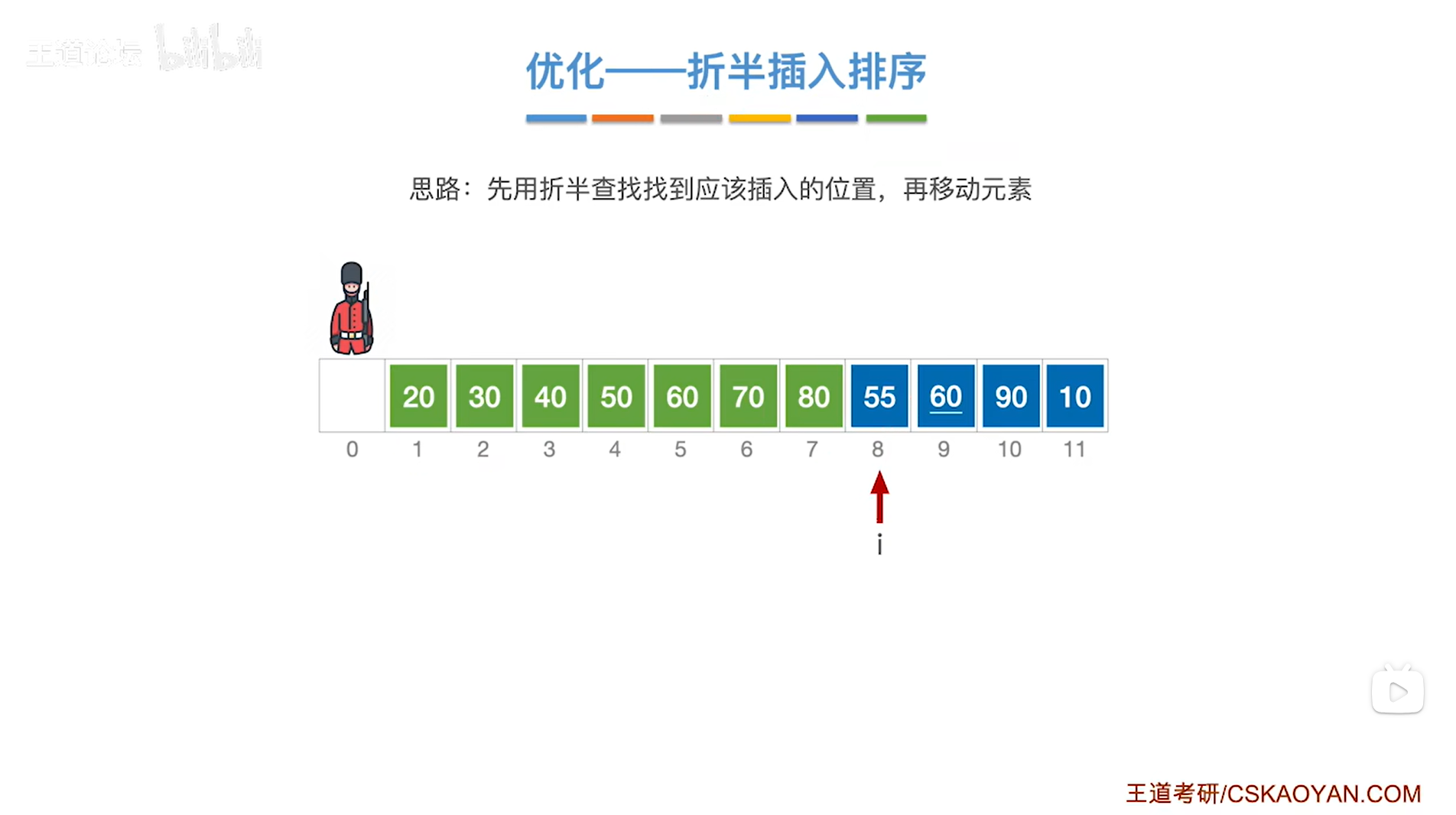
以上述图片为例，

采取带哨兵的算法实现方式，且按照递增方式排序，

如下图：

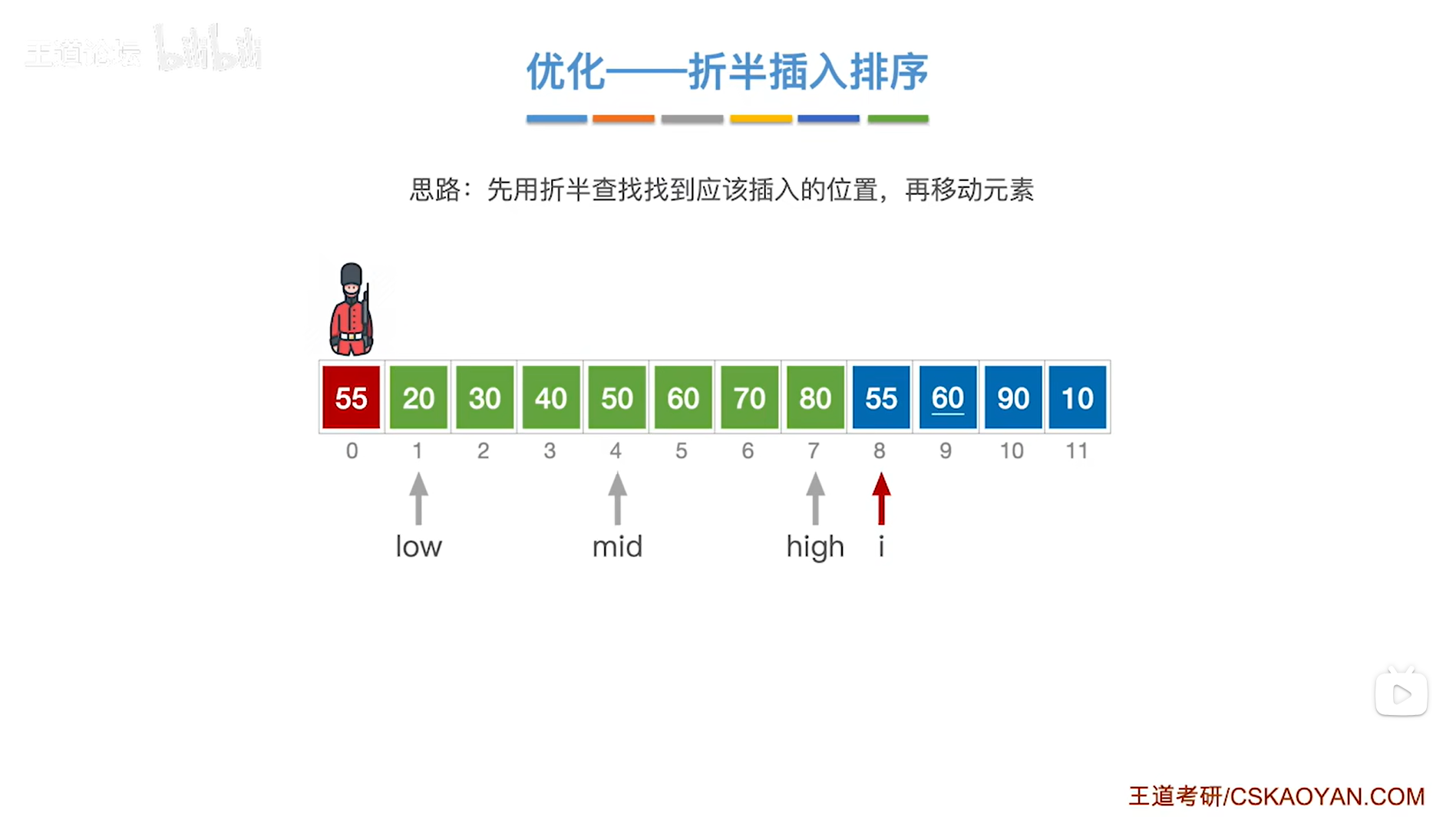
如上图，

如果现在处理到8索引上的元素55，

首先在A[0]的位置把当前处理的元素55保存下来，防止它被覆盖，

接下来在当前处理的元素55前面的序列内找出它应该插入的位置，

初始时low指针指向1索引即low为1，意味着low指针指向序列的第一个元素20；

high指针指向7索引即high为7，意味着high指针指向序列的最后一个元素80，

通过mid = ( low + high ) / 2可得出中间指针mid为4，因此中间指针mid指向4索引，意味着中间指针mid指向序列中4索引上的元素50；

中间指针mid指向的元素50小于当前处理的元素55，

由于要按照递增方式排序，

所以当前处理的元素55应该插在50右边的区间内，因此接下来会在50右边的区间内进行查找当前处理的元素55应插入的位置，

low指针指向mid+1即5索引上，high指针不变即指向7索引上，

如下图：

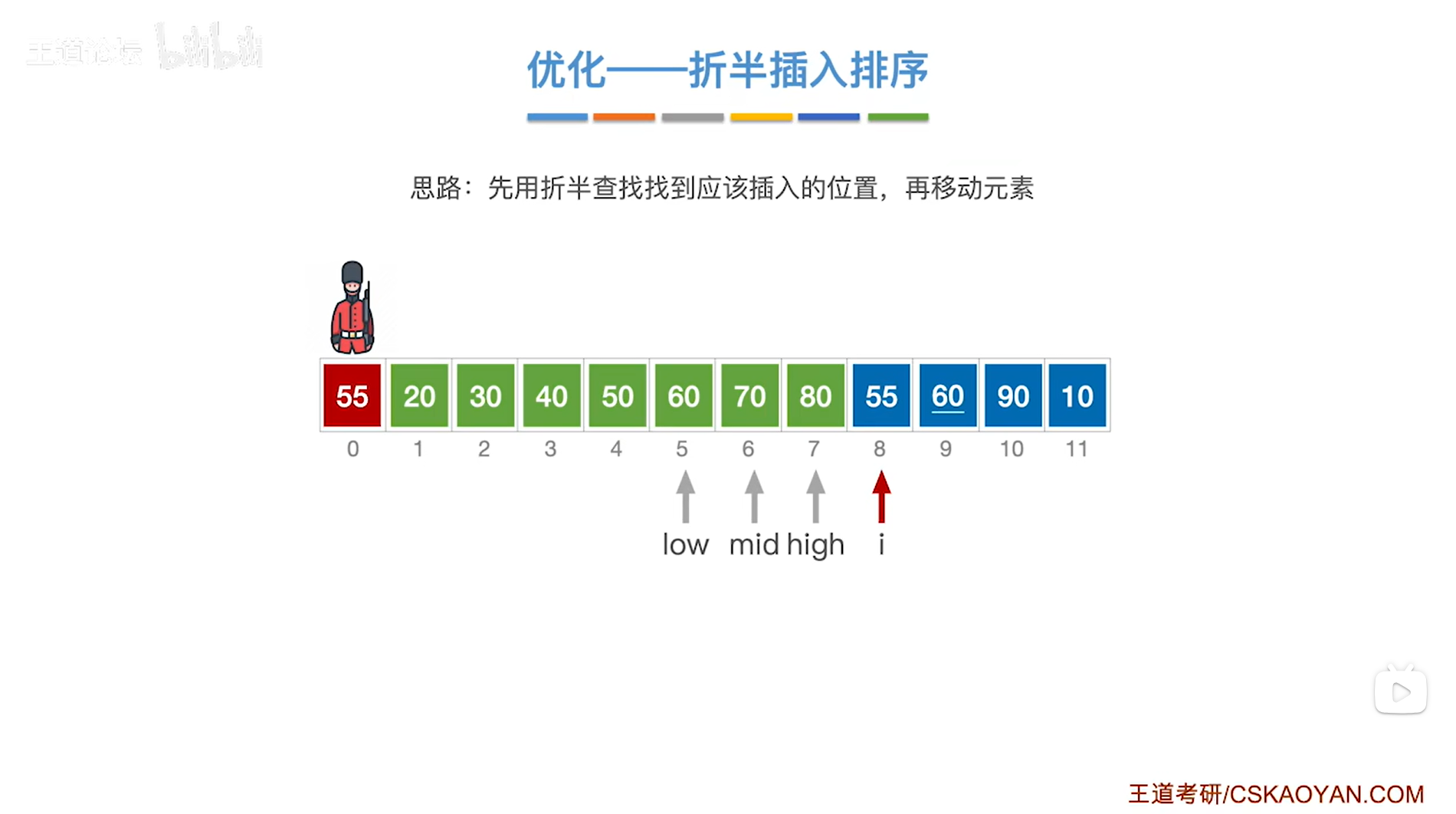
如上图，

现在low指针指向5索引即low为5，意味着low指针指向序列的第五个元素60；

high指针指向7索引即high为7，意味着high指针指向序列的第七个元素80，

通过mid = ( low + high ) / 2可得出中间指针mid为6，因此中间指针mid指向6索引，意味着中间指针mid指向序列中6索引上的元素70；

中间指针mid指向的元素70大于当前处理的元素55，

由于要按照递增方式排序，

所以当前处理的元素55应该插在70左边的区间内，因此接下来会在70左边的区间内进行查找当前处理的元素55应插入的位置，

low指针不变即指向5索引上，high指针指向mid-1即5索引上，

如下图：

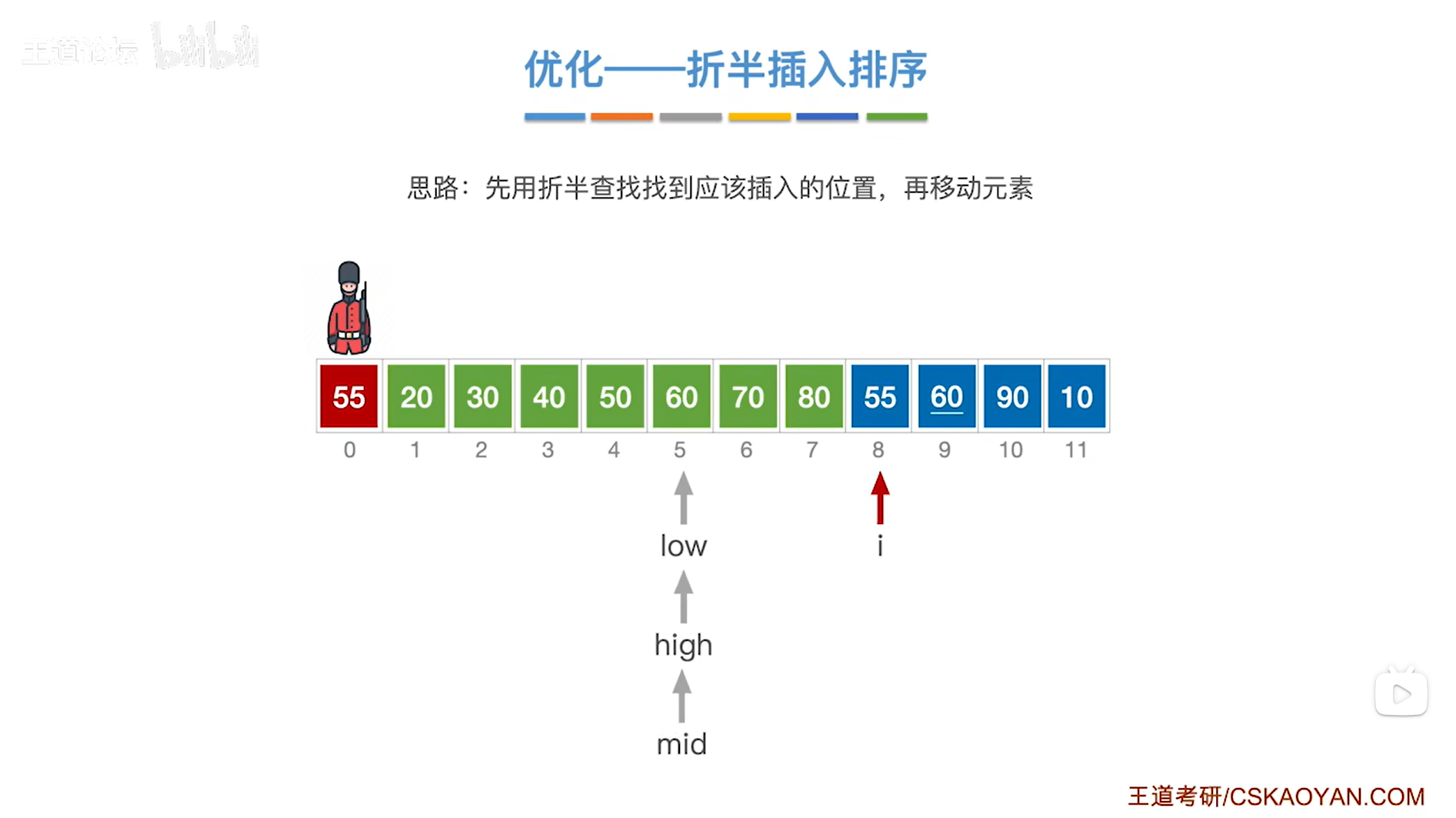
如上图，

现在low指针指向5索引即low为5，意味着low指针指向序列的第五个元素60；

high指针指向5索引即high为5，意味着high指针指向序列的第五个元素60，

通过mid = ( low + high ) / 2可得出中间指针mid为5，因此中间指针mid指向5索引，意味着中间指针mid指向序列中5索引上的元素60；

中间指针mid指向的元素60大于当前处理的元素55，

由于要按照递增方式排序，

所以当前处理的元素55应该插在60左边的区间内，因此接下来会在60左边的区间内进行查找当前处理的元素55应插入的位置，

low指针不变即指向5索引上，high指针指向mid-1即4索引上，

如下图：

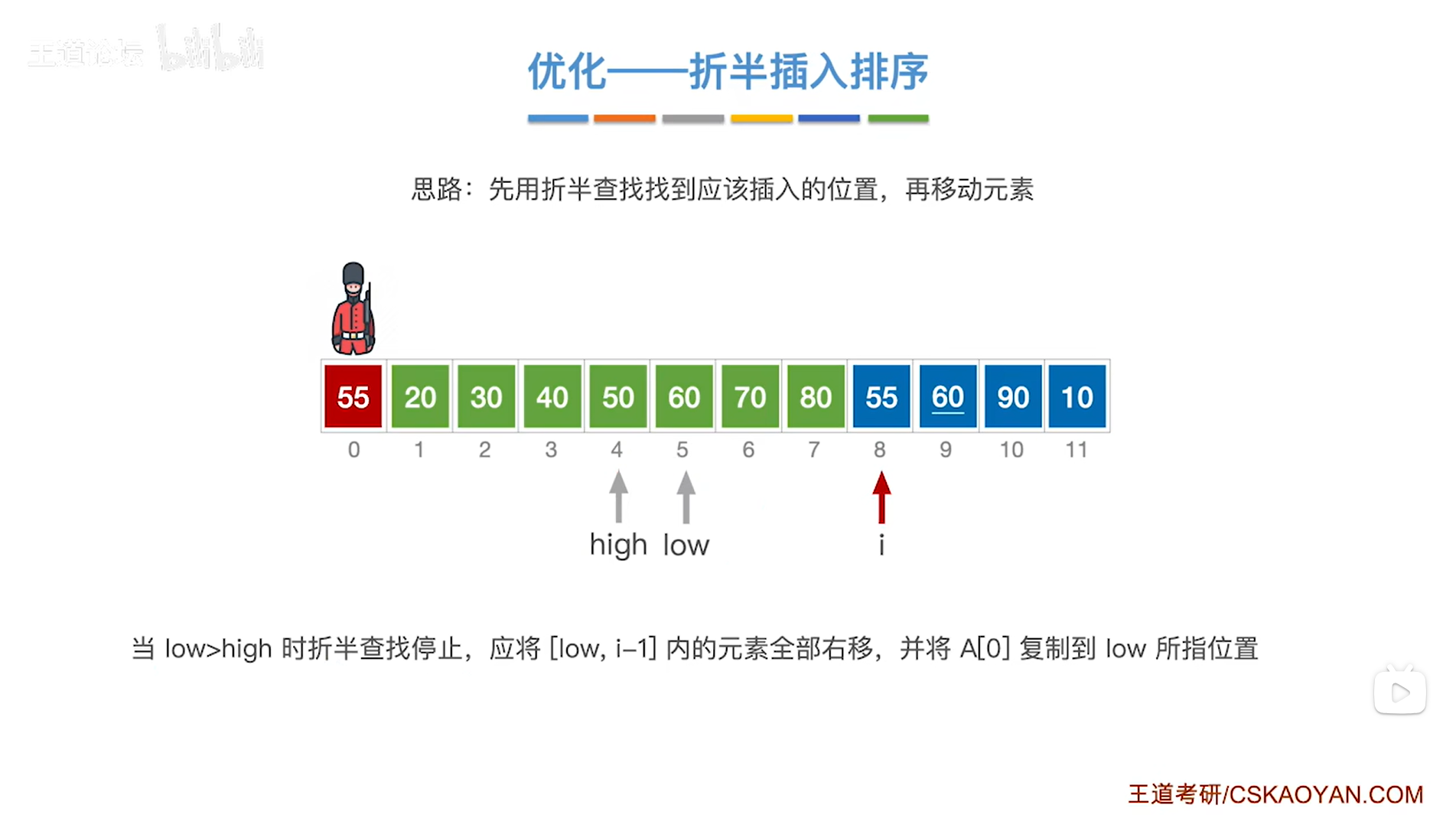
如上图，

现在low指针指向5索引即low为5，high指针指向4索引即high为4，

出现了low>high，此时就应该停止折半查找，

low指针指向的元素以及low指针右边序列内的元素即[low,i-1]序列里的元素都比当前处理的元素55更大，

所以接下来要把[low,i-1]序列内的元素全部后移，给当前处理的元素55腾出一个位置，

并将当前处理的元素55赋值到low指针所指的位置，

至此，元素55处理完毕，

如下图：

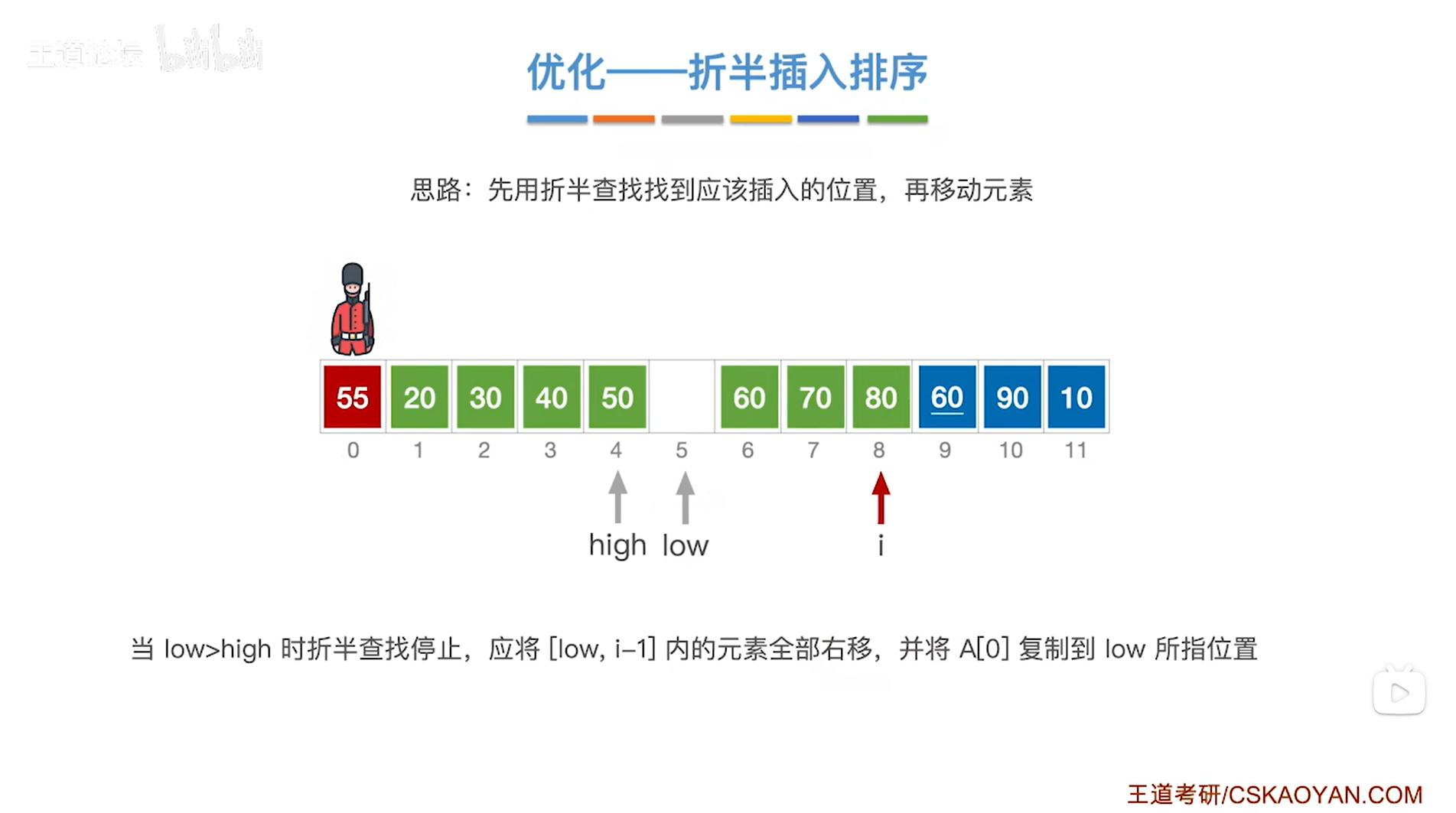
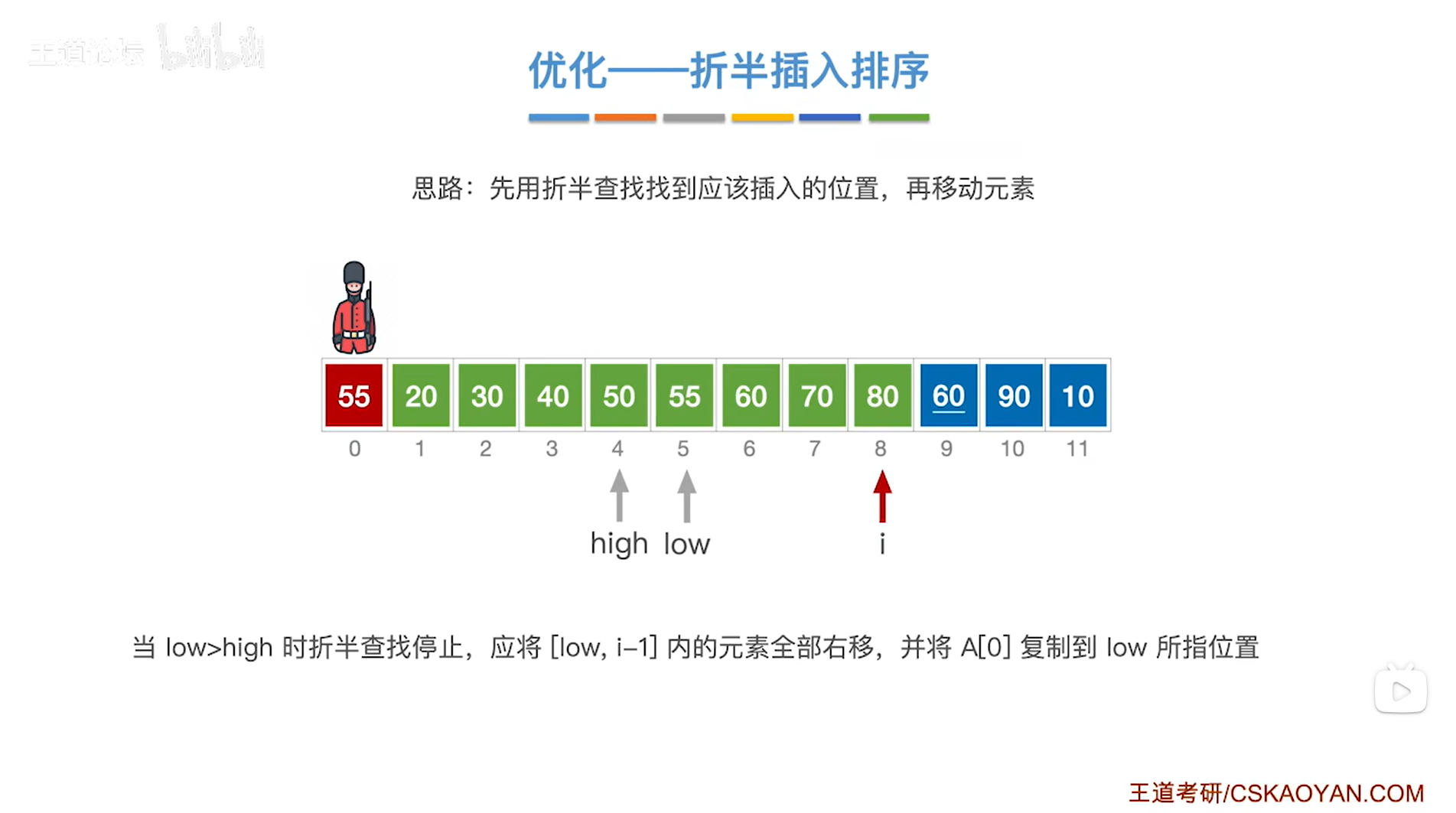
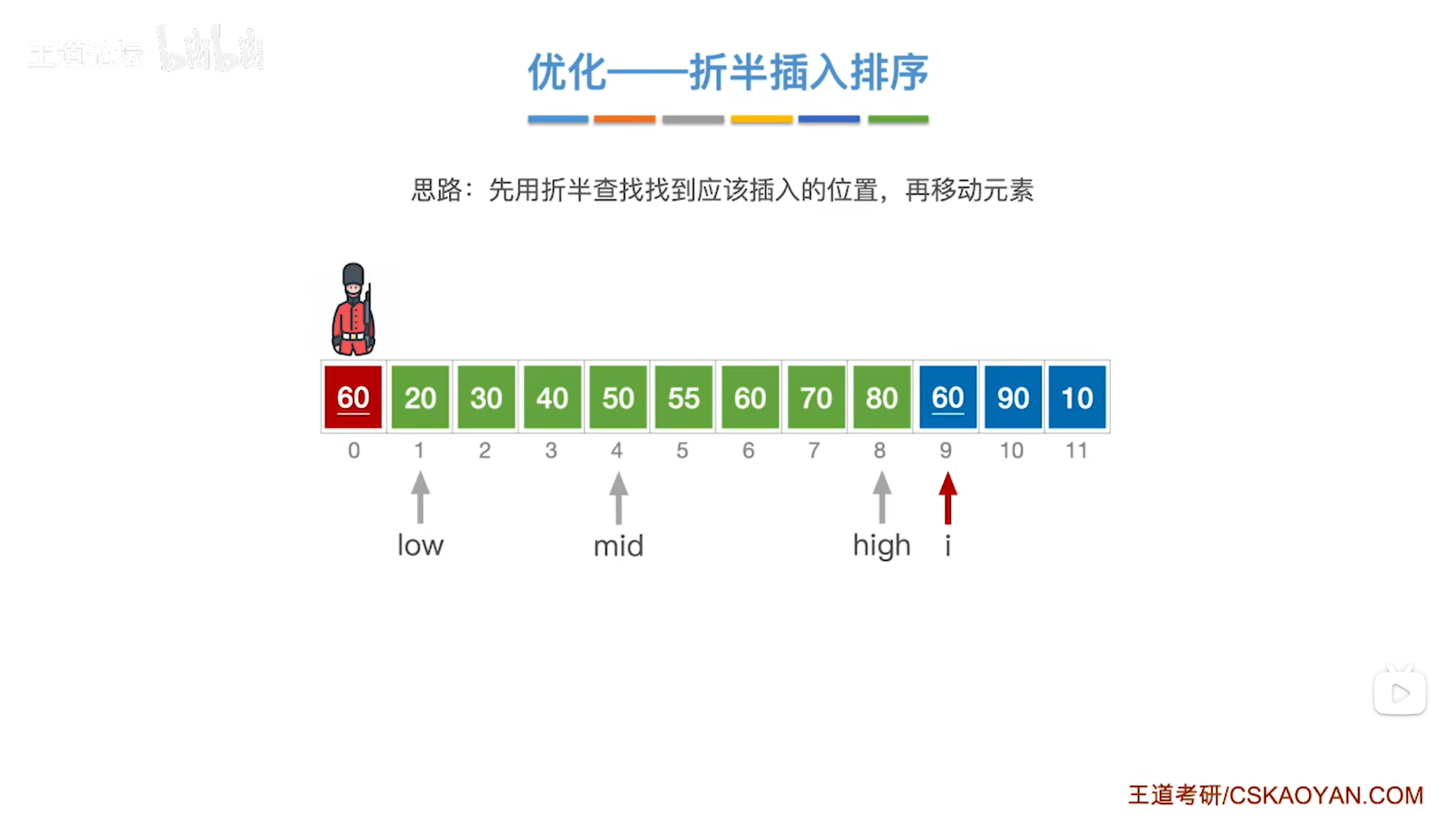
如上图，

接下来该处理9索引上的元素60，

首先在A[0]的位置把当前处理的元素60保存下来，防止它被覆盖，

接下来在当前处理的元素60前面的序列内找出它应该插入的位置，

初始时low指针指向1索引即low为1，意味着low指针指向序列的第一个元素20；

high指针指向8索引即high为8，意味着high指针指向序列的最后一个元素80，

通过mid = ( low + high ) / 2可得出中间指针mid为4，因此中间指针mid指向4索引，意味着中间指针mid指向序列中4索引上的元素50；

中间指针mid指向的元素50小于当前处理的元素60，

由于要按照递增方式排序，

所以当前处理的元素60应该插在50右边的区间内，因此接下来会在50右边的区间内进行查找当前处理的元素60应插入的位置，

low指针指向mid+1即5索引上，high指针不变即指向8索引上，

如下图：

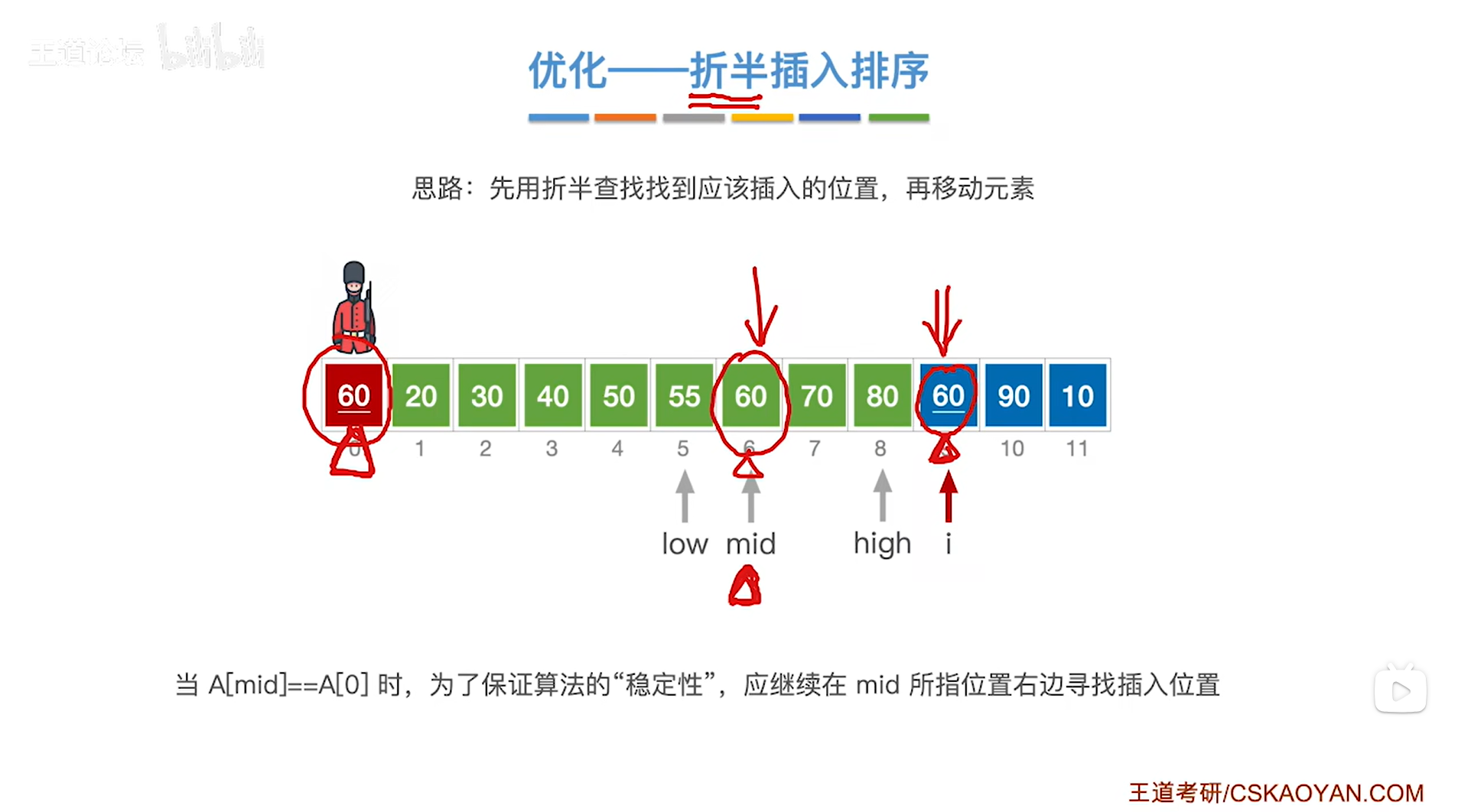
如上图，

现在low指针指向5索引即low为5，意味着low指针指向序列的第五个元素55；

high指针指向8索引即high为8，意味着high指针指向序列的第八个元素80，

通过mid = ( low + high ) / 2可得出中间指针mid为6，因此中间指针mid指向6索引，意味着中间指针mid指向序列中6索引上的元素60；

此时会发现中间指针mid指向的元素60等于当前处理的元素60，

根据之前设计的折半查找规则(详情见"7.3.折半查找(二分查找)")，当找到一个和目标关键字相等的关键字时就会停止折半查找，

但在这个地方为了保证插入排序的稳定性，且要按照递增方式排序，若发现了中间指针mid指向的元素等于当前处理的元素时，还应该继续在中间指针mid的右半区间内继续查找，来确定当前处理的元素应插入的位置，

所以当发现了中间指针mid指向的元素等于当前处理的元素时并不会让折半查找停止，而是继续在mid指针所指的位置的右区间内继续查找当前处理的元素60应该插入的位置，

因此low指针指向mid+1即7索引上，high指针不变即指向8索引上，

如下图：

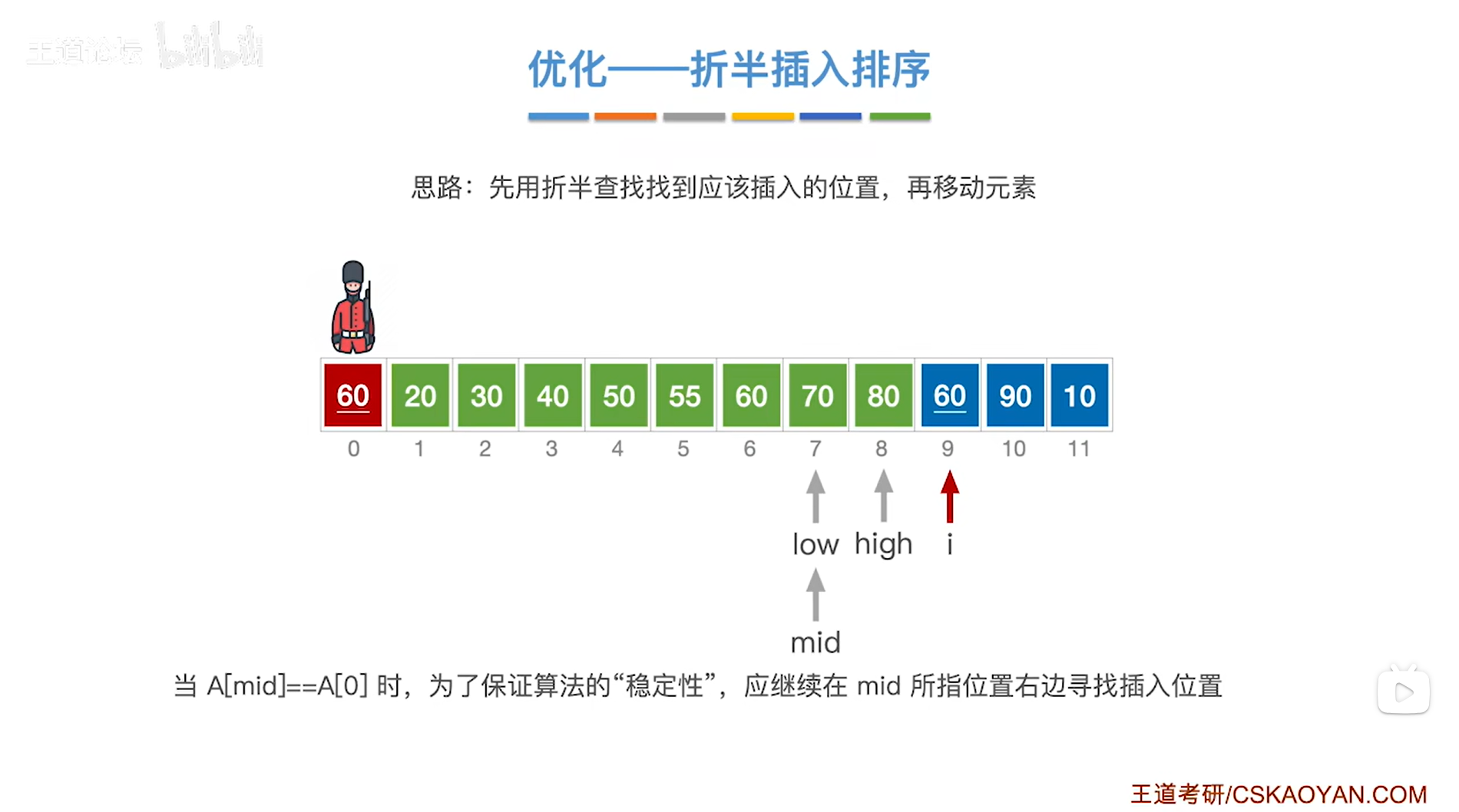
如上图，

现在low指针指向7索引即low为7，意味着low指针指向序列的第七个元素70；

high指针指向8索引即high为8，意味着high指针指向序列的第八个元素80，

通过mid = ( low + high ) / 2可得出中间指针mid为7，因此中间指针mid指向7索引，意味着中间指针mid指向序列中7索引上的元素70；

中间指针mid指向的元素70大于当前处理的元素60，

由于要按照递增方式排序，

所以当前处理的元素60应该插在70左边的区间内，因此接下来会在70左边的区间内进行查找当前处理的元素60应插入的位置，

low指针不变即指向7索引上，high指针指向mid-1即6索引上，

如下图：

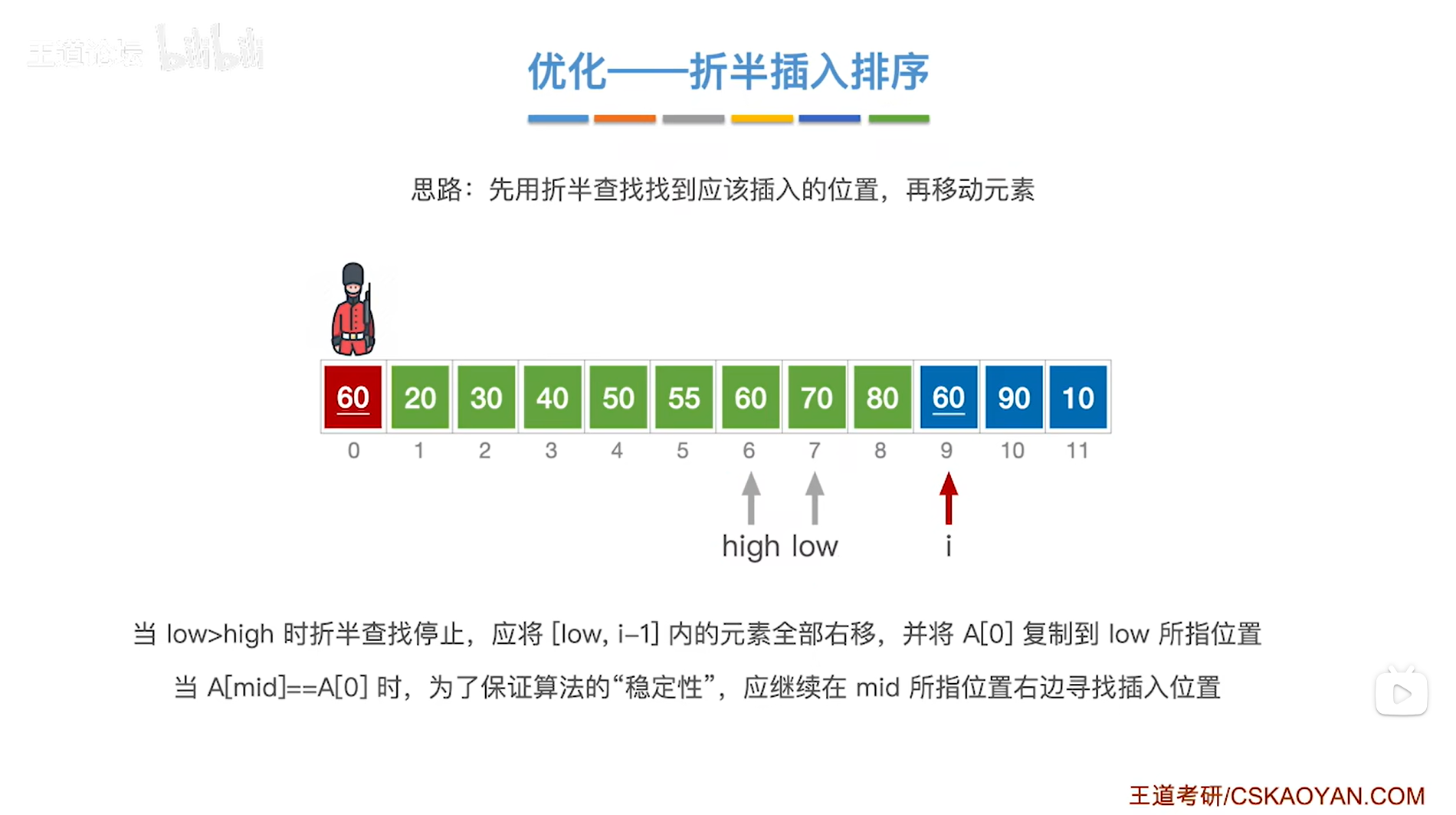
如上图，

现在low指针指向7索引即low为7，high指针指向6索引即high为6，

出现了low>high，此时就应该停止折半查找，

low指针指向的元素以及low指针右边序列内的元素即[low,i-1]序列里的元素都比当前处理的元素60更大，

所以接下来要把[low,i-1]序列内的元素全部后移，给当前处理的元素60腾出一个位置，

并将当前处理的元素60赋值到low指针所指的位置，

至此，元素60处理完毕，

如下图：

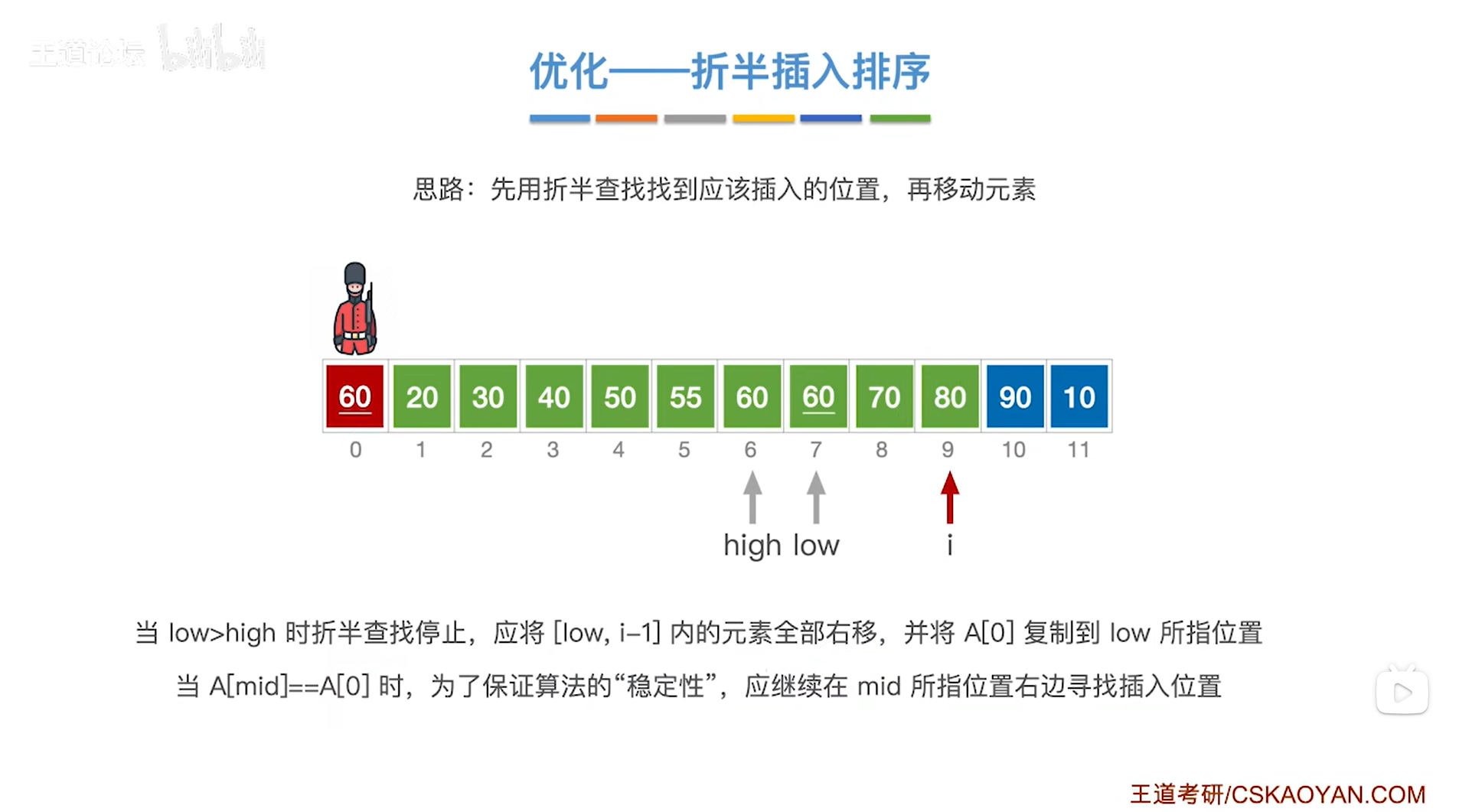
如上图，

接下来该处理10索引上的元素90，

首先在A[0]的位置把当前处理的元素90保存下来，防止它被覆盖，

接下来在当前处理的元素90前面的序列内找出它应该插入的位置，

初始时low指针指向1索引即low为1，意味着low指针指向序列的第一个元素20；

high指针指向9索引即high为9，意味着high指针指向序列的最后一个元素80，

通过mid = ( low + high ) / 2可得出中间指针mid为5，因此中间指针mid指向5索引，意味着中间指针mid指向序列中5索引上的元素55；

中间指针mid指向的元素55小于当前处理的元素90，

由于要按照递增方式排序，

所以当前处理的元素90应该插在55右边的区间内，因此接下来会在55右边的区间内进行查找当前处理的元素90应插入的位置，

low指针指向mid+1即6索引上，high指针不变即指向9索引上，

之后以此类推，

最终low指针指向10索引即low为10，high指针指向9索引即high为9，

会导致low>high，折半查找停止，

如下图：

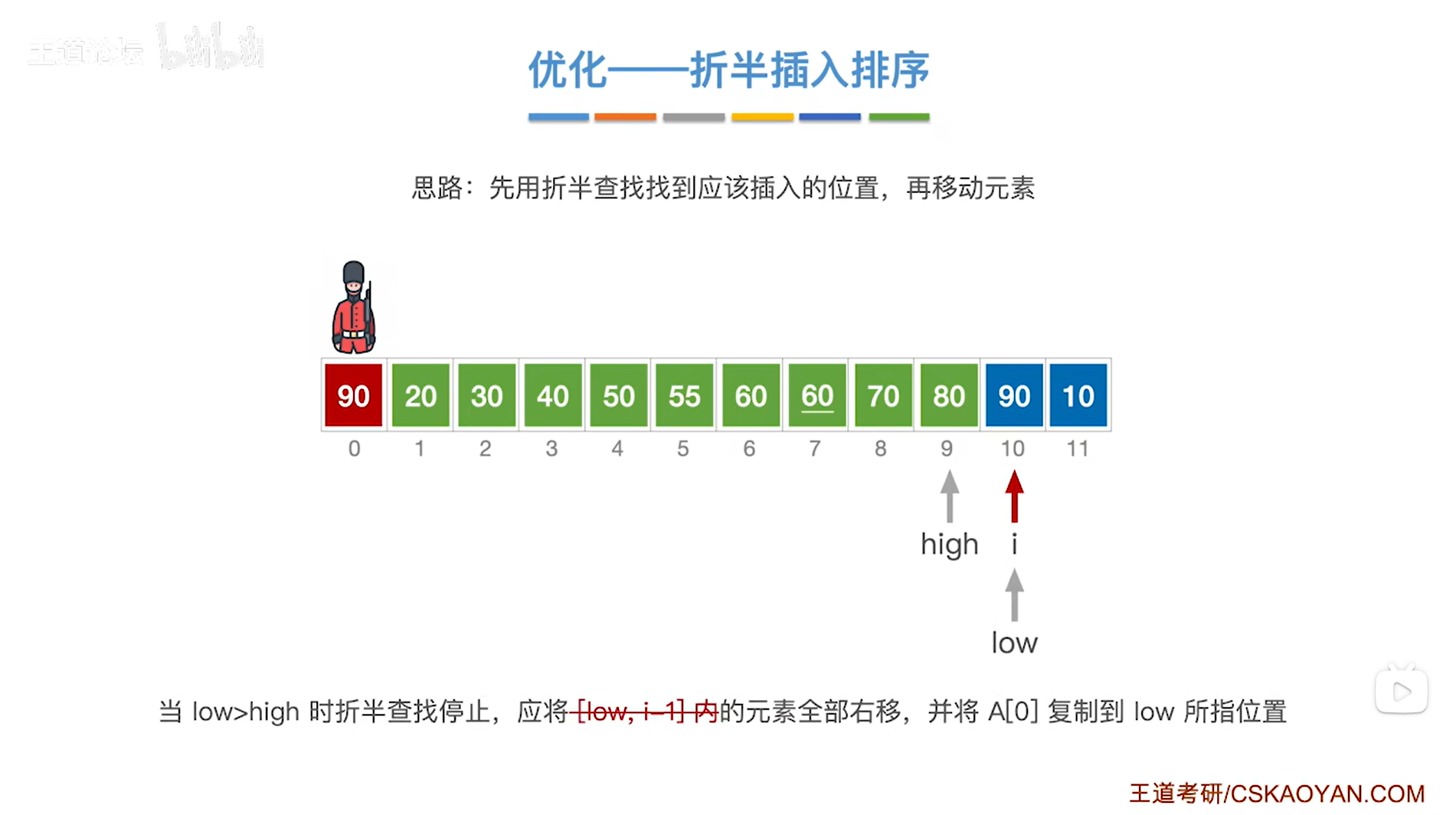
如上图，

此时出现了low>i-1即low指针超出了查找序列，

low指针指向10索引上的元素即当前处理的元素90，超出了查找序列最大索引9，

这种情况下不需要移动任何一个元素，

至此，元素90处理完毕，

如下图：

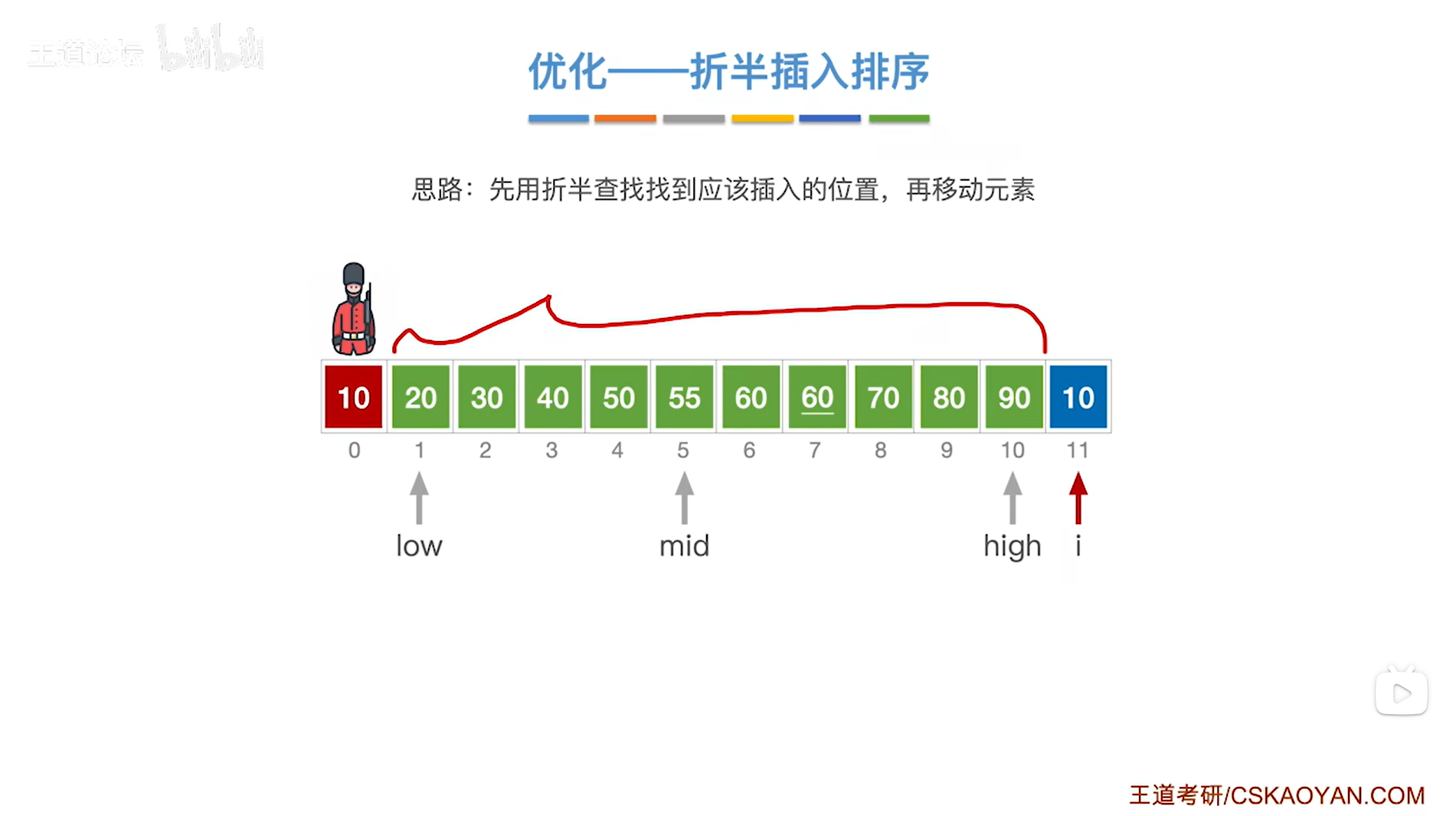
如上图，

接下来该处理11索引上的元素10，

首先在A[0]的位置把当前处理的元素10保存下来，防止它被覆盖，

接下来在当前处理的元素10前面的序列内找出它应该插入的位置，

初始时low指针指向1索引即low为1，意味着low指针指向序列的第一个元素20；

high指针指向10索引即high为10，意味着high指针指向序列的最后一个元素90，

通过mid = ( low + high ) / 2可得出中间指针mid为5，因此中间指针mid指向5索引，意味着中间指针mid指向序列中5索引上的元素55；

中间指针mid指向的元素55大于当前处理的元素10，

由于要按照递增方式排序，

所以当前处理的元素10应该插在55左边的区间内，因此接下来会在55左边的区间内进行查找当前处理的元素10应插入的位置，

low指针不变即指向1索引上，high指针指向mid-1即4索引上，

之后以此类推，

最终low指针指向1索引即low为1，high指针指向0索引即high为0，

会导致low>high，折半查找停止，

如下图：

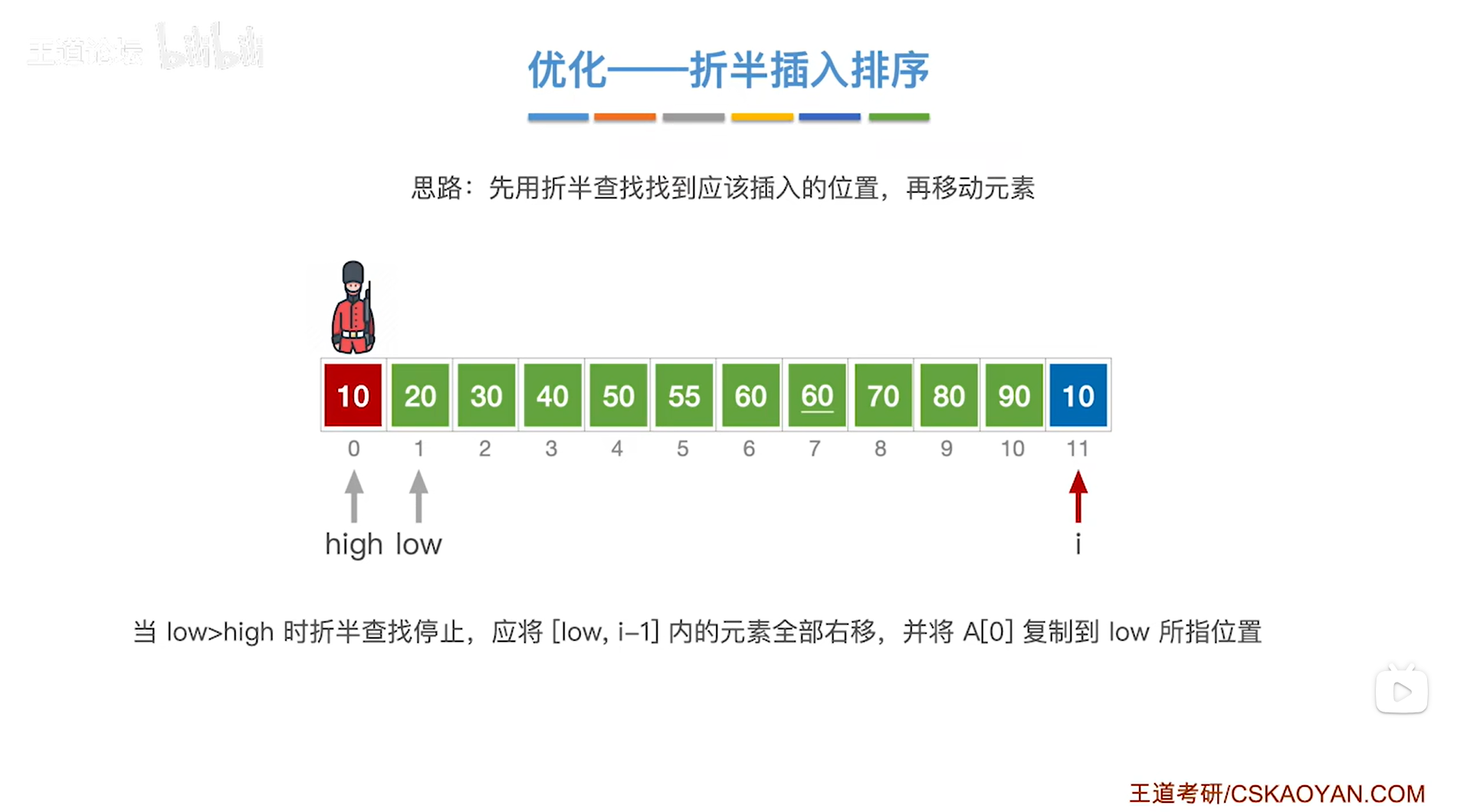
如上图，

low指针指向的元素以及low指针右边序列内的元素即[low,i-1]序列里的元素都比当前处理的元素10更大，

所以接下来要把[low,i-1]序列内的元素全部后移，给当前处理的元素10腾出一个位置，

并将当前处理的元素10赋值到low指针所指的位置，

至此，元素10处理完毕，

如下图：

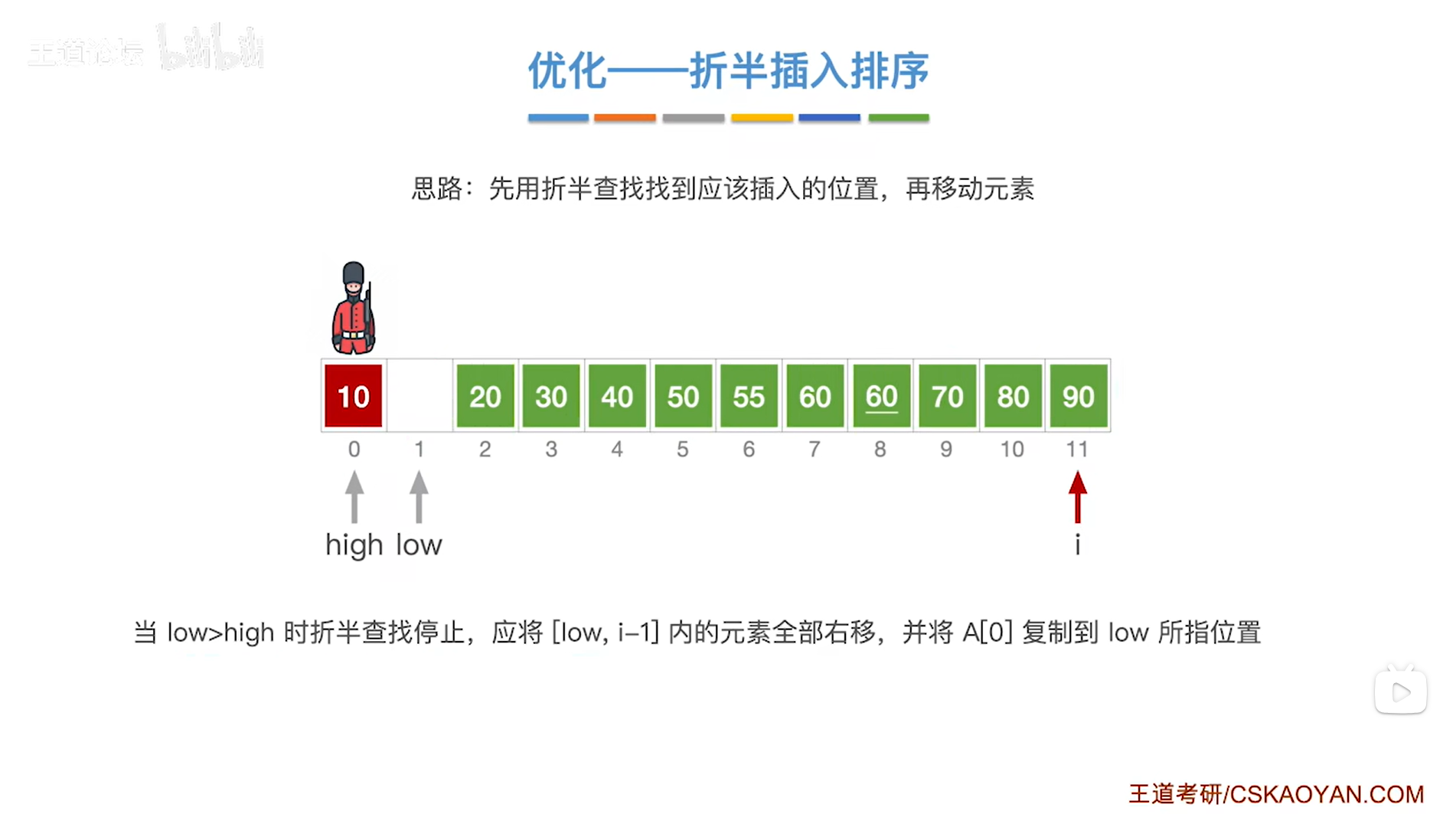
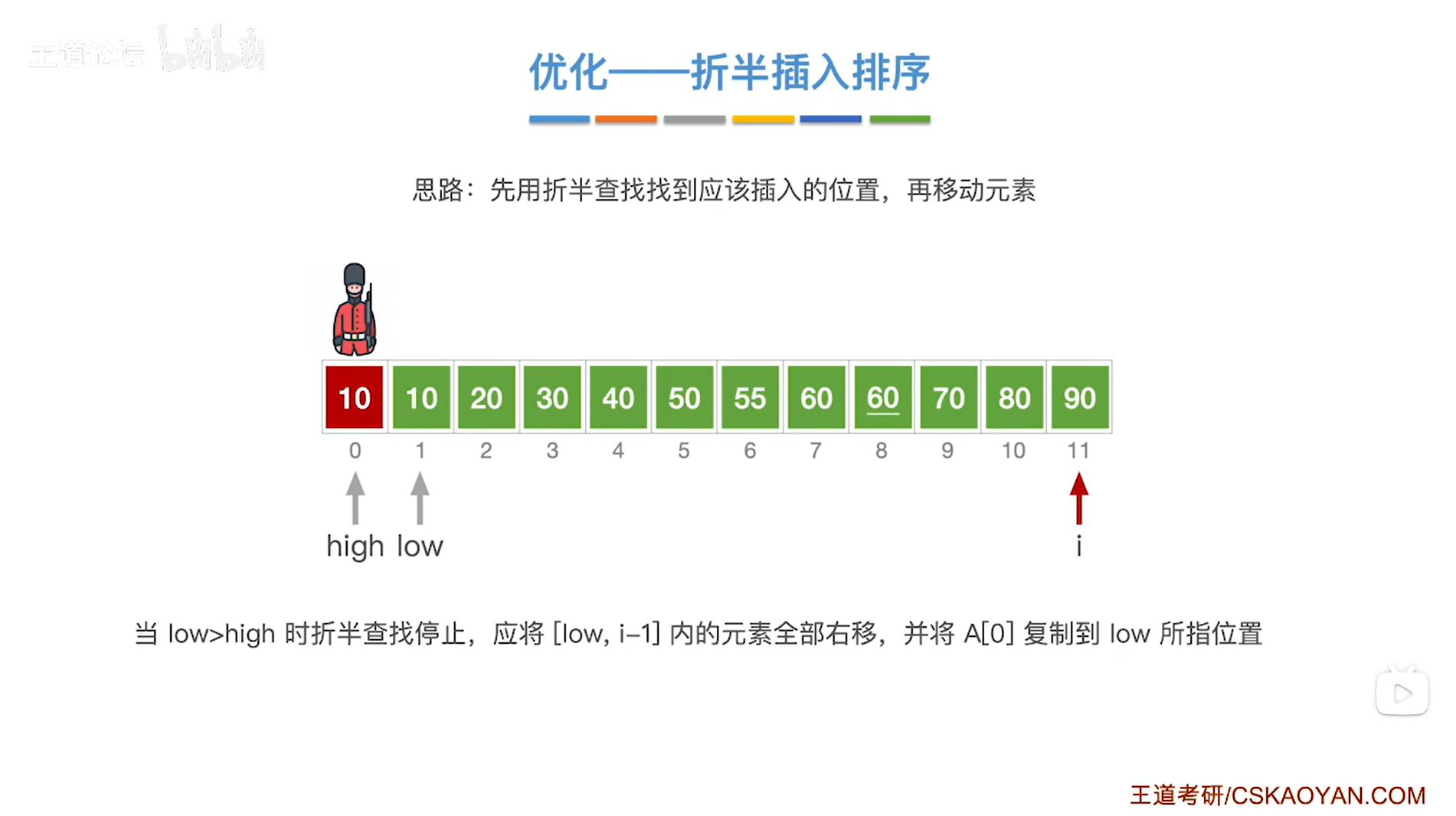
如上图，

总之，在插入排序中，确定当前处理的元素应该插入的位置的时候，由于该元素前面的序列已经是有序的状态，所以可以使用折半查找的方式来更快的确定应插入的位置，

折半查找最终都会因为low>high而停止，此时要做的就是把[low,i-1]区间内的元素全部右移一位，由于折半查找停止时最终high在low左边相邻一位的位置，所以low等于high+1，所以也可以写成把[high+1,i-1]区间内的元素全部右移一位，

另外，为了保证算法的稳定性，当找到和当前处理的元素的值相同的元素时，应继续在中间指针mid所指的位置右边的区间内继续寻找应插入的位置，

如下图：

3.代码实现：

#include<stdio.h>
​
//折半插入排序(带哨兵)->此时按照递增排序
void InsertSort(int A[],int n)
{
    int i,j;
    int low,high,mid;
    for(i=2;i<=n;i++) //依次将A[2]~A[n]插入前面的已经排好序的序列(为什么到A[n],main函数里的例子可以解释) 
    {
        A[0]=A[i]; //将A[i]暂存到A[0]
        low=1;high=i-1; //设置折半查找的范围
        while(low<=high) //折半查找(默认递增有序) 
        {
            mid=(low+high)/2; //取中间点
            if(A[mid]>A[0]) high=mid-1; //查找左半子表
            else low=mid+1; //查找右半子表(这里包括A[mid]<A[0]和A[mid]==A[0]，A[mid]==A[0]也是查找右半子表) 
        }
        for(j=i-1;j>=high+1;j--) 
        {
            A[j+1]=A[j]; //统一后移元素，空出插入位置 
        }
        A[high+1]=A[0]; //插入操作 
    }
} 
​
int main()
{
    int A[]={0,49,38,65,97,76,13,27,49}; //A数组的长度为9 
    InsertSort(A,8); //InsertSort第二个参数要传入8，因为A数组虽然长度为9，但0索引上的元素不参与排序即只有8个元素参与排序，刚好传入的8也是最后一个元素的索引，意味着排序的最后一个元素也在8索引上 
    for(int i=0;i<9;i++) //A数组的最后一个索引为8 
    {
        printf("%d \n",A[i]); //A数组的排序结果从1索引开始，0索引是哨兵即不用管 
    } 
    return 0;
}

---

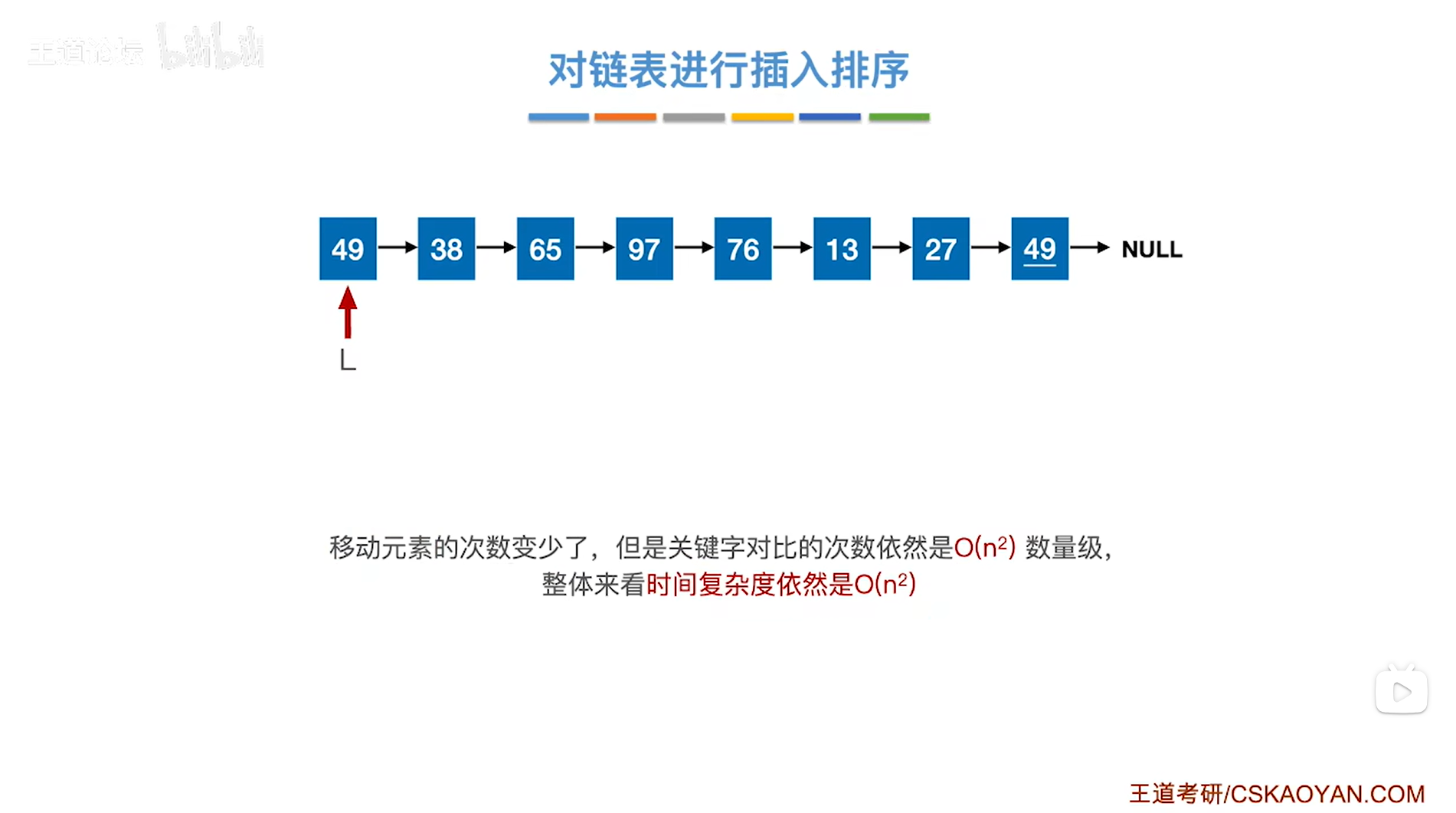
六.对链表进行插入排序：

• 对链表进行插入排序，具体的代码自行练习

1.参与插入排序的元素采用顺序存储和链式存储的区别：

如果参与插入排序的元素基于顺序存储，那么查找当前处理的元素应插入的位置既可以用顺序查找，也可以用折半查找；

如果参与插入排序的元素基于链式存储，那么查找当前处理的元素应插入的位置只可以用顺序查找，不可以用折半查找，因为链表不具备随机存储的特性即链表中的元素没有索引这个概念，就无法确定折半查找范围。

2.参与插入排序的元素采用链式存储的优点：

参与插入排序的元素采用链式存储相比于采用顺序存储的优点在于，参与排序的元素采用链式存储，当移动一个元素的时候，其实只需要修改几个指针即可，并不需要像顺序存储一样把很多元素依次右移，所以这种情况下移动元素的次数变少了。

3.参与插入排序的元素采用链式存储的时间复杂度：

假设共有n个元素需要插入排序，且参与插入排序的元素采用链式存储，

外层循环用于遍历处理每一个元素，内层循环在确定当前处理的元素应插入的位置时就只能顺序依次遍历比较各个关键字来确定当前处理的元素应插入的位置，

所以最终的时间复杂度依然会保持O(n²)的数量级，因此整体来看时间复杂度还是O(n²)。

---

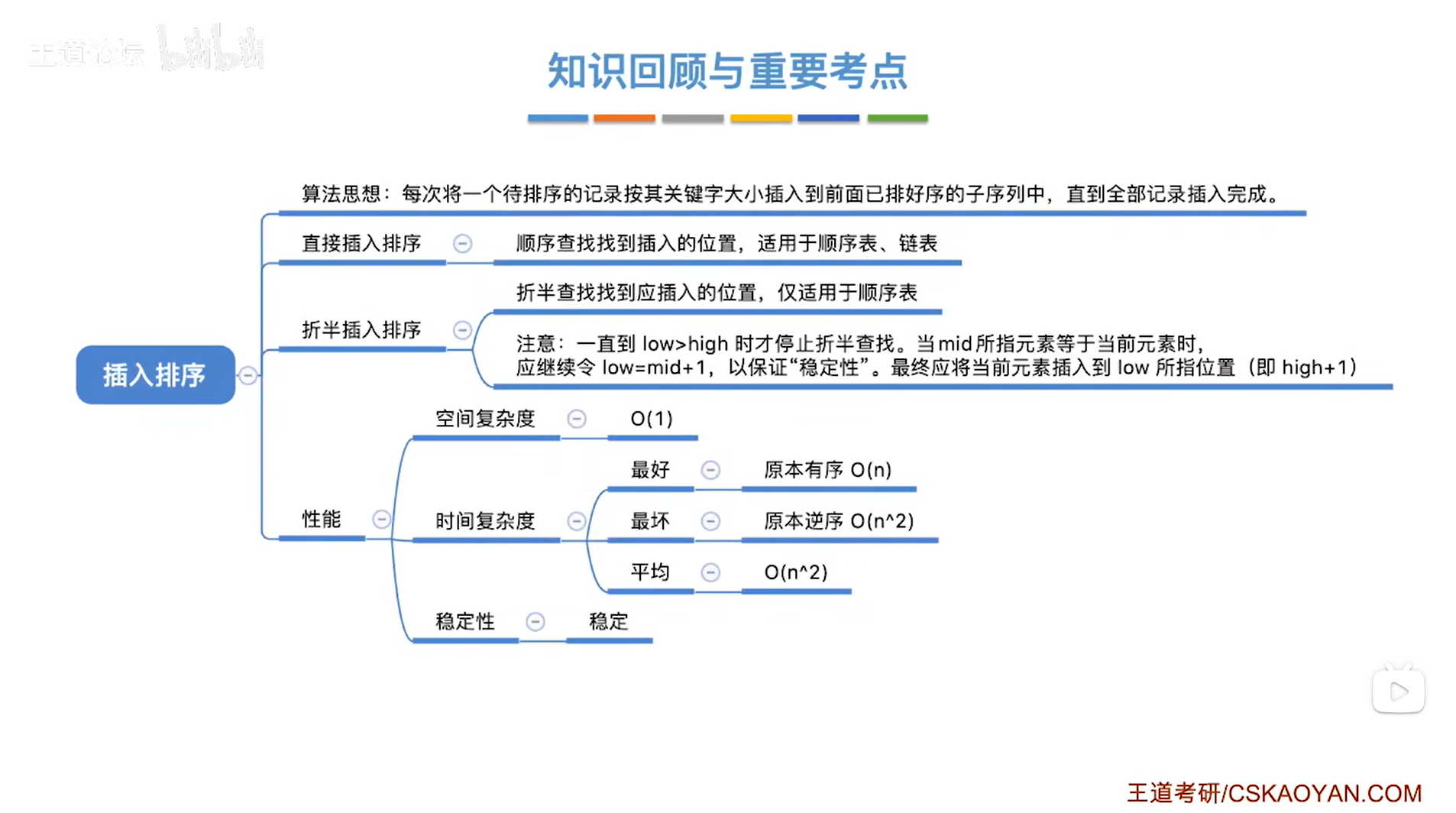
七.总结：

• 假设共有n个元素需要排序，只要采用插入排序，最终的时间复杂度都是O(n²)

• 注：如果给出的元素序列本来就是有序或者基本接近有序，这种情况下采用插入排序进行排序也可以得到一个很好的执行效果

---