括号配对（区间DP）_括号匹配情况数 dp-优快云博客

这篇博客主要讲解了一道与密码脱落题目相似但匹配规则不同的算法问题。该问题要求根据左右括号匹配规则，利用区间动态规划（DP）求解最长满足条件的子串长度。博主给出了详细的思路分析，包括转移状态的设定和代码实现，特别提到了第三个性质的处理。代码使用C++编写，展示了如何通过三层循环更新dp数组以找到最长匹配子串。

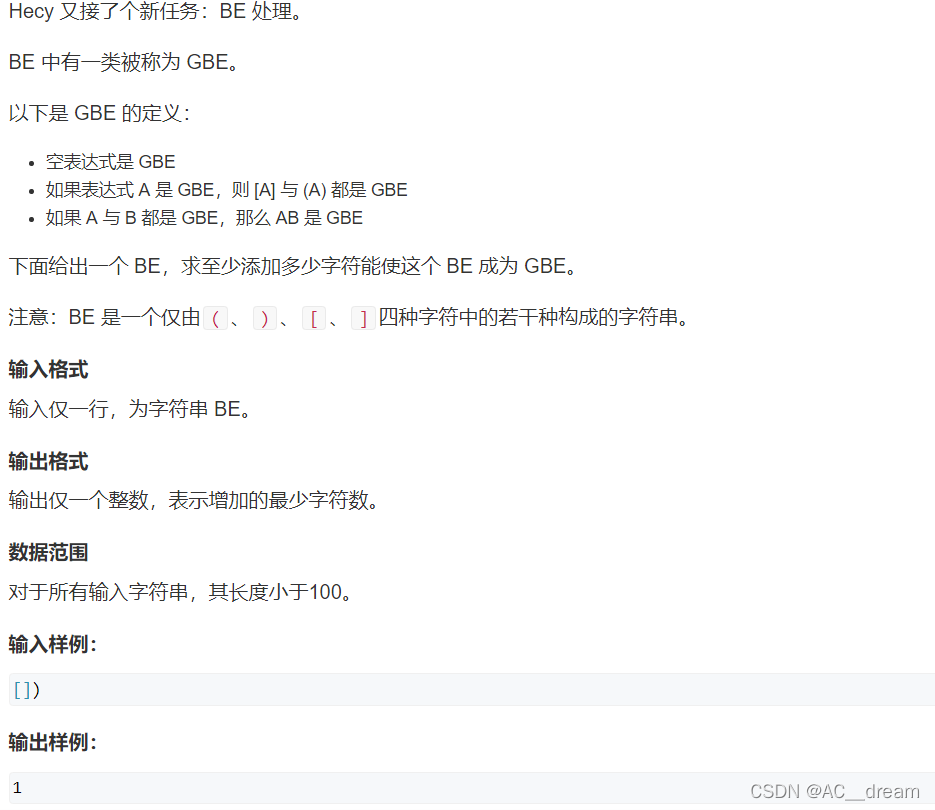
分析：这道题和我博客中密码脱落那道题非常相似，但是有一点不同的是，这道题的匹配规则是左右括号，而密码脱落那道题中匹配规则是相同字母，还有一点区别就是这道题中第三个条件需要特殊处理一下，这是密码脱落那道题目中所不具有的。区间DP的模板知识我在这就不细讲了，不了解的可以看下我之前博客，下面进行这道题思路的分析：

dp[i][j]表示字符串中第i个字符到第j个字符中满足GBE性质的最长字符串长度，答案依旧是字符串长度减去dp[1][l]，与密码脱落那道题目不同的是dp[i][j]有三个转移途径，第一个是dp[i+1][j],就是说第i个字符并不组成最长GBE，第二个是dp[i][j-1],就是说第j个字符不组成最长GBE，第三个途径是dp[i][k]+dp[k+1][j],这个转移途径是通过该题中第三个性质得到的，我们需要枚举一下k来对dp[i][j]进行一下更新，取这三个途径的最大值即可，建议不是很明白的同学先看下密码脱落那道题，比较具有启发意义

下面是代码：

#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
#include<map>
#include<cmath>
#include<queue>
using namespace std;
const int N=103;
int dp[N][N];
char s[N];
int main()
{
	scanf("%s",s+1);
	int l=strlen(s+1);
	for(int len=2;len<=l;len++)
	{
		for(int i=1;i+len-1<=l;i++)
		{
			int j=i+len-1;
			if((s[i]=='('&&s[j]==')')||(s[i]=='['&&s[j]==']'))
				dp[i][j]=dp[i+1][j-1]+2;
			else
				dp[i][j]=max(dp[i+1][j],dp[i][j-1]);
			for(int k=0;k<len;k++)
				dp[i][j]=max(dp[i][j],dp[i][i+k]+dp[i+k+1][j]);
		}
	}
	printf("%d",l-dp[1][l]);
	return 0;
}