Description
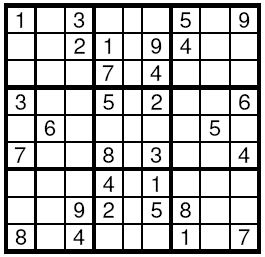
Input
Output
Sample Input
1 103000509 002109400 000704000 300502006 060000050 700803004 000401000 009205800 804000107
Sample Output
143628579 572139468 986754231 391542786 468917352 725863914 237481695 619275843 854396127
哦呵呵,这竟然是一道和实际应用有关的题,是不是做出了这道题然后所有的数独都是可以被破解的。=。= 醉了
就是一道dfs的题目,然后竟然正搜和反搜时间会差那么多,额 ,我不知道原因,在此也请高人请教。
首先,我的想法是:肯定是有三种状态的。
1.是在同一行的数字要不相同,所以我们对在同一行的进行一个数组的存储
2.是在同一列的数字要不相同,所以我们对在同一列的进行一个数组的存储
3.是在同一个3*3的格子里面的要不相同,那么这里我们也用一个数组来储存它们,这里一开始我卡住了,不知道要怎么才能存下来,后来也看了网上许多的题解,发现也有点难懂,于是就进行了直接裸的暴力,直接对每个格子for,然后存下来它们已经有的数字就好了。 暴力打法~sad。。。
*这里唯一要注意的就是在dfs中进行下标的输出的时候要小心,然后就是在dfs中进行分类讨论,首先是当前状态是0,没有被填充的时候,那么就对数字进行枚举,然后填进去;然后是被填充的时候,那么就跳过,进行下一个位置的枚举,注意当如果是当前行的最后一个的时候,那么要写成dfs(x+1,0),即为从下一行的第一个位置重新开始枚举。
#include<stdio.h>
#include<string.h>
#include<iostream>
#include<algorithm>
using namespace std;
#define maxn 11
char a[maxn][maxn];
int row[maxn][maxn],line[maxn][maxn],grid[maxn][maxn];
bool ff=false;
void dfs(int x,int y){
if(x==-1) {ff=true; return;}
if(a[x][y]!='0'){
if(y==0) dfs(x-1,8);
else dfs(x,y-1);
return ;
}
else if(a[x][y]=='0'){
for(int i=1;i<=9;i++){
if(!line[y][i]&&!row[x][i]&&!grid[x/3*3+y/3][i]){
a[x][y]=i+'0';
line[y][i]=1; row[x][i]=1; grid[x/3*3+y/3][i]=1;
if(y==0) dfs(x-1,8);
else dfs(x,y-1);
if(ff) return ;
line[y][i]=0; row[x][i]=0; grid[x/3*3+y/3][i]=0;
a[x][y]='0';
}
}
}
}
int main(){
int T;
scanf("%d",&T);
while(T--){
memset(row,0,sizeof(row)); memset(line,0,sizeof(line));
memset(grid,0,sizeof(grid));
for(int i=0;i<9;i++) scanf("%s",a[i]);
//以下是判断每一行中出现过的数字;
for(int i=0;i<9;i++){
for(int j=0;j<9;j++){
if(a[i][j]-'0'!=0) row[i][a[i][j]-'0']=1;
}
}
//以下是判断每一列中出现过的数字;
for(int j=0;j<9;j++){
for(int i=0;i<9;i++){
if(a[i][j]-'0'!=0) line[j][a[i][j]-'0']=1; //j代表是第几列;
}
}
//暴力求格子;
for(int i=0;i<3;i++)
for(int j=0;j<3;j++)
if(a[i][j]-'0'!=0) grid[0][a[i][j]-'0']=1;
for(int i=0;i<3;i++)
for(int j=3;j<6;j++)
if(a[i][j]-'0'!=0) grid[1][a[i][j]-'0']=1;
for(int i=0;i<3;i++)
for(int j=6;j<9;j++)
if(a[i][j]-'0'!=0) grid[2][a[i][j]-'0']=1;
for(int i=3;i<6;i++)
for(int j=0;j<3;j++)
if(a[i][j]-'0'!=0) grid[3][a[i][j]-'0']=1;
for(int i=3;i<6;i++)
for(int j=3;j<6;j++)
if(a[i][j]-'0'!=0) grid[4][a[i][j]-'0']=1;
for(int i=3;i<6;i++)
for(int j=6;j<9;j++)
if(a[i][j]-'0'!=0) grid[5][a[i][j]-'0']=1;
for(int i=6;i<9;i++)
for(int j=0;j<3;j++)
if(a[i][j]-'0'!=0) grid[6][a[i][j]-'0']=1;
for(int i=6;i<9;i++)
for(int j=3;j<6;j++)
if(a[i][j]-'0'!=0) grid[7][a[i][j]-'0']=1;
for(int i=6;i<9;i++)
for(int j=6;j<9;j++)
if(a[i][j]-'0'!=0) grid[8][a[i][j]-'0']=1;
ff=false;
dfs(8,8);
for(int i=0;i<9;i++){
printf("%s\n",a[i]);
}
}
}





 本文介绍了一种使用深度优先搜索解决数独问题的算法。通过记录行、列及3x3宫内已出现的数字,确保每一步填充都符合数独规则。采用递归方式填充空格,并在找到解决方案后停止搜索。
本文介绍了一种使用深度优先搜索解决数独问题的算法。通过记录行、列及3x3宫内已出现的数字,确保每一步填充都符合数独规则。采用递归方式填充空格,并在找到解决方案后停止搜索。
















 1784
1784

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








