参考链接
- 参考论文:
- 参考博客:
一、 梯度消失/梯度爆炸问题:
-
首先我们对如下的前向神经网络,我们讨论一下其BP算法:
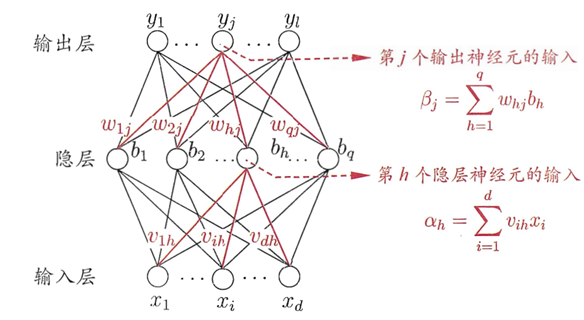
-
BP算法在求每层参数 w h j w_{hj} whj和 v i h v_{ih} vih的梯度前都是先求解每层神经元输入 β j β_j βj和 α h α_h αh的梯度,即: σ ε σ w h j = σ ε σ β j σ β j σ w h j = b h σ ε σ β j = b h δ j 2 \frac{σε}{σw_{hj}}=\frac{σε}{σβ_j}\frac{σβ_j}{σw_{hj}} =b_h \frac{σε}{σβ_j}=b_h δ_j^2 σwhjσε=σβjσεσwhjσβj=bhσβjσε=bhδj2 σ ε σ v i h = σ ε σ α h σ α h σ v i h = x i σ ε σ α h = x i δ h 1 \frac{σε}{σv_{ih}}=\frac{σε}{σα_h }\frac{σα_h}{σv_{ih}}=x_i \frac{σε}{σα_h}=x_i δ_h^1 σvihσε=σαhσεσvihσαh=xiσαhσε=xiδh1
-
其中 δ l δ^l δl表示第 l l l层神经元输入的梯度,也是该层的误差项。 δ l + 1 δ^{l+1} δl+1与 δ l δ^l δl是相关的,比如: σ ε σ α h = σ ε σ b h σ b h σ α h = ( ∑ j l σ ε σ β j σ β j σ b h ) f ′ ( α h ) \frac{σε}{σα_h}=\frac{σε}{σb_h}\frac{ σb_h}{σα_h}=(∑_j^l\frac{σε}{σβ_j} \frac{σβ_j}{σb_h })f'(α_h) σαhσε=σbhσεσαhσbh=(j∑lσβjσεσbhσβj)f′(αh) δ h 1 = ( ∑ j l w h j δ j 2 ) f ′ ( α h ) = ∑ j l ( f ′ ( α h ) ∗ w h j ) δ j 2 δ_h^1=(∑_j^l w_{hj} δ_j^2 )f'(α_h )=∑_j^l(f' (α_h )*w_{hj} )δ_j^2 δh1=(j∑lwhjδj2)f′(αh)=j∑l(f′(αh)∗whj)δj2其中 f f f为神经元激活函数。由上面表达式可以看出第2层的误差项 δ j 2 δ_j^2 δj2以比例 f ′ ( α h ) ∗ w h j f'(α_h )*w_{hj} f′(αh)∗whj传递到第1层的误差项 δ h 1 δ_h^1 δh1。
-
如果在很深的神经网络中, 如果每层传输比例 f ′ ( α h ) ∗ w h j f'(α_h )*w_{hj} f′(αh)∗whj都小于1,则较深的 L L L层的误差项 δ L δ^L δL传递到较底层时可能已经被放缩成了0,这就出现了梯度消失。如果每层传输比例 f ′ ( α h ) ∗ w h j f'(α_h )*w_{hj} f′(αh)∗whj都大于1,则较深的 L L L层的误差项 δ L δ^L δL传递到较底层时可能已经被放缩成了非常大的一个量,这就出现了梯度爆炸。
-
上面讨论的是特殊的前向神经网络,现在我们讨论一下一般的神经网络:
- 令第l层的净输入为 z ( l ) z^{(l)} z(l)输出为 a ( l ) a^{(l)} a(l),则一层神经外科可以表示为: z ( l ) = H ( a ( l − 1 ) ) a ( l ) = g ( z ( l ) ) z^{(l)}=H(a^{(l-1)}) \\a^{(l)}=g(z^{(l)}) z(l)=H(a(l−1))a(l)=g(z(l)) H ( ∗ ) H(*) H(∗)为该层的内部运算,依照网络类型有所不同,一般都是线性运算; g ( ∗ ) g(*) g(∗)是第l层的输出激活函数,是非线性运算.
- 第
l
l
l层的某参数更新需要计算损失
ϵ
ϵ
ϵ对其的梯度,该梯度依赖于该层的误差项:
δ
(
l
)
=
∂
ϵ
∂
z
(
l
)
δ^{(l)}=\frac{∂ϵ}{∂z^{(l)} }
δ(l)=∂z(l)∂ϵ 根据链式法则,
δ
(
l
)
δ^{(l)}
δ(l) 又依赖于后一层的误差项
δ
(
l
+
1
)
δ^{(l+1)}
δ(l+1) :
δ
(
l
)
=
∂
z
(
l
+
1
)
∂
z
(
l
)
δ
(
l
+
1
)
=
γ
(
l
)
δ
(
l
+
1
)
δ^{(l)}=\frac{∂z^{(l+1)}}{∂z^{(l)}} δ^{(l+1)}=γ^{(l)} δ^{(l+1)}
δ(l)=∂z(l)∂z(l+1)δ(l+1)=γ(l)δ(l+1)
γ
(
l
)
<
1
γ^{(l)}<1
γ(l)<1时,第
l
l
l层的误差项较后一层减小,如果很多层的情况都是如此,就会导致反向传播中,梯度逐渐消失,底层的参数不能有效更新,这也就是梯度消失。
当 γ ( l ) < 1 γ^{(l)}<1 γ(l)<1时,则会使得梯度以指数级速度增大,造成系统不稳定,也就是梯度爆炸问题。
-
梯度爆炸/消失问题可以通过Batch Normalization等技术避免
二、 网络退化问题:
-
网络退化问题:在神经网络可以收敛的前提下,随着网络层数的增加,训练集loss先逐渐下降,然后达到一个最小值,当到达该最小值后再继续增加网络深度的话,训练集loss反而会增大,注意这并不是过拟合,因为在过拟合中训练loss是一直减小的。这个现象被称为:退化(degradation)现象。如下图所示:
从上图可以看出在模型训练过程中,同样的训练轮次下,退化的网络也比稍浅层的网络的训练错误更高,所以可知网络退化问题不是过拟合导致的
-
网络退化情况下,相同结构的 K K K层网络 f K f_K fK会比 K + L K+L K+L层网络 f K + L f_{K+L} fK+L取得更优的结果,这与我们常理是不合:因为如果我们将 f K f_K fK的所有参数都复制到 f K + L f_{K+L} fK+L的前 K K K层,而将 f K + L f_{K+L} fK+L的后 L L L层学习为恒等映射。那么 f K + L f_{K+L} fK+L就可以取得和 f K f_K fK一样的效果。按照这个逻辑如果 K K K还不是所谓“最佳层数”,那么更深的网络就可以取得更好的结果。总而言之,与浅层网络相比,更深的网络的表现不应该更差。
-
所以一个合理的猜测就是,对神经网络来说,恒等映射并不容易拟合。即 f K + L f_{K+L} fK+L的后 L L L层很难学习到一个恒等映射,才会使得 f K f_K fK效果比 f K + L f_{K+L} fK+L效果好。为了解决这个问题我们可以在神经网络中直接引入直接映射,这就形成了残差网络。
三、 残差网络的形式:
-
既然神经网络不容易拟合一个恒等映射,那么一种思路就是直接向网络中加入恒等映射。假设神经网络每层的输入和输出维度一致,可以将神经网络每层要拟合的函数 H ( x ) H(x) H(x)拆分成两个部分,即: x l + 1 = H ( x l ) = x l + F ( x l ) x_{l+1}=H(x_l)=x_l+F(x_l) xl+1=H(xl)=xl+F(xl)其中x_l就是恒等映射,而 F ( x l ) = H ( x l ) − x l F(x_l)=H(x_l)-x_l F(xl)=H(xl)−xl为目标与输入的差,即残差,所有 F ( x l ) F(x_l) F(xl)叫残差函数。当 F ( x l ) → 0 F(x_l)→0 F(xl)→0时该层就学习到了一个恒等映射。
-
残差快图:
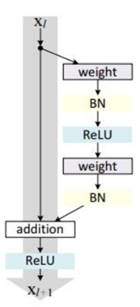
-
残差块分成两部分:直接映射部分和残差部分
- 直接映射:对应上图的左边的直线。用 h ( x l ) h(x_l) h(xl)
- 残差部分: 对应上图的右边的部分,一般由两个或者三个卷积操作和Batch_Normalization构成,用 F ( x l , W l ) F(x_l,W_l) F(xl,Wl)表示。
- 图中的Weight是指卷积操作
- addition是指单位加操作
- BN是Batch_Normalization
-
为了使得两条路径的输出能进行addition需要统一Feature Map的数量,所以在直接映射中加一个1×1卷积进行升维或者降维.所以最终表达式为: x l + 1 = f ( h ( x l ) + F ( x l , W l ) ) x_{l+1}=f(h(x_l )+F(x_l,W_l )) xl+1=f(h(xl)+F(xl,Wl))
-
残差网络很好地解决了深度神经网络的退化问题,并在ImageNet和CIFAR-10等图像任务上取得了非常好的结果,同等层数的前提下残差网络也收敛得更快。这使得前馈神经网络可以采用更深的设计。除此之外,去除个别神经网络层,可以应用到各中网络中去。
四、 残差网络的原理:
-
残差块一个更通用的表示方式是: x l + 1 = f ( h ( x l ) + F ( x l , W l ) ) x_{l+1}=f(h(x_l )+F(x_l,W_l )) xl+1=f(h(xl)+F(xl,Wl))
-
两个假设:
- h ( x l ) h(x_l ) h(xl)是直接映射,即先不考虑升维或者降维的情况
- f ( ) f() f()也是直接映射,上图表示的 f f f为ReLU。
-
那么这时候残差块可以表示为: x l + 1 = x l + F ( x l , W l ) x_{l+1}=x_l+F(x_l,W_l ) xl+1=xl+F(xl,Wl)
-
现在从 l l l使用上式一直递推到更深的 L L L层可以得到: x L = x l + ∑ i = l L − 1 F ( x i , W i ) x_L=x_l+∑_{i=l}^{L-1}F(x_i,W_i ) xL=xl+i=l∑L−1F(xi,Wi)由此可知 L L L层可以表示为任意一个比它浅的 l l l层和他们之间的残差部分之和
-
可以从第0成开始地推: x L = x 0 + ∑ i = 0 L − 1 F ( x i , W i ) x_L=x_0+∑_{i=0}^{L-1}F(x_i,W_i ) xL=x0+i=0∑L−1F(xi,Wi) L L L层可以表示为各个残差块特征的累加。
-
损失函数 ϵ ϵ ϵ关于 x l x_l xl的梯度可以表示为: ∂ ϵ ∂ x l = ∂ ϵ ∂ x L ∂ x L ∂ x l = ∂ ϵ ∂ x L ( 1 + ( ∂ ∑ i = 0 L − 1 F ( x i , W i ) ∂ x l ) = ∂ ϵ ∂ x L + ∂ ϵ ∂ x L ∂ ∑ i = 0 L − 1 F ( x i , W i ) ∂ x l \frac{∂ϵ}{∂x_l}=\frac{∂ϵ}{∂x_L} \frac{∂x_L}{∂x_l}=\frac{∂ϵ}{∂x_L} (1+(∂∑_{i=0}^{L-1} \frac{F(x_i,W_i ) }{∂x_l })\\=\frac{∂ϵ}{∂x_L}+\frac{∂ϵ}{∂x_L} \frac{∂∑_{i=0}^{L-1}F(x_i,W_i ) }{∂x_l} ∂xl∂ϵ=∂xL∂ϵ∂xl∂xL=∂xL∂ϵ(1+(∂i=0∑L−1∂xlF(xi,Wi))=∂xL∂ϵ+∂xL∂ϵ∂xl∂∑i=0L−1F(xi,Wi)
-
在整个训练过程中 ∂ ∑ i = 0 L − 1 F ( x i , W i ) ∂ x l \frac{∂∑_{i=0}^{L-1}F(x_i,W_i ) }{∂x_l} ∂xl∂∑i=0L−1F(xi,Wi)不可能一直为-1,这样 ∂ ϵ ∂ x l \frac{∂ϵ}{∂x_l} ∂xl∂ϵ不可能一直为0,也就是说不会出现梯度消失的问题
-
∂ ϵ ∂ x l \frac{∂ϵ}{∂x_l} ∂xl∂ϵ表示 L L L层的梯度可以直接传递到任何一个比它浅的 l l l层
-
通过上面分析分析,我们发现,当残差块满足上面两个假设时,信息可以非常畅通的在高层和低层之间相互传导,说明这两个假设是让残差网络可以训练深度模型的充分条件。
-
现在说明直接映射是最好的选择:
- 我们采用反证法,假设 h ( x l ) = λ l x l h(x_l )=λ_l x_l h(xl)=λlxl,则残差块的表示的为: x l + 1 = λ l x l + F ( x l , W l ) x_{l+1}=λ_l x_l+F(x_l,W_l ) xl+1=λlxl+F(xl,Wl)
- 对于更深的 L L L层: x L = ( ∏ i = l L − 1 λ i ) x l + ∑ i = l L − 1 ( ( ∏ i = l + 1 L − 1 λ i ) F ( x i , W i ) ) x_L=(∏_{i=l}^{L-1} λ_i )x_l+∑_{i=l}^{L-1}((∏_{i=l+1}^{L-1}λ_i )F(x_i,W_i )) xL=(i=l∏L−1λi)xl+i=l∑L−1((i=l+1∏L−1λi)F(xi,Wi))
- 对于
∏
i
=
l
L
−
1
λ
i
∏_{i=l}^{L-1}λ_i
∏i=lL−1λi 部分有:
- 当 λ > 1 λ>1 λ>1 时,很有可能发生梯度爆炸
- 当 λ < 1 λ<1 λ<1 时,很有可能发生梯度消失
- 所以 λ λ λ必须等1
- 对于其它不影响梯度的
h
(
∗
)
h(*)
h(∗),例如LSTM中的门机制(下图c和d)、Dropout(下图f)以及用于降维的1×1卷积(下图e)试验效果图如下:
试验的结果为:
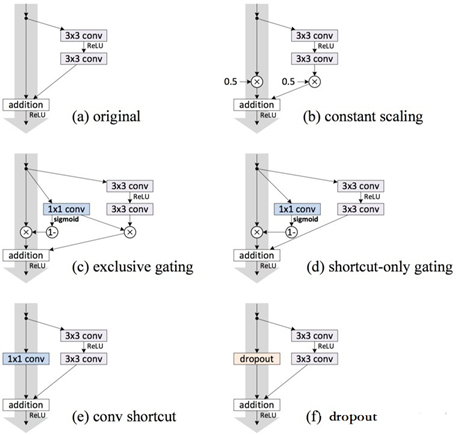 在所有的变异模型中,依旧是直接映射的效果最好
在所有的变异模型中,依旧是直接映射的效果最好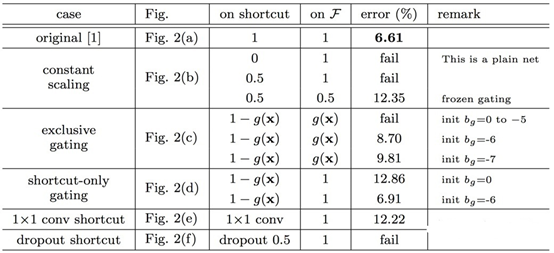
- Exclusive Gating:在LSTM的门机制中,绝大多数门的值为0或者1,几乎很难落到0.5附近。当g(x)→0时,残差块变成只有直接映射组成,阻碍卷积部分特征的传播;当g(x)→1时,直接映射失效,退化为普通的卷积网络;
- Short-cut only gating:g(x)→0时,此时网络便是直接映射的残差网络;g(x)→0 时,退化为普通卷积网络;
- Dropout:类似于将直接映射乘以1-p,所以会影响梯度的反向传播;
- 1×1 conv:1×1卷积比直接映射拥有更强的表示能力,但是实验效果却不如直接映射,说明该问题更可能是优化问题而非模型容量问题。
-
激活函数的位置试验
- 试验图:
试验结果:
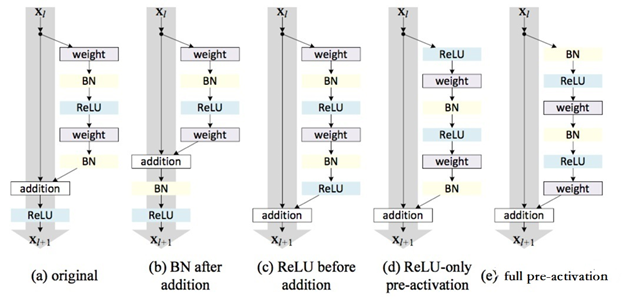 实验结果也表明将激活函数移动到残差部分可以提高模型的精度
实验结果也表明将激活函数移动到残差部分可以提高模型的精度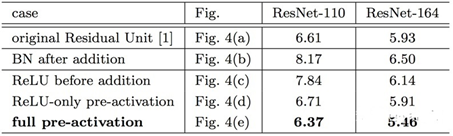
- 试验图:





 本文深入探讨了深度神经网络中的梯度消失与爆炸问题,解释了网络退化现象,并介绍了残差网络如何解决这些问题。通过引入恒等映射,残差网络能够有效缓解梯度消失与爆炸,同时克服网络退化,实现深层网络的良好训练。
本文深入探讨了深度神经网络中的梯度消失与爆炸问题,解释了网络退化现象,并介绍了残差网络如何解决这些问题。通过引入恒等映射,残差网络能够有效缓解梯度消失与爆炸,同时克服网络退化,实现深层网络的良好训练。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








