轨迹生成概述

原创于 2026-01-03 15:35:45 发布 · 276 阅读

CC 4.0 BY-SA版权

在2024年6月时，写了一些关于6轴机械臂相关的学习笔记。如今已是2026年初，时间过得嗖嗖滴~由于是机械臂相关的从业者，所学习的知识大抵都与机械臂相关。继续学习《机器人学导论》的其他部分，开始第七章——轨迹的生成。

1、概述

轨迹描述了机械臂在多维空间中期望的运动。轨迹：指的是每个自由度的位置、速度和加速度的时间历程。用户只需给定末端执行器的期望的目标位姿，而由系统来确定到达目标的准确路径、时间历程、速度曲线等。

此外，规划好的轨迹如何在计算机中描述也是一个值得关注的问题。最后，要研究通过内部表达式计算轨迹的问题——即轨迹生成问题。大多数情况下，在轨迹生成的运行时间内需要计算位置、速度和加速度。这些轨迹由计算机计算，因此要以某种速率来计算轨迹点，此速率叫路径更新率。在典型的机械臂系统中，路径更新率在60Hz到2000Hz之间。

2、关于路径描述和轨迹生成的综述

在大多数情况下，将操作臂的运动看作是工具坐标系｛T｝相对于工作台坐标系｛S｝的运动。这两种运动的方式是相同的，因为用户会感到按照这种方式描述路径和生成路径是非常有利的。

当按照工具坐标系相对于工作台坐标系的运动来指定路径时，其实是将运动的描述与任何具体的机器人、末端执行器或工件相分离。由此得到的模型，可将相同的路径描述应用于不同的操作臂或者用于具有不同工具尺寸的相同操作臂上。进而，总是可以通过相对于工作台坐标系的运动规划来确定和规划运动着的工作台（可能是一个传送带）的运动，而且在轨迹生成的运行时间内使得｛S｝的定义随时间变化。

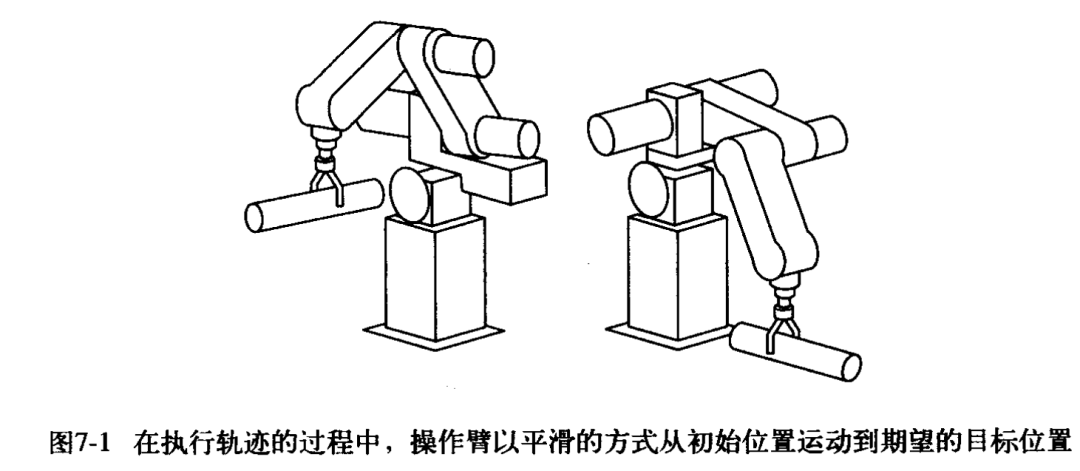
如图7-1所示，一个基本问题是将操作臂从初始位置移动到某个最终期望位置——也就是将工具坐标系从当前值{Tinit}移动到最终期望值｛Tfinal｝。要注意，一般而言，运动包括工具相对于工作台的姿态变化和位置变化。

有时需要指定运动的更多细节而不只是简单地指定最终的期望位形。一种方法是在路径描述中给出一系列的期望中间点（位于初始位置和最终期望位置之间的过渡点）。因此，为了完成这个运动，工具坐标系必须经过中间点所描述的一系列过渡位置与姿态。每个中间点实际上都是确定工具相对于工作台的位置与姿态的坐标系。路径点这个术语包括了所有的中间点以及初始点和最终点。需要记住的是，虽然通常使用“点”这个术语，但实际上它们是表达位置和姿态的坐标系。除了运动中的这些空间约束之外，用户可能还希望指定运动的瞬时属性。例如，在路径描述中可能还需要指定各中间点之间的时间间隔。

通常，期望机械臂的运动是平滑的。为此，要定义一个连续的且具有连续一阶导数的光滑函数。有时还希望二阶导数也是连续的。一般而言，急速的运动会加剧机构的磨损，激起机械臂共振。因此，为了保证路径平滑，必须在各中间点之间，对路径的空间和时间特性给出一些限制条件。

这样看存在着多种选择，因此可以使用很多方法来制定和规划路径。任何通过中间点的光滑函数都可以用来制定精确的路径。本章将从中选取一些简单的函数进行讨论。

欢迎关注：

其他机械臂相关笔记：