【机器学习】损失函数（代价函数）、目标函数 | 经验风险、期望风险、结构风险

损失函数（代价函数）

0-1损失函数：
$$L(Y,f(x))=\{\begin{array}{ll}1,& \text{if Y = f(x)}\\ 0,& \text{if Y != f(x)}\end{array}$$
平方损失函数：$L(Y,f(x))=(Y-f(x){)}^2$
绝地值损失函数：$L(Y,f(x))=|Y-f(x)|$
对数损失函数：$L(Y,p(Y|X))=-logp(Y|X)$
损失函数我们只能知道模型决策函数$f(X)$对于单个样本点的预测能力

经验风险

如果想知道模型$f(X)$对训练样本中所有的样本的预测能力应该怎么办呢？显然只需所有的样本点都求一次损失函数然后进行累加就好了。如下式
$Ob{j}_1=\frac{1}{N}{\sum }_{i=1}^{N}L(y_i,f(x_i))$
经验风险越小说明模型$f(X)$对训练集的拟合程度越好，但是对于未知的样本效果怎么样呢？
怎么来衡量这个模型对所有的样本（包含未知的样本和已知的训练样本）预测能力呢？熟悉概率论的很容易就想到了用期望。

期望风险（理想，不实用）

插个题外话，EM算法(Expection Max 期望最大化)，也是一直在逼近最大期望

对于连续\离散函数，$期望=\sum 值\ast 概率$,即下式：
$Ob{j}_2=E[L(Y,f(x))]={\int }_{x\ast y}L(Y,f(x))\ast P(x,Y)\mathrm{d}x\mathrm{d}y$
这就是期望风险，期望风险表示的是全局的概念，表示的是决策函数对所有的样本$(X,Y)$预测能力的大小.
而经验风险则是局部的概念.理想的模型（决策）函数应该是让所有的样本的损失函数最小的（也即期望风险最小化）。
现在我们已经清楚了期望风险是全局的，理想情况下应该是让期望风险最小化，但是呢，但是期望风险函数往往是不可得到的，即上式中，X与Y的联合分布函数不容易得到。怎么办呢？那就用局部最优的代替全局最优这个思想吧。这就是经验风险最小化的理论基础。

通过上面的分析可以知道，经验风险与期望风险之间的联系与区别。现在在总结一下：

1、经验风险是局部的，基于训练集所有样本点损失函数最小化的；期望风险是全局的，是基于所有样本点的损失函数最小化的。
2、经验风险函数是现实的，可求的；期望风险函数是理想化的，不可求的。

只考虑经验风险的话，会出现过拟合的现象，怎么办呢？这个时候就引出了结构风险。

结构风险（目标函数）

结构风险是对经验风险和期望风险的折中。
在经验风险函数后面加一个正则化项（惩罚项）便是结构风险了。如下式：
$Ob{j}_3=\frac{1}{N}{\sum }_{i=1}^{N}L(y_i,f(x_i))+\lambda J(f(x))$
结构风险 = 目标函数 = 经验风险 + 正则项/惩罚
如此，加上惩罚项，图三的目标函数也就没有那么小了。

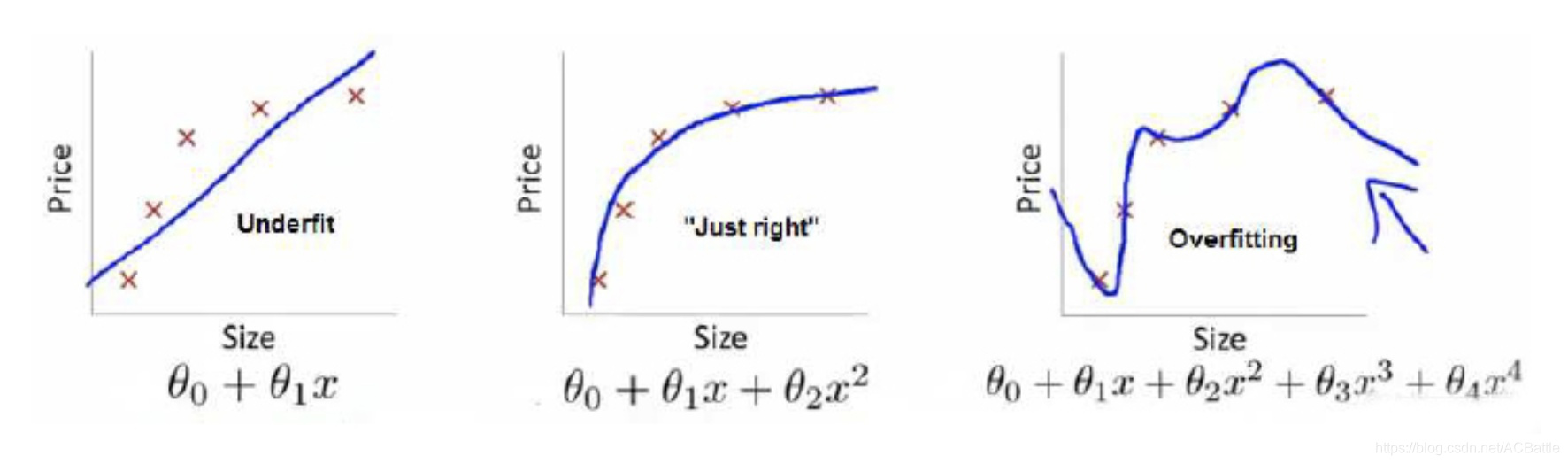
借用吴恩达老师视频的例子，图三的损失函数最小（预测与真实值的误差），经验风险最小（过拟合），正则化最大，结构风险最大（拟合函数出现4次方，比较复杂）。

参考知乎@zzanswer的回答、机器学习–>期望风险、经验风险与结构风险之间的关系