第4章 神经网络的学习
4.1 从数据中学习
4.1.1 数据驱动
先从图像中提取
特征量
,
再用机器学习技术学习这些特征量的模式。
在计算机视觉领域,常用的特征量包括SIFT、
SURF
和
HOG
等。使用这些特征量将图像数据为向量,然后对转换后的向量使用机器学习中的SVM
、
KNN
等分类器进行学习。
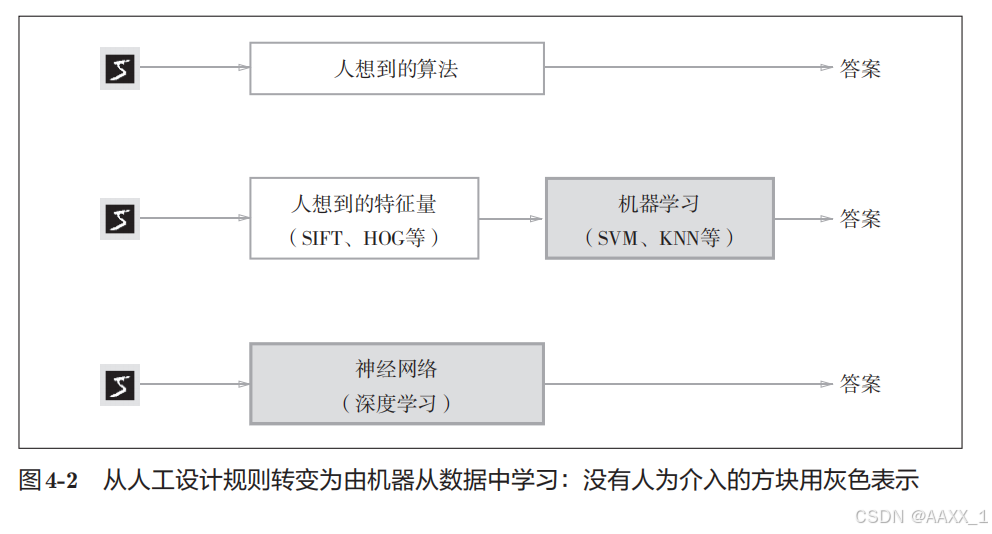
深 度 学 习 有 时 也 称 为 端 到 端 机 器 学 习(end-to-end machinelearning)。这里所端到端 是指从一端到另一端的意思,也就是从原始数据(输入)中获得目标结果(输出)的意思。
4.1.2 训练数据和测试数据
机器学习中,一般将数据分为
训练数据
和
测试数据
两部分来进行学习和实验等。
为了正确评价模型的
泛化能力,就必须划分训练数据和测试数据。
训练数据也可以称为
监督数据。
4.2 损失函数
损失函数是表示神经网络性能的“恶劣程度”的指标,即当前的神经网络对监督数据在多大程度上不拟合,在多大程度上不一致。
损失函数可以使用任意函数,但一般用均方误差和交叉熵误差等。
如果给损失函数乘上一个负值,就可以解释为“在多大程度上不坏”,即“性能有多好”。
4.2.1 均方误差
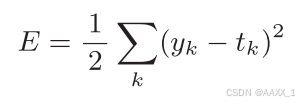
y
k
是表示神经网络的输出,
t
k
表示监督数据,
k
表示数据的维数。
def mean_squared_error(y, t):
return 0.5 * np.sum((y-t)**2)>>> # 设“2”为正确解
>>> t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
>>>
>>> # 例1:“2”的概率最高的情况(0.6)
>>> y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
>>> mean_squared_error(np.array(y), np.array(t))
0.097500000000000031
>>>
>>> # 例2:“7”的概率最高的情况(0.6)
>>> y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
>>> mean_squared_error(np.array(y), np.array(t))
0.597500000000000034.2.2 交叉熵误差
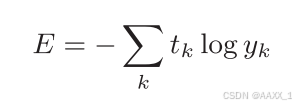
log
表示以
e
为底数的自然对数(
log
e
)。
y
k
是神经网络的输出,
t
k
是正确解标签。
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))>>> t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
>>> y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
>>> cross_entropy_error(np.array(y), np.array(t))
0.51082545709933802
>>>
>>> y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
>>> cross_entropy_error(np.array(y), np.array(t))
2.30258409299454584.2.3 mini-batch学习
计算损失函数时必须将所有的训练数据作为对象。也就是说,如果训练数据有100
个的话,我们就要把这
100
个损失函数的总和作为学习的指标。
以交叉熵误差为例:
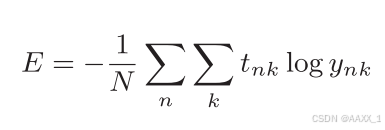
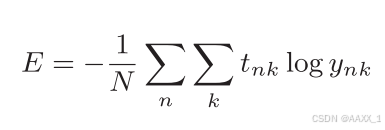
神经网络的学习也是从训练数据中选出一批数据(称为
mini-batch
,
小批量),然后对





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1445
1445

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








