3D空间的几种变换方式

欧式变换

欧式变换是最简单的3D变换方式，由旋转和平移组成。它保持了向量的长度和夹角，相当于我们把一个刚体原封不动的进行了移动或旋转，不改变它自身的样子。其矩阵表现形式如下所示：

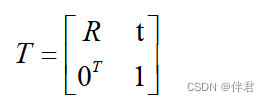
其中，旋转矩阵R为行列式为1的正交矩阵。t为平移矩阵。

相似变换

相似变换比欧式变换多了一个自由度，它允许物体进行均匀缩放，其矩阵表示为：

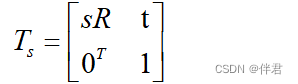
注意，旋转部分多了一个缩放因子s,表示我们在对向量旋转之后，可以在x,y,z三个坐标上进行均匀缩放。由于含有缩放，相似变换不再保持图形的面积不变。

仿射变换

仿射变换的矩阵形式如下：

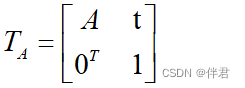
与欧式变换不同的是，仿射变换只要求A是一个可逆矩阵，而不必是正交矩阵。放射变换也叫正交投影。经过仿射变换之后，立方体就不再是方的了，但是各个面仍然是平行四边形。

射影变换

射影变换是最一般的变换，它的矩阵形式为：

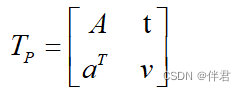
它的左上角为可逆矩阵A，右上角为平移矩阵t，左下角为缩放a^T。由于采用了齐次坐标，当v≠0时，我们可以对整个矩阵除以v得到一个右下角为1的矩阵；否则得到右下角为0的矩阵。因此，2D的射影变换一共有8个自由度，3D则有15个自由度。从真实世界到相机照片的变换可以看成一个射影变换。

总结

变换名称	自由度	不变性质
欧式变换	6	长度、夹角、体积
相似变换	7	体积比
仿射变换	12	平行性、体积比
射影变换	15	接触平面的相交和相切