随机电路的精度与能量权衡

在随机电路设计中以精度换取能量

47

阿明·阿拉吉，华盛顿大学陈韦廷，加州大学圣地亚哥分校约翰·P·海耶斯， 密歇根大学安德鲁·B·康 和 李佳佳，加州大学圣地亚哥分校

随着我们接近传统摩尔定律缩放的极限，能够更高效地消耗能量的替代计算技术变得更具吸引力。随机计算（ SC）作为一种重新兴起的计算技术，是图像处理和通信等若干重要应用中传统二进制电路的一种低成本且容错的 替代方案。SC允许自然的精度‐能量权衡，这一特性在过去已被加以利用。本文提出了一种用于SC电路的精度‐能 量权衡技术，在几乎不损失精度的情况下降低了其能耗。为此，我们采用电压或频率缩放，这通常会以时序错误 为代价来降低能耗。然后我们证明，由于SC电路固有的容错性，即使在激进的缩放下，它们仍能令人满意地运行 而不会造成显著的精度损失。这显著提高了它们的能效。相比之下，当电源电压降低时，传统二进制电路会迅速 失效。为了找到SC电路的能效最优工作点，我们提出了一种误差估计方法，使我们能够快速探索电路的设计空间。 该误差估计方法基于马尔可夫链和最小二乘回归。此外，我们研究了在如此激进的缩放下优化SC电路的机会。我 们发现，逻辑与物理设计技术可以结合使用，以显著扩展SC本身已十分强大的精度‐能量权衡可能性。特别是，我 们证明了在电压和频率缩放下，对路径延迟的仔细调整可导致显著的误差降低。我们通过缓冲器插入和绕线实现 更加平衡的路径延迟。这些技术不同于传统的路径平衡技术，后者的目标是通过调整非关键路径的尺寸来最小化 功耗。我们的路径平衡方法的目标是提高在电压/频率缩放的SC电路中的错误抵消机会。我们的电路优化综合考虑 了因插入的缓冲器和导线带来的功耗开销与因更平衡的路径延迟所实现的供电电压降标所带来的能耗降低之间的 权衡。仿真结果表明，我们的优化后的随机计算电路可以承受激进的电压缩放，而不会出现显著的信噪比(SNR) 下降。在一个例子中，对SC电路进行40%供电电压降低（从1V降至0.6V）实现了66%节能（从20.7pJ降至 6.9pJ），并使其比相应的传统二进制电路更高效。在同一示例中，优化电路的100%频率提升（时钟周期从 400ps缩短至200ps）未引起显著的SNR下降。我们还表明，工艺偏差和温度变化对优化后的SC电路影响有限。 当温度变化100◦C或工艺条件从最坏情况变为最佳情况时，误差变化小于5%。

本文是Alaghi等人[2015]的扩展和修订版本。本工作得到了国家科学基金会资助号CCF‐1318091以及IMPACT+ 中心、三星公司、高通公司和恩智浦公司的支持。作者地址：A. Alaghi，华盛顿大学计算机科学与工程系， 185史蒂文斯大道，西雅图，华盛顿州，98195‐2350；电子邮件：armin@cs.washington.edu；W.‐T. J. 陈和 李杰，加州大学圣地亚哥分校电气与计算机工程系，9500吉尔曼大道#0407，拉霍亚，加利福尼亚州， 92093‐0407；电子邮件：{wechan, jil150}@ucsd.edu；J. P. 海耶斯，密界大学电气工程与计算机科学系， 2260海沃德街，安娜堡，密歇根州，48109‐2121；电子邮件：jhayes@eecs.umich.edu；A. B. 卡恩，加州大 学圣地亚哥分校计算机科学与工程系，9500吉尔曼大道#0404，拉霍亚，加利福尼亚州，92093‐0404；电子邮件： abk@cs.ucsd.edu。允许为个人或课堂教学目的制作本作品的部分或全部数字或纸质副本，但前提是不得出于盈 利或商业利益而制作或分发这些副本，并且在每份副本的首页或显示界面的初始屏幕中必须注明此声明及完整引 用信息。对于本作品中由非美国计算机协会（ACM）拥有的组成部分，其版权必须予以尊重。允许带署名的摘要 使用。如需其他方式复制、重新发布、上传至服务器、再分发至列表，或在其他作品中使用本作品的任何组成部 分，则需事先获得特定许可和/或支付费用。可向美国计算机协会（ACM）出版部申请许可：2宾夕法尼亚广场 701室，纽约，纽约州10121‐0701，美国，传真+1(212) 869‐0481，或发送邮件至permissions@acm.org。 c© 2017美国计算机协会 1550‐4832/2017/04‐ART47 15.00美元 DOI: http://dx.doi.org/10.1145/2990503

美国计算机协会 期刊 计算系统新兴技术期刊，第13卷第3期，文章47，出版日期：4月 017.

47:2 A. Alaghi 等人

CCS概念： Hardware→物理设计（电子设计自动化）； 容错； 工艺、电压和温度变化； 新兴架构； 附加关键词和短语：随机计算，能耗降低，误差建模

美国计算机协会参考格式： 阿明·阿拉吉，魏廷 J . 陈，约翰·P·海耶斯，安德鲁·B·康，和李佳佳。2016年。在随机电路设计中以精度换取能量。《计算机系统 新兴技术杂志》13, 3, 文章47 (2017年4月), 30页。数字对象标识符: http://dx.doi.org/10.1145/2990503

1. 引言

随着传统摩尔定律扩展接近极限，能量和功耗限制给集成电路（IC）设计人员带来了重大 挑战。许多嵌入式系统，如可穿戴设备和医疗植入物，由于电池容量和生理限制，对功耗 和能量有严格要求[Lee et al. 2013]。例如，设计不良的可植入电路中过高的功耗可能会 损坏人体组织[Chun et al. 2014]。为应对这些能量/功耗问题，已提出多种方法。值得注 意的是，嵌入式系统通常针对特定应用进行设计；这使得设计人员可以使用专用硬件，其 物理和/或逻辑特性优于传统设计。

随机计算（SC）[Gaines 1969；Poppelbaum 等人 1967]已被提出作为一种替代的 低功耗计算技术，适用于多种重要的嵌入式处理应用。随机计算电路通过简单逻辑门对 （伪）随机比特流执行复杂计算。图1展示了一个实现函数 Z = 1 4+ 1 条位流所表示的数值是其出现 1 的概率。例如，出现在 x1,、x2, 和 z 处的随机数（SNs） X1,、X2, 和 Z 分别表示 9 12, 8 12, 6 12,。该电路有两个主输入 x1 和 x2,，以及两个辅助输入 r1 和 r2。辅助输入是值为 1/2 的恒定随机数。图1中的与非门实现了随机函数 Y1= 1−X1 X2,，该函数涉及乘法和减法。或门实现了 Y2=R1+R2−R1R2,，由于 R1=R2= 1 2，因此 得到 Y2= 3 4。最后，异或门实现了函数 Z = Y1+ Y2 −2Y1Y2= 1 4+ 1 SC的主要优势，如图1所示，是使用简单逻辑门实现复杂的算术功能。例如，单个与 门即可实现乘法。与传统二进制乘法器相比，随机计算乘法器的尺寸小几个数量级。然而， 这以牺牲速度为代价。SC电路需要在随着精度增加而呈指数增长的位流上运行，因此完成 一次计算所需的时间要长得多。这一直是SC的主要缺点。运行时间的指数级损失不仅影响 性能，而且在使用长位流时还会导致过高的能耗[Moons 和 Verhelst 2014]。因此，随 机计算电路主要适用于低精度计算[Aguiar 和 Khatri 2015]。一些近期的工作致力于通 过使用确定性数源来减少SC电路的运行时间[Alaghi 和 Hayes 2014]，或通过消除时 钟分配树的功耗开销来解决这一问题[Najafi et al. 2016]。

本文利用随机计算的容错性，通过电压/频率缩放来降低随机计算电路的能耗。SC电路 具有容错性，因为单个比特上的错误对长比特流的数值影响极小，且多个错误倾向于相互 抵消。最后，SC电路提供了一种自然的能效‐精度权衡：比特流长度N，即时钟周期数，即 SC电路执行一次计算所使用的时钟周期数，直接影响其能耗和精度。

美国计算机协会 期刊 计算系统新兴技术期刊，第13卷第3期，文章47，出版日期：4月20日 17.

在随机电路设计中以精度换取能量 47:3

随机计算（SC）在1960年代首次提出时，因其允许简单实现算术函数而具有吸引力。 然而，在随后的几十年中，由于晶体管成本降低，性能成为主要设计目标，传统二进制计 算占据了主导地位。尽管如此，在那些年代中，SC在某些应用中仍然有用，包括人工神经 网络的高效实现[Kim 和 Shanblatt 1995；Brown 和 Card 2001；Canals 等人2016]。 世纪之交之后，由于随机计算（SC）在低功耗嵌入式处理应用中的潜力，其重新受到关注。 一些近期成功的应用包括低密度奇偶校验（LDPC）解码 [Gaudet 和 Rapley 2003；Lee 等， 2015；Gross 等 2005]以及图像处理 [Li 和 Lilja 2011；Alaghi 等，2013；Fick 等2014]。其 他近期的随机计算应用还包括数据识别与挖掘 [Chippa 等，2014；Morro 等 2015],、机器 学习 [Gupta 和 Gopalakrishnan 2014],以及动力系统 [王 等 2015]。需要注意的是，Lee 等 [2015]和 Fick 等[2014]所提出的经硅验证的随机计算设计，其性能优于相应的传统二进制 设计。

如前所述，我们研究了将电压缩放等低功耗技术应用于随机计算（SC），旨在获得超 低能耗需求的电路。电压缩放即降低电路的电源电压，可减少电路的能耗，但会增加其延 迟。如果应用允许一定的延迟开销，则可以在偶尔产生错误输出的代价下采用激进的电压 缩放。因此，电压缩放使设计者能够以精度换取能量。该方法在非随机计算文献中已得到 广泛研究[He 等，2012；Hegde 和 Shanbhag 2001；Kahng 等 2010],，并已提出容忍 和/或纠正时序错误的方法。然而，随着电压缩放的加剧，时序违规的概率迅速增加，因而 需要复杂的纠错方法。

在本文中，我们表明具有代表性的SC电路可以容忍高达40%电压降低而不会产生显著 误差。图2展示了一个示例电路，并直观地说明了为何我们可以激进地调节SC电路的电压/ 频率。其思想在于，我们可以在前一组输入信号完全通过电路传播之前施加新的输入信号。 在理想场景下（如图2(c)所示），所有输入信号以相同的速度通过不同层级传播；该场景 与波流水线[Burleson等 1998]的概念非常相似。

本工作的主要贡献是一种优化方法，可在电压/频率缩放下改善随机计算电路的精度‐ 能量权衡。该方法基于图2的观察结果。为了实现图2(c)所示的理想场景，我们需要修改电 路以确保信号同时传播。为此，我们采用综合和物理设计技术，在保持电路功能不变的同时，有效挽回任何损失的精度。

美国计算机协会 期刊 计算系统新兴技术期刊，第13卷第3期，文章47，出版日期：4月20日 17.

47:4 A. Alaghi 等人

在综合步骤中，我们采用自然平衡的电路结构。请注意，这与电路的逻辑级平衡不同， 因为我们关注的是随机等效的电路[Chen 和 Hayes 2015],，这意味着即使它们实现的底 层逻辑函数可能不同，但实现的随机函数相同。现有的逻辑级工具无法理解此类等效性。

理想情况下，传统的布局布线（P&R）流程会尽可能平衡路径延迟（例如，利用非关 键路径的时序裕量来降低功耗和面积）。然而，由于设计约束（例如最大转换或最大电容） 以及门尺寸受限，路径延迟通常无法完全平衡，尤其是当各路径深度差异较大时。图3展示 了我们提出的优化方法。假设门G1已缩小至最小尺寸并采用高Vth（阈值电压），但由于 路径深度不同，从x{1 ,2,3,4}到z的延迟与从x{5 ,6}到z的延迟仍未完全平衡。我们的研究表明 （见第4节），这种不平衡的路径延迟会增加经电压/频率缩放的SC电路的计算误差。为了 提高随机电路的精度，我们提出通过缓冲器插入和导线绕行进一步平衡路径延迟。如图 3(b)所示，我们在路径中插入缓冲器（以红色显示）

美国计算机协会 期刊 计算系统新兴技术期刊，第13卷第3期，文章47，出版日期：4月20日 17.

在随机电路设计中以精度换取能量 47:5

非关键路径。尽管插入的缓冲器会带来功率惩罚，但它们能够实现更多的频率和/或电压缩 放，从而在给定精度要求下降低电路的延迟和能耗。据我们所知，这是首次在随机计算 （SC）背景下采用此类技术。此外，为了指导设计空间探索，我们在第3.3节中展示了基 于Alaghi等人[2015]模型的改进型计算误差马尔可夫链模型。通过应用最小二乘回归，我 们提高了Alaghi等人[2015]中的建模精度。

需要注意的是，“随机计算”这一术语最近也被用于描述涉及概率行为的传统电路， 包括电压/频率缩放的场景[Sartori 等人 2011；Shanbhag 等人 2010]。我们所指的SC是 一种在1960年代提出的计算技术[Gaines 1969；Poppelbaum 等人 1967]，与Sartori等 人[2011]和Shanbhag等人[2010]中使用的概念无关。

本文中，我们仅关注组合型SC电路。Qian和Riedel [2008]以及钱等人[2011]展示了 组合型SC电路与伯恩斯坦多项式[Lorentz 1986]之间的联系，并证明了SC组合电路仅能 实现某些类型的多项式函数。在本文中，我们采用可重构随机计算（ReSC）[钱等人 2011]作为实现大多数测试用例的主要方法。正如我们将在后文讨论的那样，竞争性设计 方法[Alaghi和Hayes 2015]不如ReSC能效高。

我们注意到，文献中也存在实现更广泛函数类的时序SC电路 [Li 和 Lilja 2011； Saraf 等人 2013；Brown 和 Card 2001]。Brown 和 Card [2001]是最早在神经网络背 景下发展时序SC电路理论的研究者之一。特别是，他们通过使用一个简单的有限状态机来 实现Sigmoid函数。然而，本文不涉及时序电路的相关内容，将其留作未来工作。本文使 用的Sigmoid测试用例是一种组合实现，与Brown和Card [2001]设计的电路无关。我们 还注意到，组合电路可以通过利用相关性 [Alaghi 和 Hayes 2013]来实现非多项式函数， 并且我们的优化方法能够处理这类函数。

本文的结构如下。第2节简要回顾了随机计算（SC），以及在电压/频率缩放条件下的 误差分析。同时阐述了随机数生成对随机电路精度的影响。第3节提出了两个

美国计算机协会 期刊 计算系统新兴技术期刊，第13卷第3期，文章47，出版日期：4月20日 17.

47:6 A. Alaghi 等人

随机‐t o‐二进制转换器)

相关的优化问题，以及一种为期望的精度等级寻找SC电路最小能量工作点的直接方法。还 讨论了一种用于SC电路的快速误差估计方法。第4节探讨了在不同电压等级下优化SC电路 的机会。第5节给出了实验结果，最后，结论部分在第6节中给出。

2.随机计算中的容错性与数生成

随机电路C是一种对（伪）随机比特流进行操作的逻辑电路，这种比特流称为随机数（ SNs）。xi是C中的一条导线，携带一个随机数Xi。Xi所传递的信息——在不会引起混淆的 情况下也可简便地用Xi表示——是其1脉冲的速率或频率，且与比特流长度无关。形式上， 长度为N、包含N1 1个1和N − N1 0个0的比特流被称为具有值或幅值Xi= N1/N的随机数。 这通常被解释为在比特流中随机选择一个位置时看到1的概率[Gaines 1969]。随机数的取 值范围在单位区间[0, 1],内，其精度由N决定。

图4展示了几个基本的SC组件。如前所述，单个与门（如图4(a)所示）实现SC乘法。 图4(b)显示了一个实现SC加法的多路复用器。由于随机数位于单位区间内，两个随机数的 和会落入区间[0, 2]，无法由随机数表示。为缓解此问题，通常应用1/2的缩放因子，使结 果回到单位区间内。因此，图4(b)中的电路实现了缩放加法 Z=(X+ Y)/2。

当与传统二进制电路一起使用时，随机计算电路的输入和输出必须经过转换过程。图 4(c)展示了一种二进制到随机数转换器，通常称为随机数生成器（SNG）。在每个时钟周 期，SNG将其k位二进制输入与一个均匀分布的随机数进行比较。结果，比较器输出为1的 概率与其二进制输入成正比。一些研究表明，图4(c)中的随机数生成器有时可以被简单计 数器[Alaghi 和 Hayes 2014]所替代。正如我们将在本节后面所示，随机数生成器的选择 会影响SC电路的功耗和精度。将随机数（SN）转换回二进制形式可以通过统计1的个数来 实现，因此图4(d)所示的二进制计数器足以完成此任务。

2.1. 误差分析

随机计算电路的固有容错性源于以下事实：当长度为N的随机数序列中发生单个位翻转时， 其幅值仅改变 1/N，而当N足够大时，这种变化是微不足道的。例如，图1所示电路输出 端的随机数序列，其中N= 12，表示Z= 6 12 。如果由于错误导致比特流中的某一位1或0发 生了变化，则有错误随机数序列为Z∗=Z ± 1 12 ，仅为最小变化。此外，由于随机数序列的 幅值由1的个数决定，而非其位置，因此若多个错误发生在相反方向，它们倾向于相互抵消[ Chen et al. 2013; Qian 2011; 钱等人 2011]。随机计算电路的概率特性，

美国计算机协会 期刊 计算系统新兴技术期刊，第13卷第3期，文章47，出版日期：4月20日 17.

在随机电路设计中以精度换取能量 47:7

再加上抵消可能性，使得评估随机计算电路的精度变得困难。

尽管本文将讨论时序错误的影响，但值得一提的是位翻转类型的错误如何影响随机数 （SN）。存在比特翻转的情况下，随机数的均方误差（MSE）可通过以下公式[Chen et al. 2013]计算。假设Z为无错误随机数序列，Z∗为有错误随机数序列，我们得到 MSE= E[(Z−Z∗)2]= p2 e ·(1−2·Z)2+ 1 N ·(Z·(1−Z)+pe·(1−pe)·(1−4·Z·(1−Z))),(1) 其中 E[∗]表示期望值（平均）算子，pe是随机数每位发生位翻转的概率，N是随机数序列长度。

公式(1)反映了错误抵消的影响：当Z= 1/2时，对于较大的N，误差变为零。然而，当Z = 1/2 时，抵消作用不大。在极端情况下，当Z= 0（或Z= 1）时，由于没有发生抵消，误差达到最 大。

本研究探讨了电压和频率缩放在SC电路中的应用。电压缩放指的是系统性地降低电源 电压（即“欠压”），这是一种用于降低数字电路功耗的标准技术。然而，这种缩放往往 会导致时序违规，从而可能引起输出错误。过于激进的电压缩放会在传统二进制电路中引 发大量时序错误，导致计算正确性的退化可能是灾难性的。而频率缩放是指以高于其标称 速度的时钟频率对电路进行时钟操作，代价是产生时序错误。可以使用诸如Razor [ Ernst et al. 2003]之类的设计方法，使传统电路更能抵抗由频率缩放引起的时序错误。 然而，这些技术仅在错误率相对较低时才有效。相比之下，当电压缩放或频率缩放极为激 进且时序错误率相对较高时，SC电路有可能实现计算正确性的优雅退化。此外，我们还可 以通过采用本文提出的设计方法来恢复损失的精度。

影响SC电路的错误类型与应用电压（或频率）缩放时的比特翻转有显著不同。通常情况下， 随机计算电路能够容忍位翻转类型的误差，因此可以预期它们也能容忍由缩放引起的时序错误。 正如我们接下来将展示的，随机计算电路在容忍此类时序错误方面表现得更好。

当0到1的跳变发生延迟时，可能会在SN Z中产生时序错误，此时1无法被及时捕获， 导致Z的幅值减少 1/N，其中N为比特流长度。类似地，在1到0跳变时，由于时序错误可 能导致0未被捕获，从而使Z的幅值增加 1/N。由于对于任意比特流而言，0到1和1到0的跳 变次数几乎相同（差异最多为一次），这些时序错误倾向于相互抵消。图5显示了一个受跳 变错误影响的SN示例。在此图中，Z有三个0到1和三个1到0的跳变，用箭头表示。由于延 迟错误，在错误情况下的Z∗遗漏了一些跳变，但最终结果的数目

美国计算机协会 期刊 计算系统新兴技术期刊，第13卷第3期，文章47，出版日期：4月20日 17.

47:8 A. Alaghi 等人

由于错误抵消，该值保持不变。在最近的一项工作中，Najafi 等人[2016]指出，随机计算电路 能够容忍由不同步时钟引起的时序变化。他们的观察结果与我们工作的结果一致。类似地， Perez‐Andrade 等人[2013]已证明，当存在由时钟缩放引起的定时错误时，SC LDPC译码器 仍能令人满意地运行。

现在，我们用e0→1和e1→0分别表示0到1和1到0的错误率。我们希望分析它们对随机数 Z的影响。我们假设在某个时钟周期发生转换错误的事件是从伯努利随机变量中独立采样的 样本，其参数为e0→1或e1→0，具体取决于转换方向。这一简化假设并非精确模型，毕竟底 层电路是确定性的。然而，在经电压/频率缩放的SC电路中存在多种现象会导致看似随机的 行为。首先，由于大多数情况下使用（伪）随机比特流，因此两个连续时钟周期内的信号 在统计上是独立的。这意味着输入信号并不总是激活相同的电路路径；被激活的路径取决 于前一时钟周期的信号，而这些信号是伪随机的。其次，SC电路的输出通常由计数器的触 发器采集，由于时序违规，输出触发器可能进入亚稳态并产生看似随机的结果。第三，当 电源电压降低时，电路更容易受到具有随机性质的环境噪声影响。本文未考虑这些现象各 自的直接影响，而是通过伯努利随机变量来建模它们的综合影响。需要注意的是，如果使 用确定性比特流（如我们的EdgeDetection测试用例），则伯努利随机变量的简化假设将 无法正确建模电路行为。

为简化起见，我们还假设Z的0到1和1到0转换次数相等。这些次数取决于两个因素： Z的值及其“活动性”。如果Z= 0或Z= 1，则转换次数将为零。当使用（伪）随机数源 生成Z时，通常在Z= 1/2时出现最多的转换次数。但是，正如我们将在下一小节中展示 的那样，随机数源的选择会影响转换次数。我们将活动因子A定义为介于0和1之间的数值， 具有以下特性：当A= 1时，在Z中的转换次数达到最大；而当其为0时，转换次数降至最 小。在Z= 1/2的情况下，最大转换次数为N，其中N是SN的长度。这对应于每个时钟周 期都发生转换的SN，例如，01010101010....Z= 1/2且A= 0的SN对应于具有最少转换 次数的比特流，例如，00000001111…。

我们现在可以计算跳变错误的影响。根据Chen等人[2013],的分析，我们发现跳变错 误会通过两种方式导致输出错误：它们会改变Z∗的平均值和方差。对于长度为N、活动因 子为A的无误差数Z，我们有 E[Z ∗ ]= 1 N · E[Z · N −N0→1 · e0→1+ N1→0 · e1→0], 其中ei→j表示 到 转换上的错误率，Ni→j表示通过计算得到的 到 转换次 数 N0→1= N1→0= 2 · Z ·(1 − Z)· A · N. 因此 E[Z ∗ ]= Z+ 2 · Z ·(1 − Z)· E[e1→0 −e0→1])· A. (2) 方程(2)有两个重要含义。首先，更重要的是，如果e0→1=e1→0，则Z和Z∗在平均情况 下将相等。其次，活动因子A也对误差有直接影响。我们将在下一节讨论活动因子的影响

美国计算机协会 期刊 计算系统新兴技术期刊，第13卷第3期，文章47，出版日期：4月20日 17.

在随机电路设计中以精度换取能量 47:9

小节。目前，让我们假设e0→1= e1→0= e是正确的。尽管Z∗的期望值与无误差的Z相同， 但由于e0→1和e1→0的概率特性，我们仍可能观察到随机波动。再次强调，如果仅使用确定 性信号，则不会出现随机波动。我们采用类似于Chen等人[2013],的方法计算均方误差， 即 MSE= E[(Z − Z∗)2]= 1 N2 · E[(Z · N −(Z · N −N ∗ 0→1+ N ∗ 1→0))2], 其中N ∗ i→j 是一个随机变量，表示 i 到 j 的跳变错误数量。现在我们有 MSE= 1 N2 · E[(N ∗ 0→1 −N ∗ 1→0)2]= 1 N2 ·(E[(N ∗ 0→1)2]+ E[(N ∗ 1→0)2] −2E[N ∗ 0→1 · N ∗ 1→0]). 由于N ∗ 0→1是参数为N0→1和e的二项随机变量，我们可以通过求N ∗ 0→1的二阶矩来计算上述方 程的第一项。 E[(N ∗ 0→1)2]= e2 · N0→1 ·(N0→1 −1)+ e · N0→1 并且，由于 E[(位流长度∗ 0→1) 2]= E[(位流长度∗ 1→0) 2],，我们得到 MSE= 1 N ·(4 · A · Z ·(1 − Z)· e ·(1 −e)). (3) 公式(3) 具有若干重要且违反直觉的含义： —由于电压缩放导致的误差可以通过增加位流长度N来减小。众所周知，增加N可以减少 随机计算中的随机波动误差[Gaines 1969],；Chen 等人观察到，当存在比特翻转时，增 加N并不会带来帮助[Chen et al. 2013]。 —活动因子 A也可能起到重要作用，因为降低 A 可减小均方误差。 —如果转换错误率e= 1/2，则误差达到最大。显然，如果我们设e= 0，可将误差降至零； 但 somewhat surprisingly，若将错误率增加至e= 1，我们同样得到MSE= 0。在这 种情况下，Z的每一次转换都存在错误，但由于转换次数相等，错误相互抵消。注意当e = 1时，电路中未见任何随机波动，电路行为是确定性地。此场景类似于图2(c)所示的期 望行为。

在上述三种影响中，增加N是最不理想的，因为它会增加电路运行时间，从而增加其 能耗。活动因子可以通过在输入端生成合适的随机数来控制（参见第2.2节）。平衡跳变错 误e0→1和e1→0是本文的主要目标，这将在接下来的章节中进行讨论。

我们强调，方程(2)和(3)基于若干简化假设，仅反映了延迟错误对单个信号Z的影响。 实际上，由于电路复杂性，这些假设可能不成立。例如，基于方程(2)的假设 e0→1= e1→0 能够带来理想的误差减少，但在现实世界示例中难以实现。我们将方程(2)作为希望趋近的 指导原则或理想情况。类似地，公式(3)为误差减少设定了指导原则，其中一些也难以实现。 例如，在我们的实验中从未观察到最终误差变为零的 e= 1 情况。此外，A= 0 是另一个 无法实现且使最终误差降为零的情况。然而，正如我们接下来将展示的，减小 A 可以降低 最终误差。

美国计算机协会 期刊 计算系统新兴技术期刊，第13卷第3期，文章47，出版日期：4月20日 17.

47:10 A. Alaghi 等人

2.2. 随机数生成

随机数生成是随机计算的一个重要步骤，直接影响精度和面积成本等参数。在随机计算文 献中对此已有相当广泛的研究[Jeavons 等人，1994；钱等人 2009]。尽管早期大多数关 于随机计算的工作假设随机数必须是（伪）随机的，但最近的一些研究表明，确定性随机 数也可以成功应用于随机计算[Fick 等人，2014；Alaghi 和 Hayes 2014]。

公式(3)表明，随机数的活动因子A直接影响其误差。有趣的是，活动因子还会影响动 态功耗[Pedram 1994],，因此降低A可同时降低功耗和误差。虽然在通用SC电路中无法 完全固定A，但通过谨慎选择随机数生成器，可以在一定程度上控制它。图6显示了三个表 示1/2且具有不同活动因子的随机数。最常用的随机数生成方法是使用（伪）随机数生成器[ Jeavons et al. 19

在随机电路设计中以精度换取能量

3. 问题描述与提出的解决方案

本节定义了本文所解决的两个主要问题，并讨论了一种误差估计方法，该方法可实现对电 压/频率缩放下的SC电路进行快速评估。

3.1. 寻找最小能量点

首先，我们提出并回答以下问题：“给定一个SC电路，在满足特定精度要求（errgoal）的 情况下，计算所需的最低能量是多少？” 为了量化电路的精度，可以采用多种错误度量方 法，例如最大误差、均方误差等。从现在开始，我们使用“平均误差”作为度量指标。 err= E[|Z − Z∗|], 其中Z是电路输出的正确值或“理想”值，Z∗是错误输出。Z与Z∗之间的差值在所有可能 输入上取平均。该平均误差指标将用于衡量SC电路和传统二进制电路的精度。需要注意的 是，我们选择平均误差作为精度指标是因为其简单性。我们下文提出的一般性方法并不局 限于特定的误差指标。然而，由于随机计算电路的概率特性，所有推导出的误差界限都将 是概率性的。

用于随机计算的随机数（SNs）的长度N控制着电路的精度以及总能耗。因此，通过 减小N，可以在精度与能量或功耗节省之间进行权衡。这种自然的权衡在过去已被成功应 用[Alaghi 等人 2013]。本文的研究表明，电压/频率缩放为SC电路的精度‐功耗权衡提供 了新的可能性。实际上，SC电路具有三个控制参数——(i) 电源电压Vdd，(ii) 时钟频率f， 以及(iii) 比特流长度N （或等效的时钟周期数），这些参数共同决定了其精度以及能量/功 耗。因此，寻找电路的最佳工作点成为一个新的且具有挑战性的问题。

以往的方法会搜索满足平均误差小于给定值errgoal的最小N。然而，如前所述，可以 同时调整三个参数（电源电压Vdd、时钟频率f和随机数长度N），以寻找最优解。我们将 三元组(Vdd, f,N)称为SC电路的一个工作点 。现在我们将上述问题形式化为以下问题描述。

最小能耗工作点问题 。给定一个SC电路，寻找满足平均误差精度要求 ≤errgoal的条件下， 具有最小能耗的工作点（Vdd, f,N）。1

除了在下一小节中为MEOP问题提供解决方案外，我们还考虑了优化以改善在电压缩 放条件下的误差行为。过度降低电源电压和/或提高工作频率可能导致信号在输出端z处的 实际到达时间（AAT）相对于时钟采样相位发生错位。不失一般性，对于SC电路中从输入 xi和xj到输出z的任意一对时序路径，我们假设它们在z处对应的到达时间分别为AATi和 AATj，使得ki ·T ≤AATi ≤(ki+1)·T 且 kj · T ≤AATj ≤(kj+ 1) · T，其中T为时钟周期。若ki ≠ kj，则称这两条时序路径 存在到达时间错位。换句话说，这两个信号无法在同一个时钟周期内被捕获。我们将说明 到达时间错位对随机计算电路的计算精度具有显著影响。图8展示了两条时序路径（弧x1 − z、x2 −z）的一个示例，用以说明到达时间对齐的重要性。在该示例中，情况(a)假设两条 路径均无时序违规，此情况生成正确的输出序列1, 0, 1。情况(b)中，两条时序路径均有时 序违规，但两个到达时间被捕捉于同一时钟周期内（即T2），因此不存在到达时间错位。 尽管两个信号均延迟了一个周期，但在z处的输出序列仍然正确，即为1, 0, 1。2在情况(c) 中，由于路径延迟不平衡，来自x1和x2的信号在两个不同的周期到达z。因此，情况(c)存 在导致计算误差的到达时间错位，如图8中的红色虚线椭圆所示。此外，通过调整采样相位 也无法恢复输出序列。

受上述讨论的启发，我们提出采用逻辑与物理设计技术来对齐SC电路输出端的到达时间。 如方程(2)所示，理想情况下0到1和1到0转换上的错误率应相等（e0→1和e1→0），因为平衡误 差可降低平均误差。因此，我们定义了以下问题描述，其解决方案将在第4节中讨论。

随机计算电路优化（SCOpt）问题 。 给定一个随机函数和一组电源电压范围，寻找一种在 给定电源电压范围内具有最小平均误差的电路实现。

3.2. MEOP问题的解决方案

我们现在提出针对上一节定义的MEOP问题的解决方案。简而言之，给定一个SC电路，我 们希望为给定的精度指标找到最能效最优工作点（Vdd，f，N）。我们解决该问题的方法 是在工作点空间内进行直接搜索。换句话说，我们尝试不同的工作点，并对每一个工作点 评估相应电路的精度和能量。

然后我们选择满足精度要求且能量最低的点。 与传统二进制电路不同，随机计算电路中的误差 tends to 相互抵消。此外，随机计算 电路具有非确定性特性，即其行为可以用概率来描述。由于这些原因，评估随机电路的精 度是not trivial。穷举仿真可用于评估小型随机电路的精度。然而，对于较大的电路，对 每个工作点进行穷举仿真是不切实际的。鉴于此，我们提出了一种快速误差估计方法。我 们注意到，我们的搜索策略并非新颖，但我们提出了一种新模型，能够实现对解空间的快 速探索。

3.3. 使用马尔可夫链进行误差估计

我们提出了一种马尔科夫链（MC）模型 [Grinstead 和 Snell 2003]来估计误差。该模型 假设涉及时序错误的SC电路可能处于正确或错误状态。在正确状态下，电路产生的输出 与没有时序错误的电路相同。由于存在两种可能的输出值，因此我们有两种正确状态：C 0,表示输出为0的状态，以及C1,表示输出为1的状态（图9）。除了正确状态外，还有四种 错误状态。在错误状态下，SC电路由于发生时序违规而产生错误结果。时序违规有两种形 式：(i) 延迟错误，即在输出端遗漏了0到1或1到0的转换；(ii) 毛刺，即输出本不应发生转 换却出现了转换。我们区分这两种错误类型，并为它们分配不同的状态。状态Di(i ∈{0, 1}) 表示由于延迟错误导致输出为错误值i的状态，Gi表示由于输出信号中出现毛刺所引起的 状态。表I总结了马尔可夫链（MC）模型的状态。

MC模型中的边表示状态之间的转移概率。为简便起见，我们仅显示误差情况下的边， 并假设输出幅度为0.5。一般而言，输出的幅值也会影响转移概率。此外，还存在隐式边， 它们是所示边的补集，并指向正确状态。例如，从C0到C1的隐式边是从C0到D0的边的 补集，因此具有相应的转移

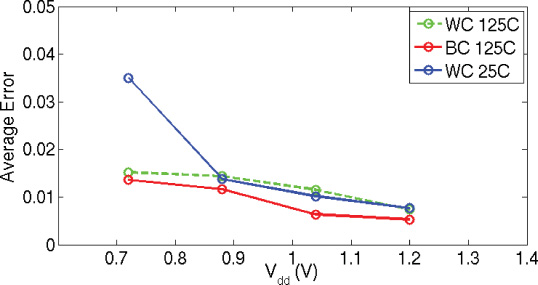
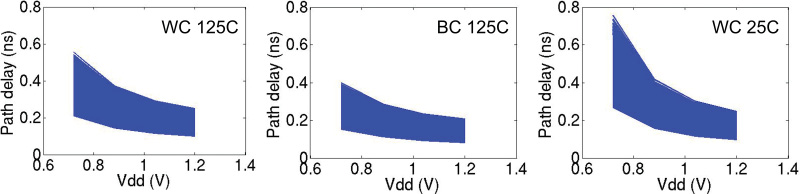
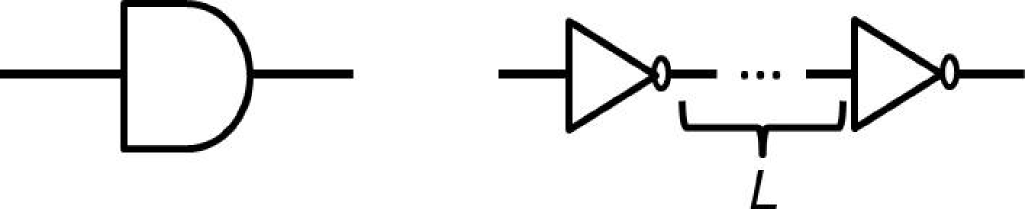
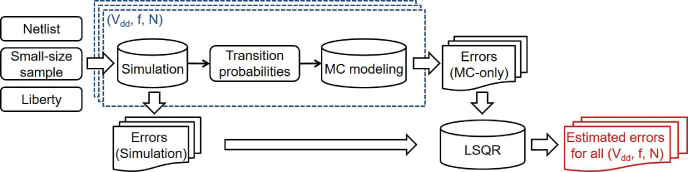
图10. 构建MC模型并估计不同工作点下计算误差的流程。

概率 1−pe1。例如，假设pe1= 0.1。这意味着如果电路处于状态C0，且下一个输出为1， 则由于延迟错误导致输出转换未被捕获的概率为10%，因此电路以概率pe1进入状态D0。其 余90%的情况下，转换成功完成，电路进入正确状态C1。

如果已知转移概率，那么我们可以求出MC的平衡概率（即稳态分布），进而评估相应 电路的精度。我们通过计算在电路输出端得到1的概率（即处于状态C1, D1,或G1,的概率）， 并将该概率与正确输出概率进行比较来实现这一目标。图10展示了我们的基于MC的误差估 计流程。我们通过生成一个小的输入样本集（从输入空间中均匀选择）并对电路进行仿真 来获得转移概率。我们基于门级网表执行逻辑仿真，然后收集MC模型不同状态之间转移速 率的统计信息。样本集的大小决定了仿真运行时间与构建的MC模型精度之间的权衡。我们 逐步增加输入样本大小，发现在我们的测试用例中，当输入样本大小小于或等于20时，转 移概率总是收敛（将样本大小增加到21并不会导致所收集数据发生显著变化）。因此，在 我们的实验中使用了20个输入样本。一旦估计出转移概率，我们就将其代入图9的MC模型， 并评估电路的精度。

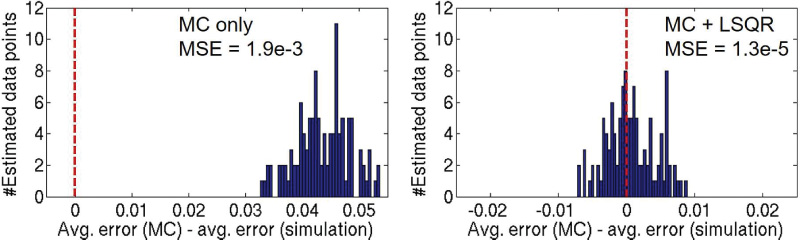
我们的实验结果表明，尽管我们蒙特卡洛模型（MC模型）估计的误差与仿真得到的 实际误差具有良好的相关性，但通常较为悲观。因此，我们应用最小二乘回归(LSQR)技术 来提高估计精度。LSQR步骤使用在仿真过程中观察到的最终误差值。进一步说明，我们 从可能输入的大空间中选取20个均匀分布的输入样本对电路进行仿真。我们从仿真中收集 两个数据集：(i) 用于构建MC模型的转移概率；(ii) 用于校正MC模型的最终误差值。图 11展示了一个示例，其中LSQR技术提高了估计精度。MC模型通过避免穷举仿真实现了快 速设计空间探索。请注意，每个(设计，工作点)组合仅需构建一次MC模型。

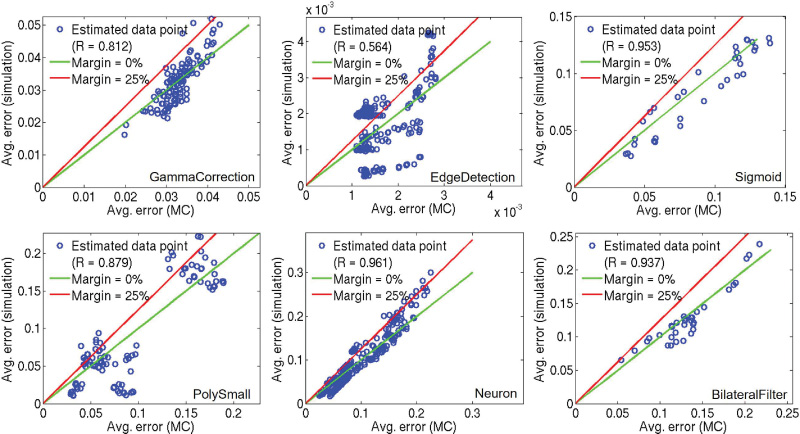
我们通过比较蒙特卡洛模型（即MC + LSQR）预测的平均误差值与布局后仿真结果来验 证建模流程。本文使用了六个具有代表性的测试用例，这些测试用例主要来自图像处理和人工 神经网络应用。测试用例列表见第5节。尽管蒙特卡洛模型在所有情况下均可使用，但它主要对 较大的测试用例（GammaCorrection [Qian et al. 2011], Neuron [Brown and Card 2001],Sigmoid 和 双边滤波器）更为有用，因为在这些情况下进行穷举仿真是耗时的。

在逻辑综合、布局和布线（SP&R）之后，每个测试用例在铿腾 NC‐Verilog 中进行仿真， 仿真时使用来自 SP&R 流程结果标注的延迟。为了展示蒙特卡洛模型在激进的电压和频率缩放 下预测误差的能力，该电路在 0.7V、最差工艺角、125◦C 条件下完成签核；然后在更低的电压 （dd={0.6, 0.64,…, 0.96}V）下运行，并提升时钟频率（例如，最高达到签核频率的 5×倍）。

图12显示，预测的平均误差与大多数测试用例的布局后仿真结果具有良好的相关性。 蒙特卡洛模型在小型测试用例（EdgeDetection和PolySmall）上的表现不佳，主要是因 为这些测试用例表现出确定性行为（尤其是EdgeDetection测试用例）。但如前所述，在 小型测试用例中蒙特卡洛模型可能并不适用，因为此时穷举仿真是可行且快速的。

在低误差情况下（例如Gamma校正），估计误差相对高于高误差情况（例如神经元）。 当跳变错误e0→1和e1→0非常小或非常大时，就会出现低误差情况。在这种情况下，电路 的行为几乎表现为确定性。例如，如公式(3)所述，当e0→1= e1→0= 1时，所有跳变均产 生误差，导致随机数的误差为零。我们的蒙特卡洛模型的主要局限性在于无法建模此类确 定性场景。

此外，如图12所示，蒙特卡洛误差估计存在一些差异。我们观察到，在大多数测试用 例中，25%裕量足以应对较大测试用例的差异。然而，这使得蒙特卡洛模型显得过于保守； 我们可能会舍弃一些可接受的工作点。正如第5节中所讨论的，使用蒙特卡洛模型并不总能 找到通过穷举仿真发现的最优工作点。尽管如此，我们认为蒙特卡洛模型在以下场景中仍 然有用：（i）估计无法进行穷举仿真的大型电路的误差；（ii）探索庞大的工作点空间。

为进一步阐明第二种情况，考虑在一个相对较大的电路上的MEOP问题，其errg oal=0.01。我们的方 法是搜索可能的

工作点，并选择一个满足errgoal且能耗最低的工作点。对于每个工作点，我们首先运行蒙 特卡洛模型以快速评估其误差行为。如果蒙特卡洛模型显示误差较高（例如0.1），则可以 安全地排除当前工作点并转向下一个。否则，我们对该工作点进行穷举仿真，以精确评估 其误差行为。因此，蒙特卡洛模型为许多工作点节省了宝贵的仿真时间。

4. 电路级优化

上一节讨论了一种场景，即随机计算电路已经实现，我们只能为其选择一个工作点，也就 是第2节中定义的MEOP问题。在本节中，我们考虑如何使用逻辑综合和物理设计技术来 优化电路，以提高其能效（SCOpt问题）。我们首先讨论随机计算电路的时序行为，并强 调误差产生的主要原因以及消除这些误差的机会（第4.1节）。然后我们讨论所提出的优化 方法（第4.2节）。

4.1. 到达时间错位 matters

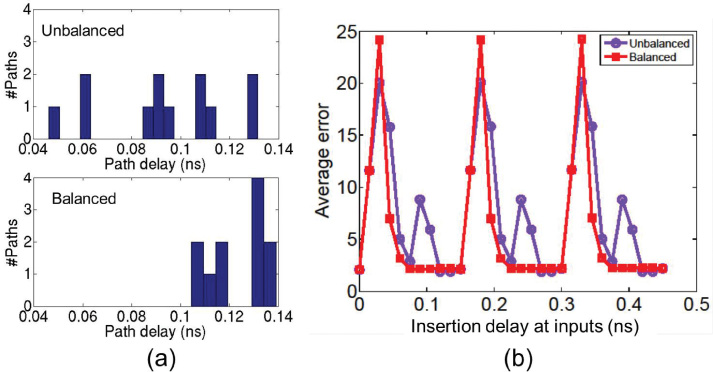
为了研究到达时间错位对SC电路计算精度的影响，我们在电路输入处插入延迟并逐渐增加； 如图13所示的例子中，我们将延迟从0ps扫描到450ps，即 3×时钟周期，步长为15ps。我 们记录平均计算误差的变化情况。该实验在测试用例PolySmall的两个实现上进行，其中 一个实现采用传统的P&R流程，另一个则经过优化以获得更平衡的路径延迟。图13(a)显示 了这两个实现的路径延迟分布。请注意，初始设计的最大路径延迟约为140ps。因此，由 于插入的输入延迟，这些设计将出现时序违规。

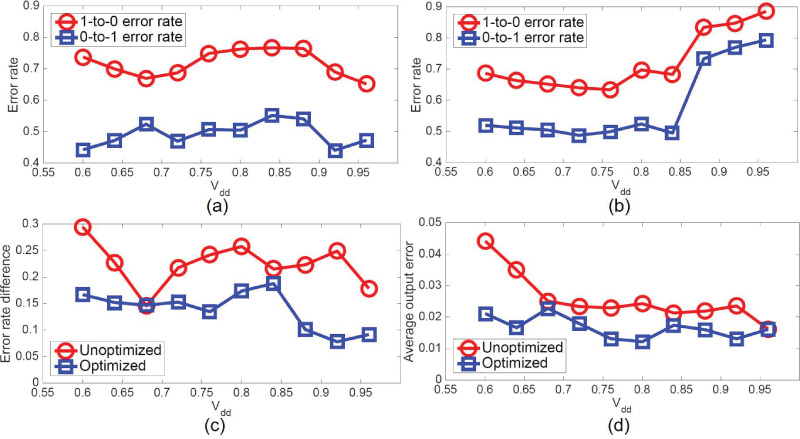
图13(b)中的结果表明，改变输入延迟会导致计算精度出现周期性波动，这说明了到达 时间与采样相位错位对计算精度的影响。更具体地说，当大量路径出现到达时间错位时， 例如在平衡情况下延迟介于15ps至65ps之间时，相应的计算误差较大。相反，当没有到达 时间错位时，例如在平衡情况下延迟介于60ps至150ps之间时，尽管该设计存在更大的时 序违规，但计算误差较小。此外，由于在不平衡情况下路径延迟范围更宽，因此不平衡实 现显示出更多非最小平均误差的数据点（如图13(b)所示）。因此，为了降低到达时间错位 的可能性并最小化计算误差，我们提出采用缓冲器插入和绕线方法来最小化SC电路中输入‐ 输出路径延迟差异。

4.2. 优化方法

为了解决到达时间错位问题，并在低电源电压或超频情况下减少计算误差，我们在SC电路 实现（即综合、布局与布线）过程中进行优化，以平衡电路的路径延迟。

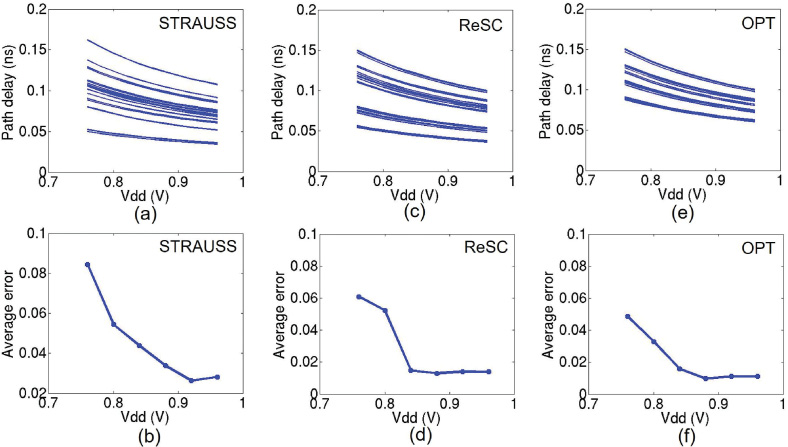
首先，我们考察两种主要的随机计算（SC）设计风格：随机电路综合中的谱变换应用 （STRAUSS）[Alaghi 和 Hayes 2015]以及 ReSC [钱等人 2011]。然后，我们比较它 们在给定范围的电源电压下的路径延迟和计算误差。图14 对比了在 28纳米全耗尽型绝缘 体上硅（FDSOI）技术下测试用例PolySmall 的 STRAUSS 和 ReSC。我们观察到，采用 ReSC 实现的 SC 电路相比 STRAUSS 设计的电路具有更平衡的路径延迟和更小的误差。 ReSC 架构由一个加法器和一个多路复用器组成，相对于电路的主输入而言非常对称。而 基于 STRAUSS 的电路则具有非对称结构，这使得它们比 ReSC 电路更小，但导致路径延 迟不平衡，从而对时序错误更为敏感。因此，在第5节报告的实验中，我们仅实现了基于 ReSC 的 SC 电路设计。

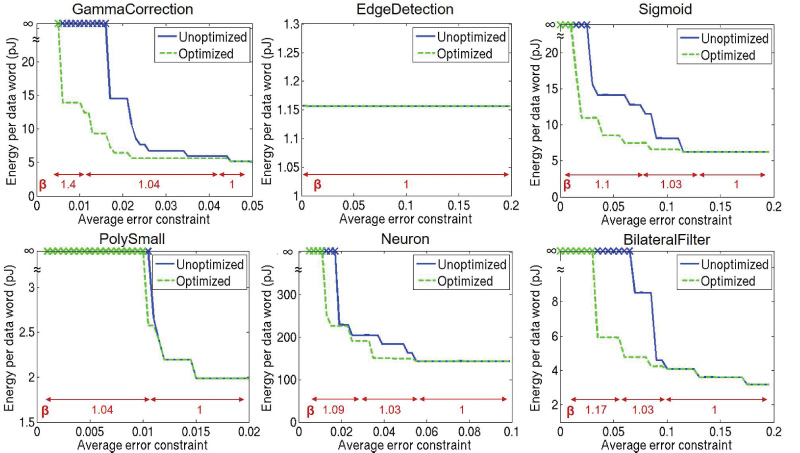、(c) 和 (e) 中的每条曲线表示具有唯一上升/下降转换组合的时序路径。[(a) 和 (b)] STRAUSS [Alaghi 和 Hayes 2012],[(c) 和 (d)] ReSC [钱等人 2011],以及 [(e) 和 (f)]使用我们提出的基于混合整数线性规划的方法优化的电路。)

为了优化电路，我们在布线后阶段进行缓冲器插入和/或绕线以平衡路径延迟。3以往 的研究文献中已应用多种数学规划方法来指导缓冲器插入和导线尺寸调整/绕线，以最小化 时钟偏斜或数据路径延迟 [Chu 和 Wong 1999；Han 等人 2015]。鉴于随机计算电路通 常规模较小，4我们构建了一个混合整数线性规划（MILP）模型，基于一组给定的缓冲候 选方案来搜索最优解。

我们将MILP表述如下。该优化的目标是最小化设计在给定电源电压范围内各时序路 径之间的归一化最大延迟差（用U表示）。约束条件为最大路径延迟和设计漏电功耗的上 界。公式中使用的符号见表II。

Minimize U, (4) subject to Di′k= Dk i+ ∑ 1 ≤ i ≤ M,1≤j ≤Q crj · dk j , (5)

我们注意到，缓冲器插入和绕线技术并非新颖。这些技术已被用于平衡时钟路径以最小化偏斜 [Han 等人 2015]， 以及平衡信号路径以防止智能卡中的功耗侧信道攻击 [Tiri 和 Verbauwhede 2006]。然而，据我们所知，我们 是首次将此类优化技术应用于随机计算电路中以平衡路径（数据路径）延迟，从而提高其精度的团队。典型的图 像处理随机计算电路仅有约20个门 [Alaghi 等人 2013],，而已知最大的随机计算电路不超过1,250个门实例 [ Li 和 Lilja 2011]。

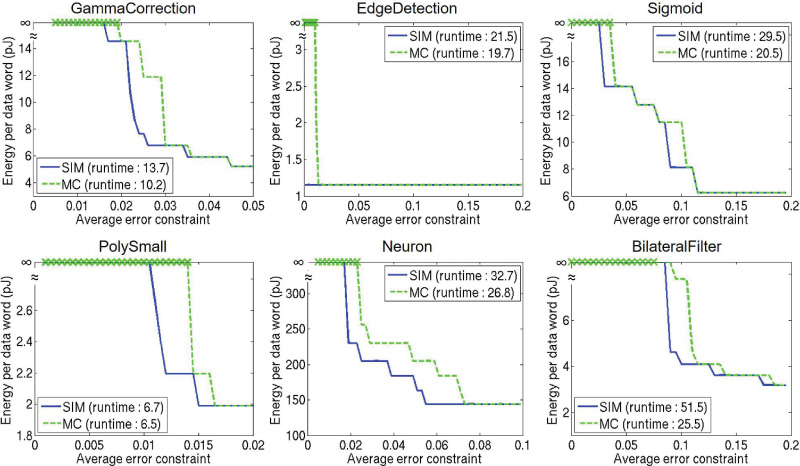
∑ 1≤j ≤Q crj ≤ 1, ∀ 1 ≤ r ≤ R, (6) Dk max= max 1≤i≤M Dk i, ∀ 1 ≤ k ≤ K, (7) α · Dk max ≥ D i′k, ∀ 1 ≤i ≤ M, 1 ≤ k ≤ K, (8) Dm′kax ≥ D i′k, ∀ 1 ≤i ≤ M, 1 ≤ k ≤ J, (9) Dm′kin ≤ D i′k, ∀ 1 ≤i ≤ M, 1 ≤ k ≤ K, (10) U ≥ DK max Dk max ·(Dm′kax − D m′kin), (11) β · Gk ≥ ∑ 1≤r≤R,1≤j ≤Q crj · gk j , 1 ≤ k ≤ K, (12) 其中，Di′k 是路径 Pi 在由 crj 指示的缓冲器插入和/或绕线迂回方案下的优化路径延迟。D m′kax 和 Dm′kin 分别是在电源电压 Vk 下考虑缓冲器插入和绕线迂回后的最大和最小路径延迟。 U 是所有电源电压下归一化路径延迟差值的上界。该混合整数线性规划模型通过最小化 U，从而最小化所有电源电压下的最大归一化路径延迟差值。此外，Gk 是原始设计的漏电 功耗。参数 gk j 是在电源电压 Vk 下进行缓冲器插入所引入的漏电功耗惩罚。我们的公式约 束了优化过程，使得在每个电源电压下的路径延迟不超过原始最大路径延迟的 α 倍，漏电 功耗不超过原始漏电功耗的 β 倍。

我们最初的研究尝试在优化过程中引入门尺寸调整和Vth交换。然而，这会导致我们的混 合整数线性规划优化的运行时间和复杂性显著增加，因为在所使用的技术中，每个门实例可能 有6到22种候选标准单元用于门尺寸调整和Vth交换。此外，微小的尺寸调整和/或Vth交换对路 径延迟的影响较小，因此并不具有明显效果

有助于平衡路径延迟。另一方面，大幅尺寸调整和/或Vth‐交换操作可能会导致最大电容和 最大转换违规，这是由于缩小尺寸和/或交换到更高的Vth时驱动能力弱，或增大尺寸时输 入引脚电容较大所致。因此，我们在优化中仅采用缓冲器插入和/或绕线。

图14(e)和(f)显示了优化的SC电路的最终路径延迟和计算误差。结果表明，相较于未 优化的STRAUSS和ReSC实现，性能有显著提升。

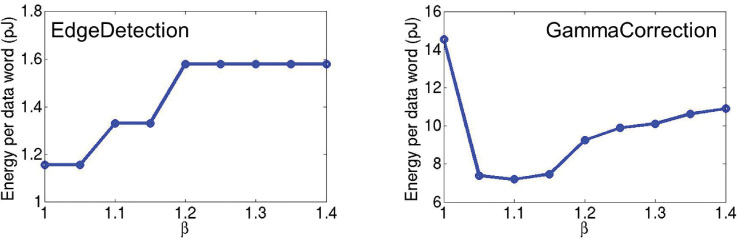
在由于插入的缓冲器和导线段导致的功耗开销与因更平衡的路径延迟而提高精度所带 来的能量收益之间存在权衡（例如，更平衡的路径延迟能够实现更大的供电电压降标）。 仅当电压降标带来的功耗收益超过插入的缓冲器和导线段所引起的功耗开销时，我们的优 化才能降低能量。具有简单网表结构的小型设计可能已经具备相对平衡的路径延迟，并且 对缓冲器插入的功耗开销敏感（即，缓冲器插入的相对功耗开销较大），因此该类设计从 我们优化中获得的潜在收益较小。另一方面，在大型设计中，缓冲器插入引起的功耗开销 相对于总设计功耗而言相对较小。因此，大型设计更有可能从我们的优化中受益。图15展 示了在给定精度要求（即，errgoal= 0.02）下，不同 β值优化后的设计能耗。我们观察到， 对于小型测试用例EdgeDetection（包含∼5个实例），较大的 β值始终会增加设计能耗。 5而对于具有 ∼100个实例的较大的测试用例GammaCorrection，随着 β值的变化，设计 能耗呈现出单峰行为，这是由于缓冲器插入的功耗开销与精度提升带来的能量收益之间的 权衡所致。这些结果支持了我们的直觉：大型设计更有可能从优化中获益。

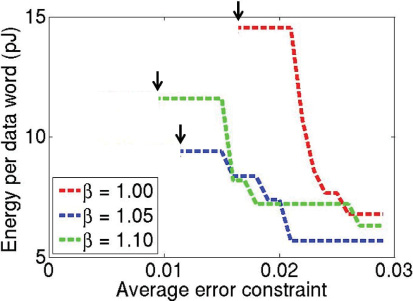
图16比较了在不同精度要求下测试用例GammaCorrection的能耗，该测试用例使用 不同的 β值进行优化。图16中的黑色箭头表示每个优化电路可达到的最小误差。我们观察 到，较大的 β值能够带来更高精度。然而，由于缓冲器插入和绕线带来的功耗开销与精度 提升带来的能量收益之间存在权衡，较高的 β值并不一定能够提供更小的设计能耗。因此， 我们对 β值进行扫描，以探索这种权衡并最小化设计能耗。该优化过程如算法1所示，其中 我们

迭代地将 β的值增加 δ（在我们的实验中为 δ= 0.05），直到不再有进一步的能耗降低。

算法1： 随机电路优化。

1: β ← 1；能量 ← inf；被v改进 ← true
2: 当被v改进时 do
3: 求解混合整数线性规划； 执行缓冲器插入和/或绕线作为工程变更指令
4: 执行穷举仿真以搜索每个 errgoal 的最小能量工作点
5: 计算所有 errgoal 上的平均能量；更新能量
6: β ← β+ δ
7: 如果能量降低则
8: 被v改进 ← true
9: 否则
10: 被v改进 ← false
11: 结束 if
12: 结束 while

为了评估工艺角和温度变化的影响，我们使用新思科技SiliconSmart [新思科技 2014]在不同工艺角（最坏工艺角和最佳工艺角）以及不同温度（125◦C 和 25◦C）下对标 准单元库进行表征。我们选择相同的伽马校正测试用例，并在不同的电源电压下仿真电路。 结果如图17所示。当电源电压从1.2V降至0.72V时，各工艺角之间的差异在60%以内（相 对于相同电压下的最大误差进行归一化），这导致输出误差的最大变化为5%。

图18进一步显示了在不同工艺角下各种电源电压的路径延迟。我们观察到，由于门延 迟较小，最佳工艺角情况下的最大路径延迟差异减小，从而导致误差更小。此外，较低的 温度会增加最大路径延迟差异（温度反转效应），尤其是在低电源电压下，与默认情况 （最坏工艺角125◦C）相比，会导致更大的误差。

为了确保工程变更指令（ECOs）的可行性，我们根据具有不同输入斜率和负载电容值的缓冲器插入 和/或绕线候选情况对查找表（LUT）进行表征。然后我们建立相应的混合整数线性规划（MILP）模型

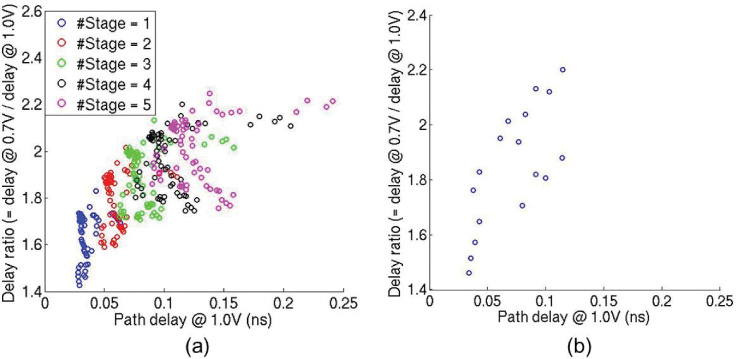
基于特征化的查找表优化电路。该方法与Han等人[2015]的方法类似。为了在一系列电源 电压下平衡路径延迟并最小化混合整数线性规划运行时间，我们选择覆盖广泛延迟‐电压权 衡但候选数量较少的缓冲器插入和/或绕线迂回方案。我们研究了不同门类型、门尺寸、阈 值电压和导线长度下的延迟‐电压权衡。我们观察到，延迟‐电压权衡受阈值电压、门尺寸和 导线长度的影响显著，这与Chan和Kahng[2012]的观察结果一致。因此，我们采用两种 缓冲方式——单级非反相缓冲器以及中间带有绕线迂回的反相器对，如图19所示。我们的 方法根据延迟需求从多种尺寸的缓冲器和反相器中进行选择。我们同时使用低Vth（LVT） 和常规Vth（RVT）单元。迂回导线长度L的范围为 10μm至 50μm，步长为 10μm。基 于查找表，我们进一步扩展了多级单元结构的缓冲候选方案（例如五级X100缓冲器），以 覆盖广泛的延迟范围。然而，大量的缓冲候选方案会显著增加混合整数线性规划的运行时 间。因此，我们对候选方案进行剪枝，使得在一定的延迟及延迟‐电压权衡范围内，将解空 间均匀划分为 4×4个子区域，然后从中选择缓冲方案。

从每个子区域中选择漏电功耗最小的解。图20(a)展示了最多包含五级缓冲候选方案的解空 间。图20(b)展示了剪枝后的缓冲候选方案，其延迟范围为20ps到120ps。我们的实验表明， 剪枝显著减少了运行时间，同时对解的质量造成的影响可以忽略不计。6

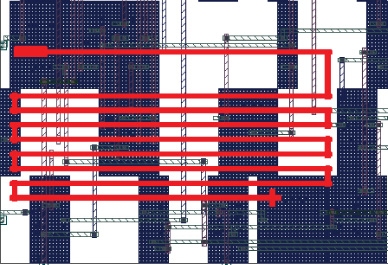
使用混合整数线性规划解，我们执行缓冲器插入和绕线迂回作为工程变更步骤。鉴于 单级非反相缓冲器插入较为简单，我们使用布局布线工具中的ECO命令来完成缓冲器插入 和布局合法化。对于带绕线迂回的反相器对插入，我们执行算法2中描述的ECO步骤。在 设计流程中，我们首先插入第一个反相器。然后合法化所插入反相器的位置，以留出足够 的空间用于走线迂回，例如将反相器移离模块边界，并确保与先前的绕线迂回无重叠。接 着插入第二个反相器，使其相对于第一个反相器在水平方向上相距25个站点，垂直方向上 相隔两行。最后，在两个反相器之间，依据M3和M4层上的单宽双间距（1W2S）布线规 则执行绕线迂回。图21展示了绕线迂回的一个示例。我们当前的优化方法尚未考虑翻转活 动信息。然而，功能感知和输入模式感知优化将成为我们未来的研究方向之一。

算法2： 反相器对插入流程。

1：放置第一个反相器
2：合法化第一个反相器的位置
3：插入第二个反相器，使其与第一个反相器在水平方向上相距25个位置，在垂直方向上相距两行
4：使用单宽双间距进行布线迂回

对于具有 ∼500个门实例的最大设计，在24核2.5GHz的英特尔至强服务器上，混合整数线性规划运行时间少于20秒。 ACM期刊计算系统新兴技术期刊，第13卷第3期，文章47，出版日期：2017年4月

5. 实验结果

实验基于28纳米全耗尽型绝缘体上硅技术实现。我们使用SynopsysDesign Compiler vH2013.03-SP3[Synopsys 2013a],综合测试用例，并使用Synopsys IC Compiler vI-2013.12-SP1[ Synopsys 2013b]进行布局布线。我们分别使用Sy nopsy s PrimeTime vH-2013.06-SP2[Synopsys 2013c]和Synopsys PT-PXvH-2013.06-SP2进行时序和功耗分析。我们使用Cadence NC-Verilog v8.2[Cadence 2011]进行门级仿真。我们使用MATLAB R2013a[MathWorks 2013]构建马尔可 夫链模型。在优化流程中使用的混合整数线性规划求解器是CPLEX v12.5[IBM 2013]。我们的测试 用例（见表III）是从随机计算文献中选取的代表性电路，应用于图像处理和神经网络设计等典型场 景。在输入生成方面，我们通过SNG将二进制输入向量转换为伪随机比特流。

5.1. 电路优化结果

为了评估我们优化方法的有效性，将其应用于表III中的测试用例，并将结果与未优化电路 进行比较。例如，图22展示了我们的优化方法如何改变GammaCorrection测试用例的0 到1和1到0的错误率。同时表明，即使错误率有所增加，降低两种错误率之间的差异仍可实 现输出误差减少。例如，在电压范围Vdd= 0.88–0.96V下，我们看到优化电路的0到1和1 到0错误更多。图23所示的最终结果也证实了优化电路的误差降低；即在应用相同精度约 束的情况下，优化电路每单位数据消耗的能量更低。然而，由于优化电路的错误率差异小 于未优化电路，因此我们观察到优化电路具有更好的输出误差行为。

图23显示了每个设计在满足给定平均误差约束errgoal（在可能的工作点空间内）时所 需的最小能量。交叉符号(×)表示对于给定的errgoal未找到合适的工作点。注意，具有大量 插入缓冲器（更平衡的路径延迟）的电路在误差约束较高时可能由于电压调节而具有较低 的能耗，但在误差约束较低时可能由于插入缓冲器带来的功率惩罚而导致较高的能耗。因 此，很难找到一个能在所有误差约束下均实现最小能量的优化电路。为解决此问题，我们 考虑多个优化电路，每个电路使用不同的 β值进行优化。请注意，我们在图23中展示了不 同的优化电路以说明我们的优化性能。设计人员可以根据自身的精度要求选择合适的条件， 并使用我们的方法找到符合其需求的优化电路。此外，我们的优化还支持