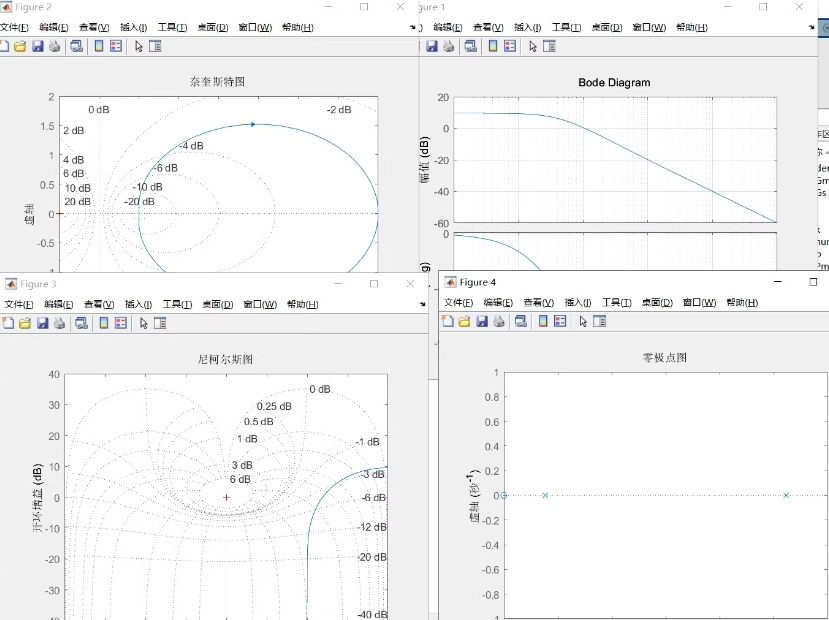
控制系统的频域响应和稳定性分析。频率响应伯德图，奈奎斯特图，尼克斯图，零极点图，求解幅值裕度，相位裕度，剪切频率，并根据系统的频域响应分析系统的稳定性。

控制系统的频域响应和稳定性分析。频率响应伯德图，奈奎斯特图，尼克斯图，零极点图，求解幅值裕度，相位裕度，剪切频率，并根据系统的频域响应分析系统的稳定性。

控制系统的频域响应和稳定性分析是经典控制理论中的重要内容。通过频域分析方法，可以直观地评估系统的动态性能和稳定性。以下是关于频率响应、伯德图（Bode Plot）、奈奎斯特图（Nyquist Plot）、尼克斯图（Nichols Plot）、零极点图的介绍，以及如何计算幅值裕度、相位裕度、剪切频率，并基于这些指标分析系统稳定性。

---

1. 理论基础

（1）频率响应

• 频率响应描述了线性时不变系统在正弦输入下的稳态输出特性。
• 通常用传递函数 $ G(s) $ 表示，令 $ s = j\omega $，得到频率响应 $ G(j\omega) $。

（2）伯德图（Bode Plot）

• 包括幅频特性曲线和相频特性曲线。
• 幅频特性：以对数坐标表示增益 $ |G(j\omega)| $。
• 相频特性：表示相位角 $ \angle G(j\omega) $。

（3）奈奎斯特图（Nyquist Plot）

• 绘制 $ G(j\omega) $ 在复平面上的轨迹。
• 用于分析系统的稳定性和闭环系统的特性。

（4）尼克斯图（Nichols Plot）

• 将伯德图的幅值和相位信息结合在一个图中。
• 常用于设计控制器。

（5）零极点图

• 显示传递函数的零点和极点分布。
• 极点位置决定了系统的稳定性。

（6）幅值裕度和相位裕度

• 幅值裕度：系统达到不稳定状态时，增益还能增加的倍数。
• 相位裕度：系统达到不稳定状态时，相位还能延迟的角度。

（7）剪切频率

• 系统增益为 1（0 dB）时对应的频率。

（8）稳定性分析

• 根据奈奎斯特判据或伯德图的幅值裕度和相位裕度判断系统稳定性：
  • 如果幅值裕度 > 1 或相位裕度 > 0°，系统稳定。
  • 否则，系统不稳定。

---

2. Python 实现

以下是一个完整的 Python 示例代码，使用 control 和 matplotlib 库进行分析。

import numpy as np
import matplotlib.pyplot as plt
import control as ctrl

# 定义传递函数
num = [1]  # 分子系数
den = [1, 2, 1]  # 分母系数
sys = ctrl.TransferFunction(num, den)

# （1）绘制伯德图并计算幅值裕度和相位裕度
mag, phase, omega = ctrl.bode_plot(sys, dB=True, Hz=True, deg=True)
gm, pm, wcg, wcp = ctrl.margin(sys)  # 计算幅值裕度、相位裕度、剪切频率等

print(f"幅值裕度 (Gain Margin): {gm:.2f}")
print(f"相位裕度 (Phase Margin): {pm:.2f}°")
print(f"增益交越频率 (Gain Crossover Frequency): {wcg:.2f} rad/s")
print(f"相位交越频率 (Phase Crossover Frequency): {wcp:.2f} rad/s")

# （2）绘制奈奎斯特图
plt.figure()
real, imag, freq = ctrl.nyquist_plot(sys, plot=True)
plt.title("Nyquist Plot")
plt.grid()

# （3）绘制尼克斯图
plt.figure()
ctrl.nichols_plot(sys)
plt.title("Nichols Plot")
plt.grid()

# （4）绘制零极点图
plt.figure()
ctrl.pzmap(sys, plot=True)
plt.title("Pole-Zero Map")
plt.grid()

# （5）稳定性分析
poles = ctrl.pole(sys)  # 获取系统的极点
if all(poles.real < 0):
    print("系统稳定")
else:
    print("系统不稳定")

plt.show()

—

3. 结果解释

（1）伯德图

• 幅频曲线显示了系统增益随频率的变化。
• 相频曲线显示了系统相位随频率的变化。
• 幅值裕度和相位裕度可以直接从伯德图中读取。

（2）奈奎斯特图

• 系统是否稳定可以通过奈奎斯特轨迹是否包围 (-1, 0) 点来判断。

（3）尼克斯图

• 将幅值和相位结合在一起，便于观察系统的动态特性。

（4）零极点图

• 极点位于左半平面时，系统稳定；否则不稳定。

（5）稳定性分析

• 如果所有极点的实部小于 0，则系统稳定。

---

4. 注意事项

1. 库安装：确保已安装 control 和 matplotlib 库。

   pip install control matplotlib
   

2. 单位转换：注意频率单位（rad/s 或 Hz）和角度单位（弧度或度）。
3. 数值精度：对于高阶系统，计算结果可能会有误差，需谨慎处理。

---

以上代码和分析方法可以帮助你全面了解控制系统的频域响应和稳定性。