以下程序会输出什么?
#include <stdio.h>
int main()
{
char a= -1;
signed char b=-1;
unsigned char c=-1;
printf(“a=%d,b=%d,c=%d”,a,b,c);
return 0;
}
相信很多朋友看到这道题后有所疑惑:这能有什么问题,输出应该是-1,-1,-1呀?

这种疑惑便是今天要讲到的细节知识。
其实它的答案是-1 -1 255.

为了便于理解,我们先讲解数据类型:
数据类型
| char | 字符数据类型 1byte |
| short | 短整型 2byte |
| int | 整型 4byte |
| long | 长整型 4/8byte |
| long long | 更长的整型 8byte |
| float | 单精度浮点数 4byte |
| double | 双精度浮点数 8byte |
long: 在32位机器下是4byte,在64位机器下是8byte.
整型家族
按照有无符号来分类:
| char | unsigned char signed char |
| short | unsigned short signed short |
| int | unsigned int signed int |
| long | unsigned lnog signed long |
| long long | unsigned long long[int] signed long long[int] |
特殊点:字符的本质是ASCII值,所以属于整形。除此之外,char到底是unsigned char还是signed char是标准为定义的,但大部分编译器,如VS下默认是有这两种类型区分的。
这里提出疑问:有无符号的区分有什么意义呢?
1.为了创建变量的时候符合实际情况。比如身高、体重没有负值。
2.有无符号决定了数值二进制位最高位的0或1具有符号意义还是数值意义。
步入正题,整形数据在内存中到底是如何存储的?
整形数据在内存中如何存储?
整形数据在内存存放的是二进制,并且是数据的补码,但调试的过程中我们看到的又是16进制数,这里不要混淆,是因为如果以二进制位显示数据过长,为了便于观察采取16进制显示。
举例:
十进制的21:
二进制表示:0b10101
八进制表示:025
十进制表示:21
十六进制表示:0x15
为什么数据在内存中必须是补码存储呢?
在计算机系统中,数值一律用补码来表示和存储。原因在于,使用补码,可以将符号位和数值域统
一处理;
同时,加法和减法也可以统一处理(CPU只有加法器)此外,补码与原码相互转换,其运算过程
是相同的,不需要额外的硬件电路。
举例:
我们要计算1+(-1):
如果以两者的原码进行计算(假设数据是8位):
1的原码: 0000 0001
-1的原码:1000 0001
结果为: 1000 0001——>-2 显然是错的.
如果以两者的补码进行计算(假设数据是8位):
1的补码: 0000 0001
-1的补码:1111 1111
结果为: 1 0000 0000——>最高位1溢出,最终得到0正确.
针对最开始的题,我们还需要了解数据表示范围:
数据范围
char型:
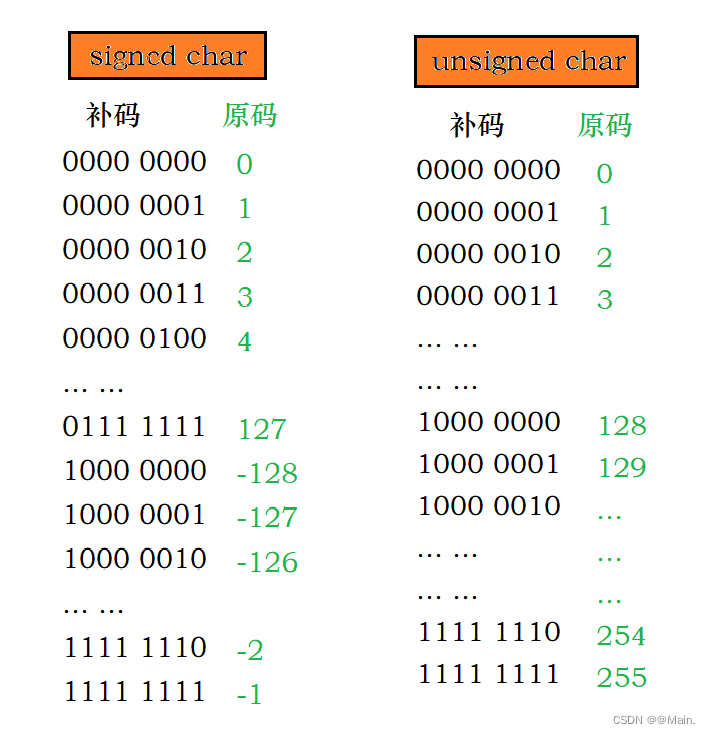
如图为char型数据可表示范围:
有符号的:-127~128
无符号的:0~255
其他类型同理.
至此,我们可以讲解起初的题了.(先文字讲解,后图解)
首先题中开始赋值时给字符a,b,c都赋的是整形数值(32bit);
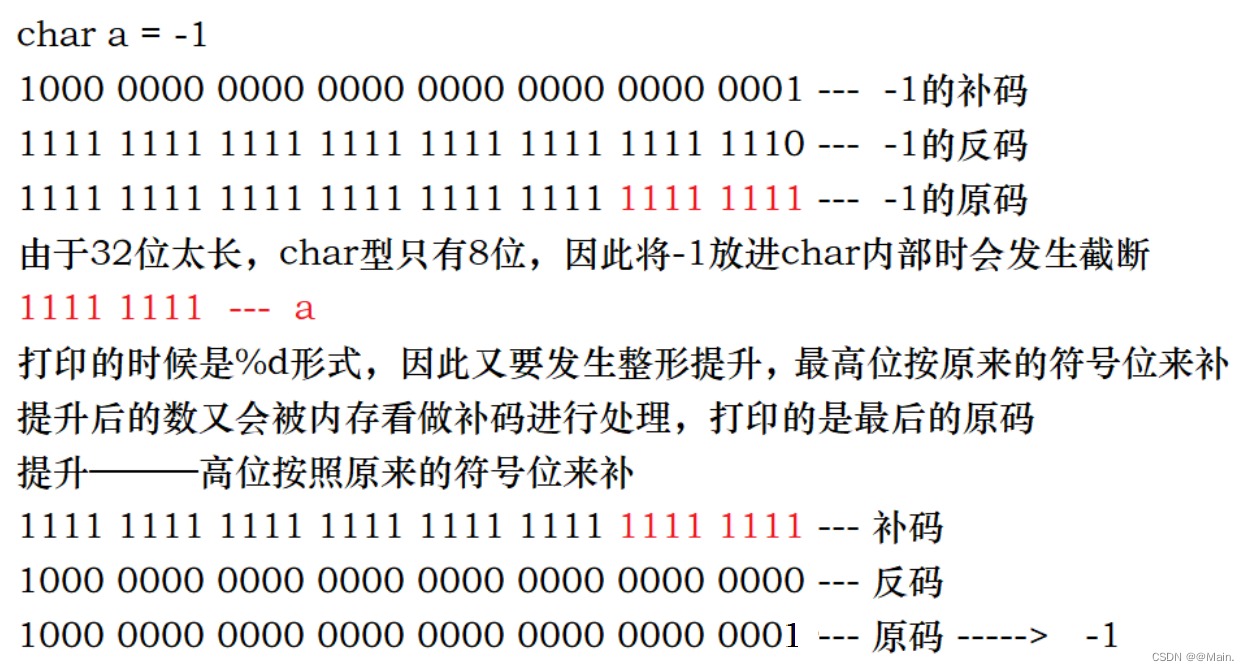
char a = -1
1000 0000 0000 0000 0000 0000 0000 0001 — -1的补码
1111 1111 1111 1111 1111 1111 1111 1110 — -1的反码
1111 1111 1111 1111 1111 1111 1111 1111 — -1的原码
由于32位太长,char型只有8位,因此将-1放进char内部时会发生截断
1111 1111 — a
打印的时候是%d形式,因此又要发生整形提升,
提升后的数又会被内存看做补码进行处理,打印的是最后的原码
提升———高位按照原来的符号位来补
1111 1111 1111 1111 1111 1111 1111 1111 — 补码
1000 0000 0000 0000 0000 0000 0000 0000 — 反码
1000 0000 0000 0000 0000 0000 0000 0001 — 原码 -----> -1
unsigned char c = -1
1000 0000 0000 0000 0000 0000 0000 0001 — -1的补码
1111 1111 1111 1111 1111 1111 1111 1110 — -1的反码
1111 1111 1111 1111 1111 1111 1111 1111 — -1的原码
继续截断,再整型提升
1111 1111 — c
0000 0000 0000 0000 0000 0000 1111 1111 — 补码 <=> 原码
结果为255
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








