归并排序（递归）

1.概念

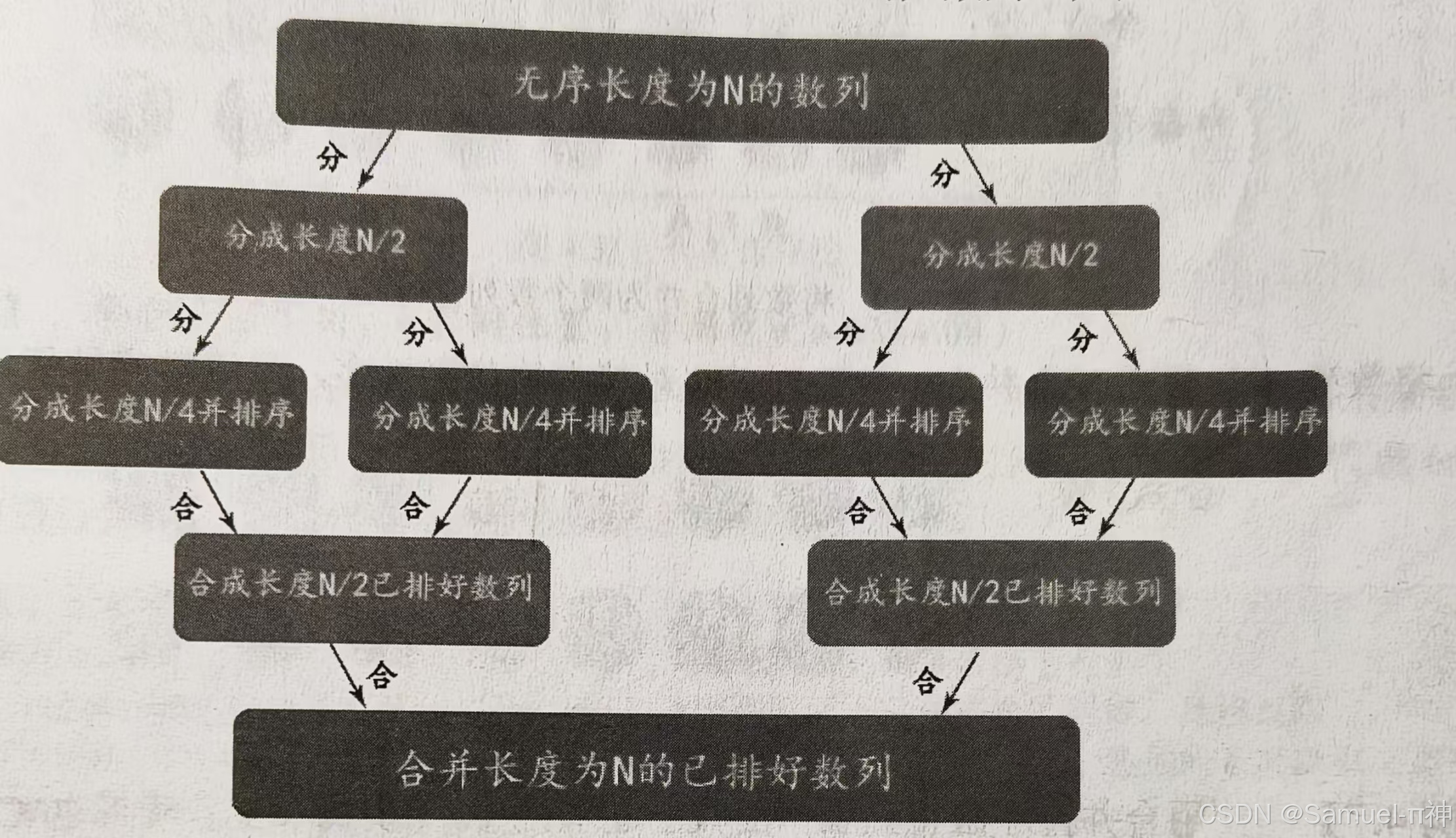
归并排序法是针对已经排好的两个或两个以上的数列，通过合并的方式，将其组合成一个有序的大数列。使用归并排序法为一个数列排序时，首先将无序的数列分成若干小份。分若干分的规则就是不断把每段长度除以2（对半分），直到分到不能再分为止，然后对最小分进行排序，最后再逐步合并成一个有序的大数列。

2.代码

def merge_sort(data):
    if len(data)<=1:
        return data
    # 递归终止条件，即长度小于等于1时，不再进行分割直接返回

    mid=len(data)//2
    left=data[:mid]
    right=data[mid:]
    left=merge_sort(left)
    right=merge_sort(right)
    # 运用递归对两部分进行分割，并执行排序操作

    result=[]
    # 创建一个空列表 result 用于存储排序结果。

    while left and right:
    # 当 left 和 right 都不为空时，比较它们的第一个元素。

        if left[0]<=right[0]:
            result.append(left.pop(0))
    # 如果 left 的第一个元素小于或等于 right 的第一个元素，
    # 将 left 的第一个元素添加到 result 中，并使用 pop(0) 从 left 中移除该元素。
        else:
            result.append((right.pop(0)))
    # 否则，将 right 的第一个元素添加到 result 中，并使用 pop(0) 从 right 中移除该元素。

    if left:
        result+=left
    # 如果 left 不为空，将 left 中的剩余元素添加到 result 中。
    if right:
        result+=right
    # 如果 right 不为空，将 right 中的剩余元素添加到 result 中。
    return result

data=[34,45,33,5,24,66,9,2]
print(merge_sort(data))

3.过程解释

初始：data = [34, 45, 33, 5, 24, 66, 9, 2]
mid = 4，left = [34, 45, 33, 5]，right = [24, 66, 9, 2]。
    递归调用：
    merge_sort([34, 45, 33, 5])：
    mid = 2，left = [34, 45]，right = [33, 5]。
        递归调用：
        merge_sort([34, 45])：
        mid = 1，left = [34]，right = [45]。
        排序后：[34] 和 [45] 合并为 [34, 45]。
        merge_sort([33, 5])：
        mid = 1，left = [33]，right = [5]。
        排序后：[5, 33]。
        合并 [34, 45] 和 [5, 33]：
比较 34 和 5，添加 5 到 result，result = [5]。
比较 34 和 33，添加 33 到 result，result = [5, 33]。
剩下 34 和 45，添加 34 和 45 到 result，result = [5, 33, 34, 45]。

merge_sort([24, 66, 9, 2])：
mid = 2，left = [24, 66]，right = [9, 2]。
    递归调用：
    merge_sort([24, 66])：
    mid = 1，left = [24]，right = [66]。
    排序后：[24, 66]。
    merge_sort([9, 2])：
    mid = 1，left = [9]，right = [2]。
    排序后：[2, 9]。
    合并 [24, 66] 和 [2, 9]：
    比较 24 和 2，添加 2 到 result，result = [2]。
    比较 24 和 9，添加 9 到 result，result = [2, 9]。
    剩下 24 和 66，添加 24 和 66 到 result，result = [2, 9, 24, 66]。

合并：
合并 [5, 33, 34, 45] 和 [2, 9, 24, 66]：
比较 5 和 2，添加 2 到 result，result = [2]。
比较 5 和 9，添加 5 到 result，result = [2, 5]。
比较 33 和 9，添加 9 到 result，result = [2, 5, 9]。
比较 33 和 24，添加 24 到 result，result = [2, 5, 9, 24]。
比较 33 和 66，添加 33 到 result，result = [2, 5, 9, 24, 33]。
剩下 34 和 66，添加 34 到 result，result = [2, 5, 9, 24, 33, 34]。
剩下 45 和 66，添加 45 到 result，result = [2,5,9,24,33,34,45]。
剩下 66，添加 66 到 result，result = [2, 5, 9, 24, 33, 34, 45, 66]。

# 为了更容易看出过程，可以在代码执行过程中
# 输出每一次的结果并在结果处做上标记
def merge_sort(data):
    if len(data)<=1:
        return data
    mid=len(data)//2
    left=data[:mid]
    right=data[mid:]
    left=merge_sort(left)
    right=merge_sort(right)
    result=[]
    while left and right:
        if left[0]<=right[0]:
            result.append(left.pop(0))
            print(result)
            print("-"*20)
        else:
            result.append((right.pop(0)))
            print(result)
            print("=" * 20)
    if left:
        result+=left
        print(result)
        print('*'*20)
    if right:
        result+=right
        print(result)
        print('^'*20)
    return result
data=[34,45,33,5,24,66,9,2]
merge_sort(data)

# 输出结果：
# [34]
# --------------------
# [34, 45]
# ^^^^^^^^^^^^^^^^^^^^
# [5]
# ====================
# [5, 33]
# ********************
# [5]
# ====================
# [5, 33]
# ====================
# [5, 33, 34, 45]
# ********************
# [24]
# --------------------
# [24, 66]
# ^^^^^^^^^^^^^^^^^^^^
# [2]
# ====================
# [2, 9]
# ********************
# [2]
# ====================
# [2, 9]
# ====================
# [2, 9, 24, 66]
# ********************
# [2]
# ====================
# [2, 5]
# --------------------
# [2, 5, 9]
# ====================
# [2, 5, 9, 24]
# ====================
# [2, 5, 9, 24, 33]
# --------------------
# [2, 5, 9, 24, 33, 34]
# --------------------
# [2, 5, 9, 24, 33, 34, 45]
# --------------------
# [2, 5, 9, 24, 33, 34, 45, 66]
# ^^^^^^^^^^^^^^^^^^^^