论文阅读 | CVPR | MambaOut：视觉任务真的需要 Mamba 吗？

论文阅读 | CVPR | MambaOut：视觉任务真的需要 Mamba 吗？

题目：MambaOut: Do We Really Need Mamba for Vision?
会议：IEEE Conference on Computer Vision and Pattern Recognition（CVPR）
论文：https://doi.org/10.48550/arXiv.2405.07992
代码：https://github.com/yuweihao/MambaOut?tab=readme-ov-file
年份：2025

摘要

提出MambaOut模型：

• 与卷积模型和基于注意力的模型相比，Mamba 在视觉任务上的表现往往不尽人意。
• 结论：Mamba非常适合具有长序列和自回归特性的任务。
• 对于视觉任务而言:
  图像分类任务并不具备这两个特性（长序列和自回归特性），因此假设 Mamba对于该任务并非必需；
  检测和分割任务虽然不是自回归的，但具有长序列特性；
• 构建名为 MambaOut 的模型，这些模型通过堆叠 Mamba块并去除其核心令牌混合器 SSM 得到。
  

图 1（a）门控卷积神经网络（Gated CNN）和Mamba 模块的架构（省略了归一化层和残差连接）。Mamba模块在门控卷积神经网络的基础上增加了一个状态空间模型（SSM）从而进行了扩展。对于ImageNet上的图像分类任务来说，状态空间模型并非是必需的。堆叠门控卷积神经网络模块来构建一系列名为MambaOut的模型。

• MambaOut 模型在 ImageNet 图像分类任务上超越了所有视觉 Mamba 模型，这表明 Mamba 对于该任务确实并非必要。

引言

• 本文从概念上总结出 Mamba 非常适合具有两个关键特性的任务：长序列和自回归特性。 这是由于 SSM 固有的 RNN机制（详见图 2 和图 3 的解释）。

• 文中提出，具备这长序列和自回归的视觉任务并不多：
  以 ImageNet图像分类任务为例，它既不符合长序列特性，也不符合自回归特性；
  COCO 数据集上的目标检测与实例分割任务与ADE20K数据集上的语义分割任务，仅符合长序列特性。

  • 注释1：自回归特性要求每个令牌仅从前面的令牌和当前令牌聚合信息，这种令牌混合方式被称为因果模式（见图 2 (a)）。
    

图 2：从内存角度展示因果注意力机制和类循环神经网络（RNN）模型的机制示意图，其中 $x_i$ 表示第i步的输入令牌。(a) 因果注意力将前面所有令牌的键 $k$ 和值 $v$ 存储为内存。通过不断添加当前令牌的键和值来更新内存，因此这种内存是无损的，但缺点是随着序列变长，整合旧内存和当前令牌的计算复杂度会增加。因此，注意力机制能有效地处理短序列，但在处理长序列时可能会遇到困难。(b) 相比之下，类 RNN 模型将前面的令牌压缩为固定大小的隐藏状态 $h$，以此作为内存。这种固定大小意味着 RNN 的内存本质上是有损的，无法直接与注意力模型的无损内存容量相媲美。尽管如此，类 RNN 模型在处理长序列时可以展现出明显的优势，因为无论序列长度如何，将旧内存与当前输入合并的复杂度保持不变。

• 文中提出，所有视觉识别任务都属于理解范畴，而非生成范畴，这意味着模型可以一次性看到整个图像。 因此，在视觉识别模型的令牌混合过程中施加额外的因果约束可能会导致性能下降（见图 2 (b)）。

• 基于上述概念性讨论，我们提出以下两个假设：

  • 假设 1：由于 ImageNet 图像分类任务既不符合长序列特性，也不符合自回归特性，因此 SSM 对于该任务并非必要。

  • 假设 2：虽然目标检测与实例分割任务以及语义分割任务不具有自回归特性，但它们符合长序列特性，因此 SSM 可能对这些任务具有潜在益处。

• 为了通过实验验证假设，开发了一系列名为 MambaOut 的模型，这些模型通过堆叠门控卷积神经网络（Gated CNN） [18] 块构建而成。Gated CNN 块和 Mamba 块的关键区别在于是否存在 SSM，如图 1 (a) 所示。

• 实验结果表明，更为简单的 MambaOut 模型在实际应用中已经超越了视觉 Mamba 模型的性能，这反过来验证了我们的假设 1。
  

图 1 (b) 在 ImageNet 图像分类任务上，MambaOut 的性能优于视觉 Mamba 模型，例如 Vision Mamba 、VMamba 和 PlainMamba 。

• 还通过实验结果表明，在检测和分割任务中，MambaOut 的性能不及当前最先进的视觉 Mamba 模型，这凸显了 SSM 在这些任务中的潜力，有效地验证了我们的假设 2。

创新点

本文的贡献主要体现在三个方面：

• 第一，分析了 SSM 类 RNN 的机制，从概念上得出 Mamba 适合具有长序列和自回归特性任务的结论。
• 第二，研究了视觉任务的特性，并假设由于 ImageNet 图像分类任务不满足上述两个特性，因此 SSM对于该任务并非必要；而对于检测和分割任务，尽管它们不具有自回归特性，但由于符合长序列特性，探索 SSM 在这些任务中的潜力仍然具有价值。
• 第三，我们开发了一系列基于 Gated CNN 块但不含 SSM 的 MambaOut 模型。它很可能成为未来视觉 Mamba模型研究的自然基线。

概念讨论

1. Mamba 的令牌混合器是SSM ( 选择性状态空间模型 ) ，它定义了四个与输入相关的参数$（\Delta ,A,B,C）$，并通过以下公式将它们转换为$（\overline{A},\overline{B},C）$：

   $$\begin{gathered} \overline{A}=\exp (\Delta A) \\ \overline{B}=(\Delta A{)}^{-1}(\exp (\Delta A)-I)\cdot \Delta B\text{\hspace{1em}(1)} \end{gathered}$$

2. 状态空间模型（SSM）的序列到序列转换可以用以下公式表示：

   $$h_t=\overline{A}{h}_{t-1}+\overline{B}{x}_t\text{\hspace{1em}(2)}$$
   $$y_t=C{h}_t\text{\hspace{1em}(3)}$$

其中，t表示当前时刻，表示当前时刻的输入，表示当前时刻的隐藏状态，表示当前时刻的输出。

公式$(2)$的递归特性将类循环神经网络（RNN-like）的状态空间模型与因果注意力机制（Causal attention）区分开，详情见图2。

图 2：从内存角度展示因果注意力机制和类循环神经网络（RNN）模型的机制示意图，其中 $x_i$ 表示第i步的输入令牌。(a) 因果注意力将前面所有令牌的键 $k$ 和值 $v$ 存储为内存。通过不断添加当前令牌的键和值来更新内存，因此这种内存是无损的，但缺点是随着序列变长，整合旧内存和当前令牌的计算复杂度会增加。因此，注意力机制能有效地处理短序列，但在处理长序列时可能会遇到困难。(b) 相比之下，类 RNN 模型将前面的令牌压缩为固定大小的隐藏状态 $h$，以此作为内存。这种固定大小意味着 RNN 的内存本质上是有损的，无法直接与注意力模型的无损内存容量相媲美。尽管如此，类 RNN 模型在处理长序列时可以展现出明显的优势，因为无论序列长度如何，将旧内存与当前输入合并的复杂度保持不变。

3. 隐藏状态 $h$ 可以看作是一个固定大小的内存，用于存储所有历史信息。通过公式$(2)$，这个内存不断更新，同时保持大小不变。固定大小意味着 内存必然存在信息损失 ，但它 确保了将内存与当前输入进行整合的计算复杂度保持不变。
4. 相反，因果注意力 (Causal attention) 将前面所有令牌的键和值存储为其内存，随着新输入的加入，通过添加当前令牌的键和值来扩展内存。这种内存 理论上是无损的。 然而，随着输入令牌的增加，内存大小不断增长，从而增加了将内存与当前输入进行整合的复杂度。
5. 由于 SSM 的内存本质上是有损的，从逻辑上讲，它不如注意力的无损内存。因此，Mamba 在处理短序列时无法展现其优势，而注意力在短序列处理方面表现出色。
6. 在涉及长序列的场景中，注意力由于其二次复杂度会出现性能下降。 在这种情况下，Mamba 在将内存与当前输入进行整合时的效率优势就会凸显出来，从而能够流畅地处理长序列。因此，Mamba 特别适合处理长序列。

图 3：(a) 两种令牌混合模式。对于总共 $T$ 个令牌，全可见模式允许令牌 $t$ 聚合来自所有令牌的输入，即 { x i } i = 1 T \{x_i\}_{i=1}^{T} {xi​}i=1T​，来计算其输出。相比之下，因果模式限制令牌 $t$ 仅聚合来自前面和当前令牌的输入 { x i } i = 1 t \{x_i\}_{i=1}^{t} {xi​}i=1t​。 默认情况下，注意力机制以全可见模式运行，但可以通过因果注意力掩码调整为因果模式。类似 RNN 的模型，如 Mamba 的状态空间模型（SSM），由于其循环特性，本质上以因果模式运行。(b) 我们将视觉 Transformer（ViT）的注意力机制从全可见模式修改为因果模式，并观察到在 ImageNet 上的性能下降，这表明因果混合对于理解任务来说并非必要。

7. 【因果模式】： 状态空间模型（SSM）的递归特性公式 $(2)$ 使Mamba能够高效处理长序列，但它也带来了一个显著的限制制：$h_t$ 只能访问前一个和当前时间步的信息。
   如图3（下图）所示，这种令牌混合方式被称为因果模式，可以用公式表示为：
   $$y_t=f(x_1,x_2,......,x_t)\text{\hspace{1em}(4)}$$

其中，$x_t$ 和 $y_t$ 分别代表第 $t$ 个令牌的输入和输出。由于其因果特性，这种模式非常适合自回归生成任务。

8. 【全可见模式】：在这种模式下，每个令牌都可以聚合来自所有前序和后续令牌的信息。 这意味着每个令牌的输出取决于所有令牌的输入：
   $$y_t=f(x_1,x_2,......,x_T)\text{\hspace{1em}(5)}$$

其中 $T$ 表示令牌的总数。全可见模式适用于理解任务，在这类任务中，模型可以一次性访问所有输入。

Mamba到底适合处理什么样的任务？

Mamba 非常适合具有以下特性的任务：

• 特性 1：任务涉及长序列处理。
• 特性 2：任务需要因果令牌混合模式。

视觉任务具有很长的序列吗？

考虑一个具有常见多层感知机（MLP）比例为 4 的Transformer模块；假设其输入$X\in {\mathbb{R}}^{L\times D}$，那么该模块的浮点运算次数（FLOPs）可以计算为：

$$\text{FLOPs}=24D^{2}L+4D{L}^2$$

由此推导出公式：

$$r_L=\frac{4D{L}^2}{24D^{2}L}=\frac{L}{6D}$$

如果$L>6D$，那么关于$L$的二次项的计算量就会超过一次项的计算量。这提供了一个简单的衡量标准，用于判断该任务是否涉及长序列。

• 例如，在ViT - S模型中有384个通道时，阈值${\tau }_{small}=6\times 384=2304$；而对于ViT - B模型中768个通道的情况，${\tau }_{base}=6\times 768=4608$。

• 对于ImageNet数据集上的图像分类任务，典型的输入图像尺寸为$224\times 224$，当图像块（patch）尺寸为$16\times 16$时，会得到$14\times 14=196$个图像块（令牌）。显然，$196$远小于${\tau }_{small}$和${\tau }_{base}$， 这表明ImageNet上的图像分类任务不能算作长序列任务。

• 对于 COCO 数据集上的目标检测与实例分割任务，推理图像尺寸为$800\times 1280$；对于 ADE20K 数据集上的语义分割任务，推理图像尺寸为$512\times 2048$。当图像块（patch）尺寸为$16\times 16$时，令牌数量大约为$4000$个。

• 由于$4000>{\tau }_{small}=6\times 384=2304$且$4000>{\tau }_{base}=6\times 768=4608$，所以 COCO 数据集上的目标检测任务和 ADE20K 数据集上的语义分割任务都可被视为长序列任务。

如何计算Transformer 模块的浮点运算次数（FLOPs）?

定义

$FLOPs$ 定义：1 次乘法和 1 次加法均计为 1 次 $FLOP$。

一个$D$维行向量与一个$D$维列向量相乘的情况

上图展示了一个$D$维行向量与一个$D$维列向量相乘的情况。
一个$D$维行向量与一个$D$维列向量相乘得到一个结果元素，这需要进行乘法和加法运算，总共的浮点运算次数$（FLOPs）$为$2D$
所以在 这种情况下，1个结果元素需要$2D$次浮点运算。因此$L\times L$个输出元素所需的浮点运算次数是：
$$L\times L\times D=2D{L}^2$$

计算输入

假设输入$X\in {\mathbb{R}}^{L\times D}$，其中$L$表示序列长度（token 数量），$D$表示通道数。查询（queries）、键（keys）和值（values）由
$$Q=X{W}_Q$$
$$K=X{W}_K$$
$$V=X{W}_V$$
计算得到，且计算中涉及的参数$Q,K,V\in {\mathbb{R}}^{L\times D}$以及$W_Q,W_K,W_V\in {\mathbb{R}}^{D\times D}$是可学习的。

计算$Q,K,V$是相似的，我们举其中一个例子。由于一个输出元素需要$2D$次运算，所以$L\times D$输出元素需要$L\times D\times 2D=2D^{2}L$。计算$K$、$V$和计算$Q$类似。

因此总的浮点运算次数是：${\text{FLOP}}_{QKV}=3\times 2D{L}^2=6D^{2}L$。

计算注意力图

$A=Q\times K^T$ ,其中 $A\in {\mathbb{R}}^{L\times L}$ 是注意力图

一个输出元素需要 $2D$ 次浮点运算,因此 $L^2$个输出元素需要 $FLO{P}_A=L^2\times 2D=2D{L}^2$

接下来，使用注意力图对值进行聚合以获得新的值，

$$V^{\prime }=AV$$

其中，$V^{\prime }\in {\mathbb{R}}^{L\times D}$ 是新的值。

一个输出元素需要 $2L$ 次浮点运算$（FLOPS）$，因此 $L\times D$个输出元素需要的浮点运算次数 $$FLO{P}_{V^{\prime }}=L\times D\times 2L=2D{L}^2$$

线性变换

接下来，使用一个线性变换对 $V^{\prime }$ 进行转换，以获得注意力模块的最终输出
$$Y=V^{\prime }{W}_O$$

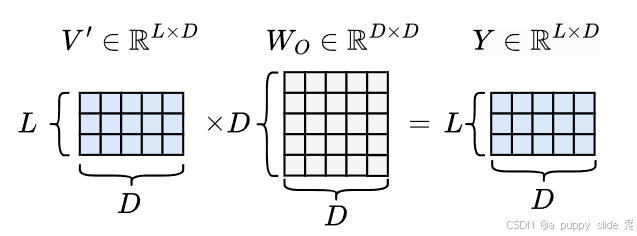
其中，$W_O\in {\mathbb{R}}^{D\times D}$ 是可学习参数，$Y\in {\mathbb{R}}^{L\times D}$ 是注意力模块的输出。

一个输出元素需要$2D$次运算，所以$L\times D$输出元素需要
$$FLOP{s}_Y=L\times D\times 2D=2D^{2}L$$

多层感知机

在注意力模块之后，下一个模块是多层感知机（MLP），其可以表示为：
$$\begin{gathered} Z=\sigma (Y{W}_1) \\ {Z}^{\prime }=Z{W}_2 \end{gathered}$$
其中 $W_1\in {\mathbb{R}}^{D\times 4D}$ 且 $W_2\in {\mathbb{R}}^{4D\times D}$ 是可学习参数，默认的MLP扩展比 $(r)$ 为4。$\sigma (\cdot )$ 是激活函数，其浮点运算次数$（FLOPs）$可忽略不计。

1个输出元素需要 $2D$ 次浮点运算$（FLOPs）$，所以 $L\times 4D$ 个输出元素需要的浮点运算次数（FLOPs）为：
$${\text{FLOP}}_Z=L\times 4D\times 2D=8D^{2}L$$

1个输出元素需要 $8D$ 次浮点运算$（FLOPs）$，所以 $L\times D$ 个输出元素需要的浮点运算次数（FLOPs）为：
$${\text{FLOP}}_{Z^{\prime }}=L\times D\times 8D=8D^{2}L$$

因此，对于一个Transformer模型，总浮点运算次数（FLOPs）为：
$$\begin{gathered} {\text{FLOP}}_{\text{total}}={\text{FLOP}}_{\text{QKV}}+{\text{FLOP}}_1+{\text{FLOP}}_2+{\text{FLOP}}_{V^{\prime }}+{\text{FLOP}}_Z+{\text{FLOP}}_{Z^{\prime }} \\ =6D^{2}L+2D^{2}L+2D^{2}L+2D^{2}L+8D^{2}L+8D^{2}L \\ =24D^{2}L+4D{L}^2 \end{gathered}$$