堆
数据结构入门
堆
是一种满足特定条件的完全二叉树,分为两种类型。
小顶堆
:任意节点的值
≤
其子节点的值。

大顶堆
:任意节点的值
≥
其子节点的值。

常用操作
// 初始化小顶堆
Queue<Integer> minHeap = new PriorityQueue<>();
// 初始化大顶堆(使用 lambda 表达式修改 Comparator 即可)
Queue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b - a);
// 元素入堆
maxHeap.offer(10);
maxHeap.offer(30);
maxHeap.offer(20);
maxHeap.offer(50);
maxHeap.offer(40);
// 获取堆顶元素
int peek = maxHeap.peek(); // 50
System.out.println("大顶堆的堆顶元素: " + peek);
// 堆顶元素出堆
while (!maxHeap.isEmpty()) {
peek = maxHeap.poll(); // 依次出堆元素
System.out.println("出堆元素: " + peek);
}
// 获取堆大小
int size = maxHeap.size();
System.out.println("大顶堆的大小: " + size);
// 判断堆是否为空
boolean isEmpty = maxHeap.isEmpty();
System.out.println("大顶堆是否为空: " + isEmpty);
// 输入列表并建堆
minHeap = new PriorityQueue<>(Arrays.asList(10, 30, 20, 50, 40));
System.out.println("小顶堆中的元素: " + minHeap);
// 输出小顶堆的元素
while (!minHeap.isEmpty()) {
System.out.println("小顶堆出堆元素: " + minHeap.poll());
}- 初始化堆:分别初始化大顶堆和小顶堆。
- 元素入堆:将一些整数值添加到大顶堆中。
- 获取堆顶元素:使用
peek()方法获取堆顶元素。 - 堆顶元素出堆:通过循环使用
poll()方法,逐一取出并显示大顶堆的元素。 - 获取堆大小和是否为空:使用
size()和isEmpty()方法获取相关信息。 - 构建小顶堆:通过输入一个整数列表来填充小顶堆,并显示其元素。
堆的实现
存储与表示
public class BinaryHeap {
// 获取左子节点的索引
public int getLeftChildIndex(int index) {
return 2 * index + 1;
}
// 获取右子节点的索引
public int getRightChildIndex(int index) {
return 2 * index + 2;
}
// 获取父节点的索引
public int getParentIndex(int index) {
return (index - 1) / 2; // 向下取整
}
public static void main(String[] args) {
BinaryHeap heap = new BinaryHeap();
int index = 3; // 示例索引
System.out.println("索引 " + index + " 的左子节点索引: " + heap.getLeftChildIndex(index));
System.out.println("索引 " + index + " 的右子节点索引: " + heap.getRightChildIndex(index));
System.out.println("索引 " + index + " 的父节点索引: " + heap.getParentIndex(index));
}
}
- 左子节点索引:
getLeftChildIndex(int index)方法计算给定索引的左子节点索引。 - 右子节点索引:
getRightChildIndex(int index)方法计算给定索引的右子节点索引。 - 父节点索引:
getParentIndex(int index)方法计算给定索引的父节点索引。
访问堆顶元素
/* 访问堆顶元素 */
int peek() {
return maxHeap.get(0);
}元素入堆
import java.util.ArrayList;
import java.util.List;
public class MaxHeap {
private List<Integer> maxHeap;
public MaxHeap() {
maxHeap = new ArrayList<>();
}
// 元素入堆
public void push(int val) {
// 添加节点
maxHeap.add(val);
// 从底至顶堆化
siftUp(maxHeap.size() - 1);
}
// 从节点 i 开始,从底至顶堆化
private void siftUp(int i) {
while (i > 0) {
// 获取父节点的索引
int p = parent(i);
// 当“越过根节点”或“节点无须修复”时,结束堆化
if (maxHeap.get(i) <= maxHeap.get(p)) {
break;
}
// 交换两节点
swap(i, p);
// 循环向上堆化
i = p;
}
}
// 获取父节点的索引
private int parent(int i) {
return (i - 1) / 2; // 向下整除
}
// 交换节点
private void swap(int i, int j) {
int temp = maxHeap.get(i);
maxHeap.set(i, maxHeap.get(j));
maxHeap.set(j, temp);
}
// 获取堆的大小
public int size() {
return maxHeap.size();
}
public static void main(String[] args) {
MaxHeap heap = new MaxHeap();
heap.push(10);
heap.push(20);
heap.push(15);
heap.push(30);
System.out.println("堆的大小: " + heap.size());
// 可以继续扩展其他堆操作,比如出堆、查看堆顶元素等
}
}
MaxHeap类:实现一个最大堆,其中使用ArrayList存储堆元素。push(int val)方法:用于将元素插入堆中,并调用siftUp方法进行堆化。siftUp(int i)方法:从插入元素的索引向上调整堆,确保最大堆特性得以维持。parent(int i)方法:计算给定节点的父节点的索引。swap(int i, int j)方法:用于交换堆中两个节点的值。size()方法:返回堆的当前大小。
堆顶元素出堆
import java.util.ArrayList;
import java.util.List;
public class MaxHeap {
private List<Integer> maxHeap;
public MaxHeap() {
maxHeap = new ArrayList<>();
}
// 元素入堆
public void push(int val) {
maxHeap.add(val);
siftUp(maxHeap.size() - 1);
}
// 元素出堆
public int pop() {
// 判空处理
if (isEmpty()) {
throw new IndexOutOfBoundsException("堆为空,无法出堆");
}
// 交换根节点与最右叶节点
swap(0, size() - 1);
// 删除节点
int val = maxHeap.remove(size() - 1);
// 从顶至底堆化
siftDown(0);
// 返回堆顶元素
return val;
}
// 从节点 i 开始,从顶至底堆化
private void siftDown(int i) {
while (true) {
// 判断节点 i, l, r 中值最大的节点,记为 ma
int l = left(i), r = right(i), ma = i;
if (l < size() && maxHeap.get(l) > maxHeap.get(ma)) {
ma = l;
}
if (r < size() && maxHeap.get(r) > maxHeap.get(ma)) {
ma = r;
}
// 若节点 i 最大或索引 l, r 越界,则无须继续堆化,跳出
if (ma == i) {
break;
}
// 交换两节点
swap(i, ma);
// 循环向下堆化
i = ma;
}
}
// 获取左子节点的索引
private int left(int i) {
return 2 * i + 1;
}
// 获取右子节点的索引
private int right(int i) {
return 2 * i + 2;
}
// 获取父节点的索引
private int parent(int i) {
return (i - 1) / 2; // 向下整除
}
// 交换节点
private void swap(int i, int j) {
int temp = maxHeap.get(i);
maxHeap.set(i, maxHeap.get(j));
maxHeap.set(j, temp);
}
// 获取堆的大小
public int size() {
return maxHeap.size();
}
// 判空
public boolean isEmpty() {
return maxHeap.isEmpty();
}
public static void main(String[] args) {
MaxHeap heap = new MaxHeap();
heap.push(10);
heap.push(20);
heap.push(15);
heap.push(30);
System.out.println("出堆元素: " + heap.pop()); // 应该是30
System.out.println("堆的大小: " + heap.size());
// 继续测试其他出堆操作
}
}
MaxHeap类:实现一个最大堆,使用ArrayList存储堆元素。push(int val)方法:用于将元素插入堆,并调用siftUp方法进行堆化。pop()方法:弹出堆顶元素,过程中会交换堆顶和堆末尾元素,移除堆末尾元素,并调用siftDown方法进行堆化。siftDown(int i)方法:从给定节点开始向下调整堆,确保最大堆特性得以维持。- 辅助方法:
left(int i)和right(int i)方法用于获取左子节点和右子节点的索引。parent(int i)方法计算给定节点的父节点的索引。swap(int i, int j)方法用于交换堆中两个节点的值。size()方法返回堆的当前大小。isEmpty()方法检查堆是否为空。
建堆操作
借助入堆操作
先创建一个空堆,然后遍历列表,依次对每个元素执行“入堆操作”
遍历堆化
import java.util.ArrayList;
import java.util.List;
public class MaxHeap {
private List<Integer> maxHeap;
// 构造方法,根据输入列表建堆
public MaxHeap(List<Integer> nums) {
maxHeap = new ArrayList<>(nums);
for (int i = (maxHeap.size() - 2) / 2; i >= 0; i--) {
siftDown(i);
}
}
private void siftDown(int i) {
// 堆化过程略
}
public static void main(String[] args) {
List<Integer> nums = List.of(10, 20, 15, 30);
MaxHeap heap = new MaxHeap(nums);
// 可以添加其他测试代码
}
}
- 构造方法:接收一个整数列表,将其复制到
maxHeap,并从最后一个非叶节点开始堆化。 - siftDown 方法:负责从特定节点开始向下调整堆。
Top‑k 问题
给定一个长度为 𝑛 的无序数组 nums ,请返回数组中最大的 𝑘 个元素。
遍历
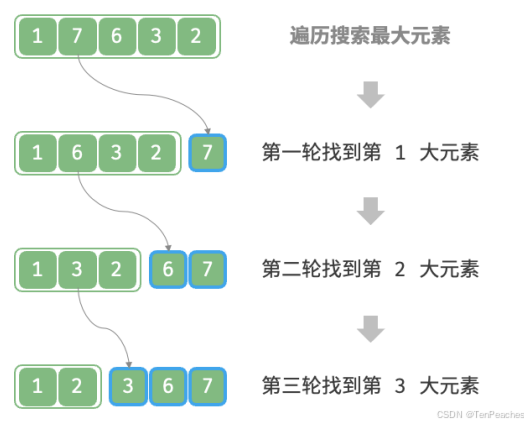
排序

堆
- 初始化一个小顶堆(优先级队列)。
- 将数组前 k 个元素放入堆中作为初始堆。
- 遍历数组从第 k + 1 个元素开始,检查每个元素是否大于堆顶元素:若是,则出堆堆顶元素并入堆当前元素。
import java.util.PriorityQueue;
import java.util.Queue;
public class TopKElements {
// 基于堆查找数组中最大的 k 个元素
public Queue<Integer> topKHeap(int[] nums, int k) {
// 初始化小顶堆
Queue<Integer> heap = new PriorityQueue<>();
// 将数组的前 k 个元素入堆
for (int i = 0; i < k; i++) {
heap.offer(nums[i]);
}
// 从第 k+1 个元素开始,保持堆的长度为 k
for (int i = k; i < nums.length; i++) {
// 若当前元素大于堆顶元素,则将堆顶元素出堆、当前元素入堆
if (nums[i] > heap.peek()) {
heap.poll();
heap.offer(nums[i]);
}
}
return heap;
}
public static void main(String[] args) {
TopKElements topK = new TopKElements();
int[] nums = {3, 1, 5, 12, 2, 11};
int k = 3;
Queue<Integer> result = topK.topKHeap(nums, k);
System.out.println("最大的 " + k + " 个元素: " + result);
}
}
重点知识
堆排序
构建堆:将待排序序列构建成一个堆。
排序:重复从堆中取出最大/最小元素,然后重新调整堆,直到堆为空。
import java.util.Arrays;
public class HeapSort {
// 堆化过程:从节点 i 开始,向下调整堆
private void heapify(int[] arr, int n, int i) {
int largest = i; // 初始化最大元素为根节点
int left = 2 * i + 1; // 左子节点的索引
int right = 2 * i + 2; // 右子节点的索引
// 如果左子节点比根节点大
if (left < n && arr[left] > arr[largest]) {
largest = left;
}
// 如果右子节点比当前最大元素大
if (right < n && arr[right] > arr[largest]) {
largest = right;
}
// 如果最大元素不是根节点,交换并继续堆化
if (largest != i) {
swap(arr, i, largest);
heapify(arr, n, largest);
}
}
// 交换数组中两个元素的位置
private void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
// 主堆排序方法
public void sort(int[] arr) {
int n = arr.length;
// 建立最大堆
for (int i = n / 2 - 1; i >= 0; i--) {
heapify(arr, n, i);
}
// 一个个从堆中取出元素
for (int i = n - 1; i > 0; i--) {
swap(arr, 0, i); // 将当前根节点(最大值)移动到数组的末尾
heapify(arr, i, 0); // 重新调整堆
}
}
public static void main(String[] args) {
HeapSort heapSort = new HeapSort();
int[] arr = {12, 11, 13, 5, 6, 7};
System.out.println("原数组: " + Arrays.toString(arr));
heapSort.sort(arr);
System.out.println("排序后数组: " + Arrays.toString(arr));
}
}
heapify方法:用于从给定节点开始,向下调整堆。确保以该节点为根的子树满足最大堆的性质。swap方法:用于交换数组中两个元素的位置。sort方法:主堆排序方法。- 首先通过
heapify方法建立最大堆。 - 然后从堆中提取元素,交换根节点与最后一个节点,并再次对堆进行调整。
- 首先通过
文章记录了学习Krahets的《Hello 算法》的轨迹,代码均使用Java语言,原书支持 Python、C++、Java、C#、Go、Swift、JavaScript、TypeScript、Dart、 Rust、C 和 Zig 等语言。
























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








