单向队列的动态模拟实现-优快云博客

本文链接：https://blog.youkuaiyun.com/2402_88062890/article/details/146996829

1.单向队列的定义

2.单向队列的底层逻辑

1.单向队列的定义

日常生活中我们随处可见人们排队参加某项活动的场景，在道德的约束下排队的原则是先排的先完成该项活动。这种规则与数据结构里面的单向队列十分相似。

单向队列遵循着先进先出的规则。

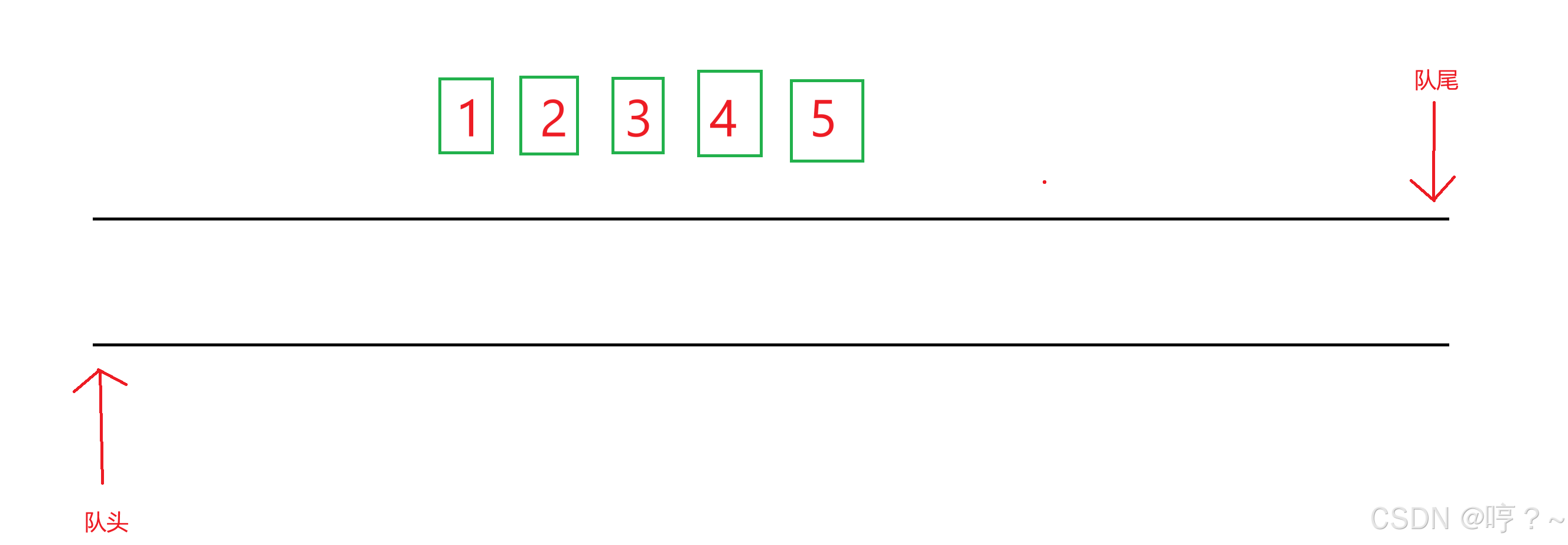
在单向队列中，由于受到先进先出的影响，元素只能在队尾进行入队操作，只能在对头进行出队操作

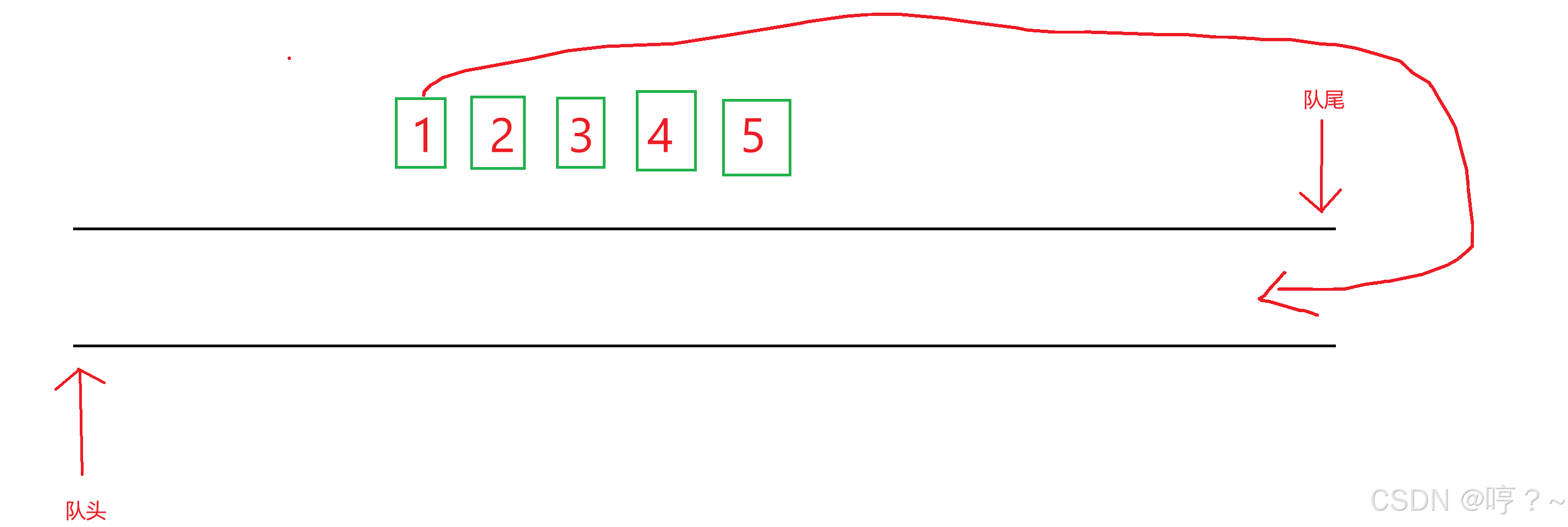
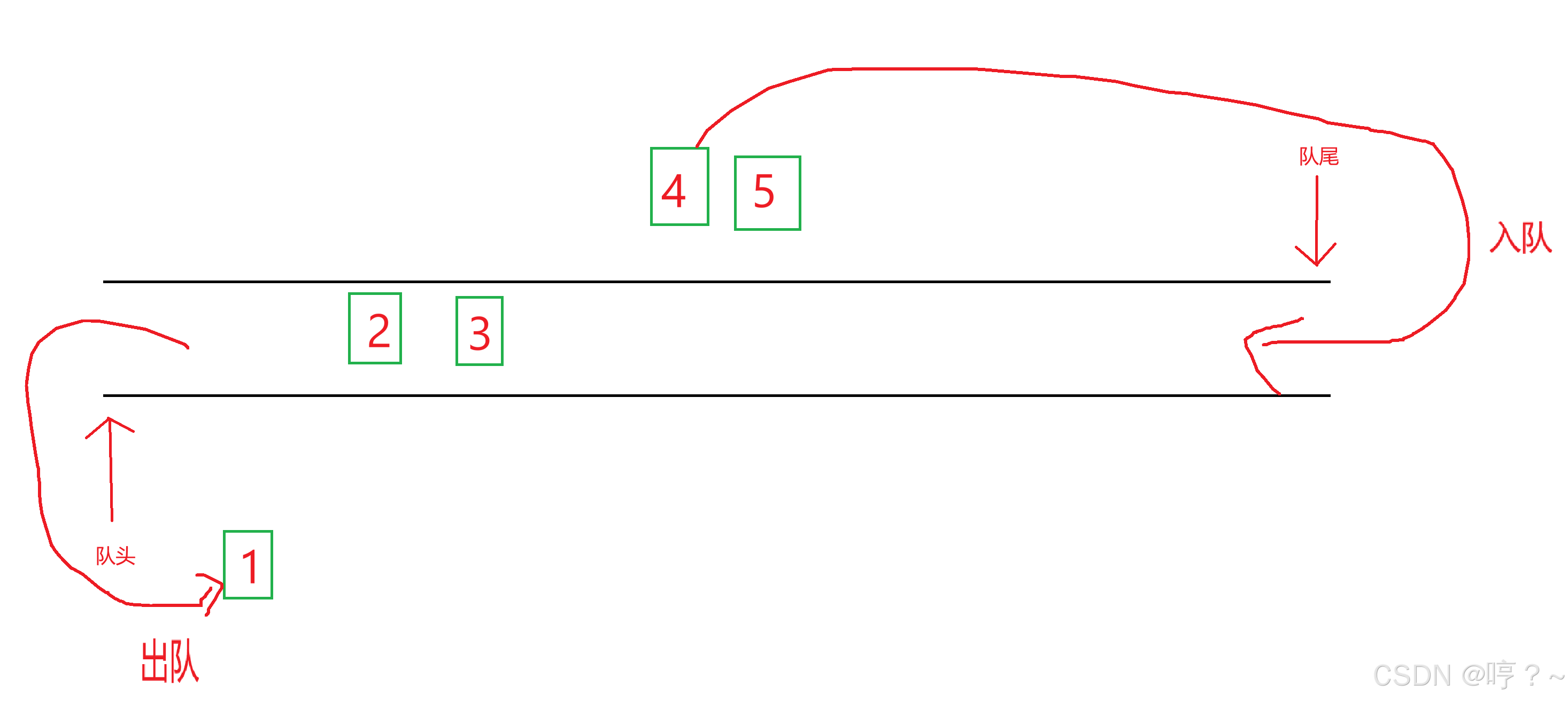
2.单向队列的底层逻辑

实际上无论是用数组还是链表都能实现队列，但是链表能够更好的体现队列中元素的相关性以及更加方便的进行队列的尾部处理。

3.单向队列的模拟实现

队列的创建同样需要借助结构体，在结构体中需要存储当下节点存储的数据、能够找到前驱以及后继节点的结构体指针、如果有需要的话再加上队列的元素数量。

typedef int Data_type;
typedef struct queue
{
	Data_type data;
	struct queue* phead;//后继指针
	struct queue* ptail;//前驱指针
	int size;
}QE;

1.创建与初始化

在将要实现插入操作时，我们都需要提前给插入数据开辟空间，为了使代码更加简洁易读，我们额外分装一个函数用于创建新节点。

QE* queue_create(QE* ps, Data_type x)
{
    assert(ps);
    QE* mid = (QE*)malloc(sizeof(QE));
    assert(mid);
    mid->data = x;
    mid->phead = mid->ptail = NULL;  // 新节点初始时前后指针都为 NULL
    return mid;
}

在queue_create函数里，我们使用malloc开辟空间，当开辟空间成功后初始化结构体里元素。

2.插入与删除

插入

对于单向链表而言，插入只能是尾插。

如果需要遍历来寻找队列尾部节点的话，时间复杂度将为O（N），效率并不高。这时，我们借助双向链表的思路，将头节点的前驱指针指向尾节点便可以以O（1）的复杂度完成插入操作。

在插入过程中，我们需要更新头节点的前驱指针，原尾节点的后继指针以及新节点的前驱指针。以及队列元素数量的自加。

void queue_push(QE* ps, Data_type x)
{
    assert(ps);
    QE* mid = queue_create(ps, x);//为新数据开辟空间
    assert(mid);
    //当队列为空时
    if (ps->size == 0)
    {
        ps->phead = ps->ptail = mid;
    }
    else
    {
        ps->ptail->ptail = mid;
        mid->phead = ps->ptail;
        ps->ptail = mid;
    }
    ps->size++;
}

删除

单向队列的删除只能是头删

删除过程需要删除原头节点（记得销毁），使原头节点的后继成为新头节点并更改其前驱指针。以及队列元素数量的自减。

void queue_pop(QE* ps)
{
    assert(ps);
    if (ps->size > 0) 
    {
       //这里作者的ps为队列的哨兵位，
       //在一般情况下可以不用额外设立哨兵
        QE* temp = ps->phead;
        if (ps->size == 1) 
        {
            ps->phead = ps->ptail = NULL;
        }
        else 
        {
            ps->phead = ps->phead->ptail;
            ps->phead->phead = NULL;
        }
        free(temp);
        temp=NULL;
        ps->size--;
    }
}

3.队列判空与获取队列有效元素个数

判空

判空操作使用布尔类型的函数，直接返回队列是否为空

bool queue_empty(QE* ps)
{
    assert(ps);
    return ps->size == 0;
}

获取有效元素个数

直接返回size即可

int queue_size(QE* ps)
{
    assert(ps);
    return ps->size;
}

4.获取队列顶元素

由于我们创建的队列头节点的前驱指针可以找到尾节点，便一切好说。

Data_type queue_top(QE* ps)
{
    assert(ps);
    assert(!queue_empty(ps));
    return ps->phead->data;
}

5.销毁

销毁我们可以调用删除函数，循环执行删除操作直到队列为空

void queue_destroy(QE* ps)
{
    assert(ps);
    while (!queue_empty(ps)) {
        queue_pop(ps);
    }
}