数据结构概述
数据结构指的是计算机存储数据和组织数据的方式,存储数据和组织数据的目的是为了后期对数据的再次利用,所以存储的数据一般是具有一个或者多个特定关系的集合,利用不同的数据结构可以提高数据的访问效率。
思考:为什么大家来到新教室选好座位之后需要填写座位表?? 答案:方便管理班级学生
数据指的是可以被输入到计算机并且可以被计算机处理的符号的总称,数据的英文是Data。
数据是有单位的,数据的基本单位是数据元素(Data Element),在计算机中数据元素是作为整体来处理的,比如学生的信息。数据元素是由多个数据项组成的,所以数据项也被称为数据的最小单位,比如学生信息中的学号、姓名、年龄,数据项属于数据元素不可分割的一部分。
举例:比如国家是数据元素,则每个国家的城市就是数据项,数据项是数据不可分割的部分。
注意:世界上不止有一个国家,如果每个国家都是数据元素的话,则多个数据元素的集合就被称为数据对象(Data Object)。
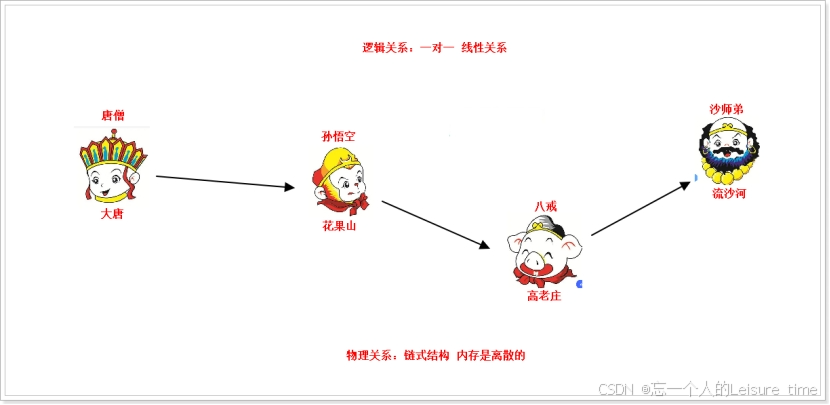
数据结构就是描述多个数据之间的逻辑结构和物理结构。逻辑结构指的是数据元素之间的逻辑关系,物理结构指的是计算机中存储数据的方式,所以物理结构也被称为存储结构。
注意:数据元素的逻辑关系和物理关系没有必然的联系,数据元素可能同时存储逻辑关系和物理关系,数据元素之间也可能只存在一种关系,或者数据元素之间一种关系都没有。
对于数据结构的逻辑关系,可以分为四种:集合(无关系)、线性结构(一对一)、树状结构(一对多)、图状结构(多对多)。
数据的物理关系可以分为两种:一种是顺序结构(连续存储),另一种是离散结构(离散存储),一般把顺序结构也称为顺序存储,一般把离散结构也称为链式存储,两种区别如下图
逻辑上(线性结构、非线性结构)
物理上(顺序结构、链式结构)
广义上讲算法是研究数据之间的逻辑关系 ,然后选择某种方案来存储数据,并在此基础上对数据进行处理,其实更加直白的说:算法指的是计算或者解决问题的步骤。
请问:如果把下面的一个随机数列中的数值按照从小到大顺序进行排列??具体步骤是什么??
有穷性:指的是程序执行必须在有限次数内完成,而每一次必须在有限时间内执行完成。
确定性:执行的每一条语句都必须有准确的解释,不能出现二义性,意味着相同的输入 就会相同的输出。
可行性:程序中每一条复杂语句都可以分解为基本指令,并且每条基本指令都必须在有 限时间完成。
输入项:指的是算法可以有一个或者多个参数作为初始条件,然后对程序进行有效执行。
输出项:指的是算法经过运算之后可以有一个或者多个输出,所以一个有意义的算法是 应该有输出结果的。
总结:一个程序的执行是需要用户选择合适的算法和数据结构的,
程序 = 数据结构+算法。
思考:到底什么样的数据结构和算法是合适的?怎么去评定选择的数据结构和算法是否合适?
回答;对于数据结构的选择和算法的选择并不是唯一的,但是选择要是合适的,衡量数据结构和算法的选择是否合适,取决于算法实现的运行时间和内存空间。一般是通过两个专业性名称,分别是“时间复杂度”和“空间复杂度”。
时间复杂度不是算法的运行时间来衡量,因为程序的运行时间取决于CPU的性能,不同性能的CPU执行指令的周期是不一样的,比如8bit单片机的主频是12MHZ,而32bit单片机的主机可以168MHZ,而计算机的CPU主频都是xxx.GHZ 。
时间复杂度指的是算法程序的语句的执行次数,也可以称为语句频度,一个程序的语句执行次数越多,则时间复杂度越大,则说明算法不合适。时间复杂度一般采用数学符号大O()表示,一般时间复杂度的计算中都会出现n,n表示规模,对于时间复杂度是表示算法的趋势。
一般会把算法程序的语句的执行次数用T()表示,但是对于函数T()可能是一个多项式,而时间复杂度就是找出函数T()影响最大的项,所以时间复杂度是执行语句的估算值,使用数学符号大O()表示。O其实是order的缩写。大O的括号中写的值就是影响程序执行语句最大的那个项。
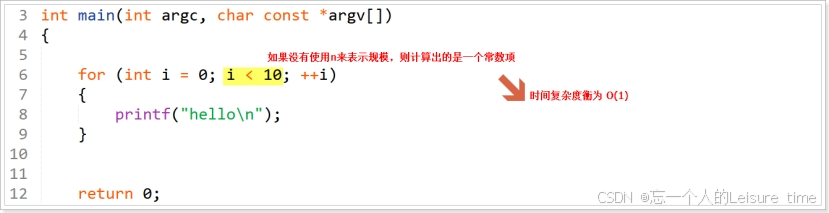
计算技巧:只需要计算出算法的基本执行语句的最高次项,并且把最高次项的系数舍弃,就是算法的时间复杂度,需要使用数学符号O(xxx),如果计算出的是常数项,则时间复杂度衡为O(1)。
空间复杂度指的是程序运行期间所需要的内存空间,空间复杂度越大,则说明程序运行期间需要的内存越多,则说明算法不合适。
注意:程序中的时间复杂度和空间复杂度是可以互相转换的,一般情况下是相互制约的,意味着“鱼和熊掌不可兼得”,所以用户根据实际情况去选择时间还是空间,意味着要选择合适的算法来保持平衡。
一个好的算法通常是执行时间短,占用空间少,并且可读性好、容易维护,易于移植到其他平台。
B
大家在学习C语言的时候接触的数组在数据结构中是属于线性表的一种,线性表是由一组具有n个相同类型的数据元素组成的。
线性表中的任何一个数据元素有且只有一个
直接前驱,以及有且只有一个
直接后继,另外首元素是没有前驱的,尾元素是没有后继的。
某个元素的左侧相邻元素被称为“直接前驱”,元素左侧所有的数据元素被称为“前驱元素”。
某个元素的右侧相邻元素被称为“直接后继”,元素右侧所有的数据元素被称为“后继元素”。
满足这种数学关系的一组元素,逻辑关系就是线性结构,并且逻辑关系是一对一的,比如一个教室学生的学号、一个排队的队伍、一摞堆好的盘子.....都属于线性结构,当然线性结构和存储方式是无关的,简单理解:只有逻辑关系是一对一的,就是线性结构。
所以,根据数据的存储方式可以把线性表分为两种:顺序存储的线性表,链式存储的线性表。
顺序表指的是使用一组内存地址连续的内存单元来依次存储线性表中的数据元素,使用这种存储结构的线性表就被称为顺序表。
简单理解:数据存储在一块连续的内存中,在C语言中可以具名的数组,也可以使用匿名的数组(堆内存)。
顺序表的特点:数据元素之间的逻辑关系是相邻的,并且内存地址也是相邻的,所以只要知道存储线性表的第一个数据元素的内存地址,就可以对线性表中的任意一个元素进行随机访问。通常用户使用动态分配的数组来实现顺序表,也就是使用堆内存实现。
随机访问指的是在同等时间内具有访问任意元素的能力,和随机访问相对立的就是顺序访问,顺序访问花费的时间要高于随机访问,比如卷轴(顺序)和书籍(随机)、磁带(顺序)和唱片(随机)。
练习:请问该笔试题的结果是什么?请给出简单的推理过程,请独立完成该笔试题的分析。
A
练习:请问该笔试题的结果是什么?请给出简单的推理过程,请独立完成该笔试题的分析。
B:线性表采用顺序存储时,插入和删除操作往往需要移动大量元素,因为要保持元素的连续性,所以并不便于进行插入和删除操作,该选项错误。
练习:请问该笔试题的结果是什C么?请给出简单的推理过程,请独立完成该笔试题的分析。
C: 在顺序表中插入一个元素时,若要在第 i 个位置插入新元素,需要将第 i 到第 n(n 为顺序表当前长度)个元素依次向后移动一位,平均情况下移动元素的次数为 n/2,时间复杂度为 O (n)
思考:既然数组可以作为线性表来使用,请问如何对数组中的元素进行增加和删除以及访问?
回答:如果打算使用数组实现线性表的特性,需要知道三个条件:
数组首元素地址、数组元素的容量、数组有效的最后一个元素的下标。
笔试题:
笔试题:
链表的原理与应用
大家可以知道对于顺序表的数据增加和删除是比较麻烦,因为都需要移动一片连续的内存。
顺序表的优点是:由于顺序表数据元素的内存地址都是连续的,所以可以实现随机访问,而且不需要多余的信息来描述相关的数据,所以存储密度高。
顺序表的缺点是:顺序表的数据在进行增删的时候,需要移动成片的内存,另外,当数据元素的数量较多的时候,需要申请一块较大的连续的内存,同时当数据元素的数量的改变比较剧烈,顺序表不灵活。
思考:既然顺序表实现数据的增加和删除比较麻烦,又占用连续内存,请问有没有更好方案?
回答:是有的,可以利用
链式存储的线性表实现,链式存储指的是采用离散的内存单元来存储数据元素,用户需要使用某种方式把所有的数据元素连接起来,这样就可以变为链式线性表,简称为链表,链表可以高效的使用碎片化内存。
可以看到,顺序表和链式表的区别:顺序表使用连续的内存,链式表使用离散的内存空间。
思考:既然链表中的每个数据元素的地址都是不固定的,请问用户如何访问某个元素呢???
回答:由于链表中的每个数据元素的地址是不固定的,所以每个数据元素都应该使用一个指针指向直接后继的内存地址,当然最后一个数据元素没有直接后继,所以最后一个数据元素指向NULL即可,作为用户只需要知道第一个数据元素的内存地址,就可以访问后继元素了。
注意:如果采用链式存储,则线性表中每一个数据元素除了存储自身数据之外,还需要额外存储直接后继的地址,所以链表中的每一个数据元素都是由
两部分组成:存储自身数据的部分被称为
数据域,存储直接后继地址的部分被称为
指针域,数据域和指针域组成的数据元素被称为
结点(Node)。
注意:链表的工作原理其实很简单,只要大家搞清楚链表的使用流程就可以很轻松的理解,链表具体的操作步骤如下所示:
根据链表的结点的指针域的数量以及根据链表的首尾是否相连,把链式线性表分为以下几种:
单向链表、单向循环链表、双向链表、双向循环链表、内核链表。这几种链表的使用规则差不多,只不过指针域数量不同。
上图就是最简单的
单向链表的内部结构,可以看到每一个结点都保存了一个地址,每个地址都是逻辑上相邻的下一个结点的地址,只不过末尾结点的指针指向NULL。
另外注意:可以看到链表中是有一个头指针的,
头指针只指向第一个元素的地址,想要访问链表中的某个元素只需要通过头指针即可。
思考:使用顺序表的时候需要创建一个管理结构体来管理顺序表,请问链表需不需要创建???
回答:可以根据用户的需要来选择,一般把链表分为两种:一种是不带头结点的链表,一种是带头结点的链表,
头结点指的是管理结构体,只不过头结点只存储第一个元素的内存地址,头结点并不存储有效数据,头结点的意义只是为了方便管理链表。
不带头结点的链表
附带头结点的链表
可以知道,头指针是必须的,因为通过头指针才可以访问链表的元素,
头结点是可选的,只是为了方便管理链表而已。
注意:在链表中,还有两个专业名称,一个是首结点,一个是尾结点,三者之前的区别如下:
头结点:是不存储有效数据的,只存储第一个数据元素的地址,头指针只指向头结点。
首结点:是存储有效数据的,也存储直接后继的内存地址,首结点就是第一个结点,首 结点是唯一一个只指向别的结点,不被别的结点指向的结点。
尾结点:是存储有效数据的,尾结点就是链表的最后一个结点,所以尾结点中存储的地 址一般指向NULL,尾结点是唯一一个只被别的结点指向,不能指向别的结点 的结点。
为了方便管理单向链表,所以需要构造头结点的数据类型以及构造有效结点的数据类型,如下:
创建一个空链表,由于是使用头结点,所以就需要申请头结点的堆内存并初始化即可。
创建一个新结点,并为新结点申请堆内存以及对新结点的数据域和指针域进行初始化。
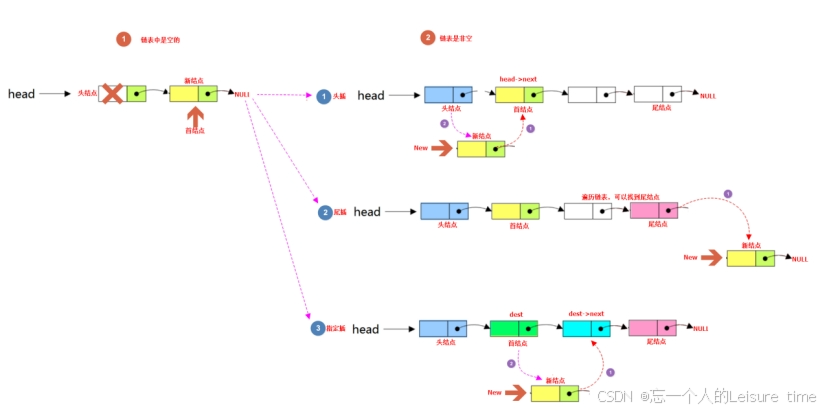
根据情况把新结点插入到链表中,此时可以分为尾部插入、头部插入、指定位置插入。
根据情况可以从链表中删除某结点,此时可以分为尾部删除、头部删除、指定元素删除。
笔试题:
B
笔试题:
D
笔试题:
B
笔试题:
笔试题:
单向循环链表的原理与应用
思考:对于单向链表而言,想要遍历链表,则必须从链表的首结点开始进行遍历,请问有没有更简单的方案实现链表中的数据的增删改查?
回答:是有的,可以使用单向循环的链表进行设计,单向循环的链表的使用规则和普通的单向链表没有较大的区别,需要注意:
单向循环链表的尾结点的指针域中必须指向链表的首结点的地址,由于带头结点的单向循环链表更加容易进行管理,所以教学以带头结点的为例:
上图所示的就是一个典型的单向循环链表的结构,可以发现单向循环链表的结构属于环形结构,链表中的最后一个结点的指针域中存储的是链表的第一个结点的地址。
为了管理单向循环链表,需要构造头结点的数据类型以及构造有效结点的数据类型,如下:
创建一个空链表,由于是使用头结点,所以就需要申请头结点的堆内存并初始化即可!
创建新结点,为新结点申请堆内存并对新结点的数据域和指针域进行初始化,操作如下:
根据情况把新结点插入到链表中,此时可以分为尾部插入、头部插入、指定位置插入:
根据情况可以从链表中删除某结点,此时可以分为尾部删除、头部删除、指定元素删除:
双向链表的原理与应用
如果想要提高单向链表或者单向循环链表的访问速度,则可以在链表中的结点中再添加一个指针域,让新添加的指针域指向当前结点的直接前驱的地址,也就意味着一个结点中有两个指针域(prev + next),也被称为双向链表(Double Linked List)。
由于带头结点更加方便用户进行数据访问,所以本次创建一条带头结点的双向不循环的链表。
创建一个空链表,由于是使用头结点,所以就需要申请头结点的堆内存并初始化即可!
创建新结点,为新结点申请堆内存并对新结点的数据域和指针域进行初始化,操作如下:
根据情况可以从链表中插入新结点,此时可以分为尾部插入、头部插入、指定位置插入:
根据情况可以从链表中删除某结点,此时可以分为尾部删除、头部删除、指定结点删除:
双向循环链表的原理与应用
双向循环链表与双向链表的区别:指的是双向循环链表的首结点中的prev指针成员指向链表的尾结点,并且双向循环链表的尾结点里的next指针成员指向链表的首结点,所以双向循环链表也属于环形结构。
由于带头结点更加方便用户进行数据访问,所以本次创建一条带头结点的双向循环的链表。
创建一个空链表,由于是使用头结点,所以就需要申请头结点的堆内存并初始化即可!
创建新结点,为新结点申请堆内存并对新结点的数据域和指针域进行初始化,操作如下:
根据情况可以从链表中插入新结点,此时可以分为尾部插入、头部插入、指定位置插入:
根据情况可以从链表中删除某结点,此时可以分为尾部删除、头部删除、指定结点删除:
练习:
D
练习:
B
练习:
D
练习:
A
练习:
A
练习:
D
练习:
A
练习:
B




































































































 2891
2891

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








