链式结构的二叉树

最新推荐文章于 2025-06-11 22:39:42 发布

脆皮炸鸡226

最新推荐文章于 2025-06-11 22:39:42 发布

阅读量1.1k

点赞数 36

分类专栏：数据结构文章标签：经验分享学习方法数据结构程序人生笔记

本文链接：https://blog.youkuaiyun.com/2402_83250773/article/details/146570075

版权

这个链式结构同时适用于不完全二叉树。

在这里插入图片描述
在一个结点中，存储着三个内容，这个结点的值+左孩子结点+右孩子结点。

文章目录

一、二叉树的创建
二、二叉树的遍历

一、二叉树的创建

我们可以给（创建新结点）封装成一个函数，每次使用时调用即可。

在此之前，先写出二叉树每个结点的结构体：

typedef int BTDatatype;
//结点的结构体
typedef struct binaryTreeNode
{
   
	BTDatatype data;               //存储的数据
	struct binaryTreeNode* left;   //指向左子树的指针
	struct binatyTreeNode* right;  //指向右子树的指针
}BTNode;


//创建新结点
BTNode* BuyNode(BTDatatype x)
{
   
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	if (newnode == NULL)
	{
   
		perror("malloc fail!");
		exit(1);
	}
	//到这里则代表新结点不为空
	newnode->data = x;
	newnode->left = newnode->right = NULL;
	return newnode;
}

记得在写完代码之后进行测试：

在这里插入图片描述

二、二叉树的遍历

共有三种遍历方式

二叉树三种遍历的介绍

前序遍历

顾名思义：从前往后。（正常看一棵树，肯定是先看根节点，然后看左右结点。前序遍历便是如此）同时，前序遍历也叫做先序遍历，先根遍历。

前序遍历：访问根节点在遍历左右子树之前。
---------------先访问根节点，再左子树，再右子树。

还需要注意的是：在访问根节点之后去访问左子树，

练习：写出这棵二叉树的遍历顺序
在这里插入图片描述
将二叉树分为根，左子树，右子树后，再分别将左右子树均看成一棵树，再分，直到遇到空指针就可以停下了

最先开始，我们处于根：在1这里

接下来找根的左子树：即来到2这棵二叉树（在2这棵二叉树中，根节点是2，同时也要遵循“根左右”，去找根(2)的左子树）

接下来是2的左：即4这棵二叉树（在4这棵二叉树中,根节点是4,也要遵循“根左右”，接下来找根(4)的左子树）

接下来是4的左：即空。这个时候无法再继续进行拆分，因此，递归结束，返回(特定的值)，到这里，就说明我们将以1为根的这棵子树的左子树全部都访问完了。且返回到了那个空的根(即4)，去找这个根的右子树（在4这棵二叉树中，我们已经访问了根节点4和左孩子空，接下来该访问4的右子树：即6）

6这棵二叉树，根结点是6，接下来左NULL，无法拆分，这层递归结束。紧接着返回上一级：6。接着右子树：NULL。到此：6这棵二叉树已经访问完毕了。

在一棵二叉树访问完毕之后(根左右)，此时这在这棵数的右子树处，我们需要回到根结点。这个根结点如果是某棵树的左孩子，那么接下来访问这棵树的右孩子。如果是某棵树的右孩子，那么接下来回这棵树的根结点。

在这里插入图片描述

按照上面说的方法：1，2，4，6，5，3

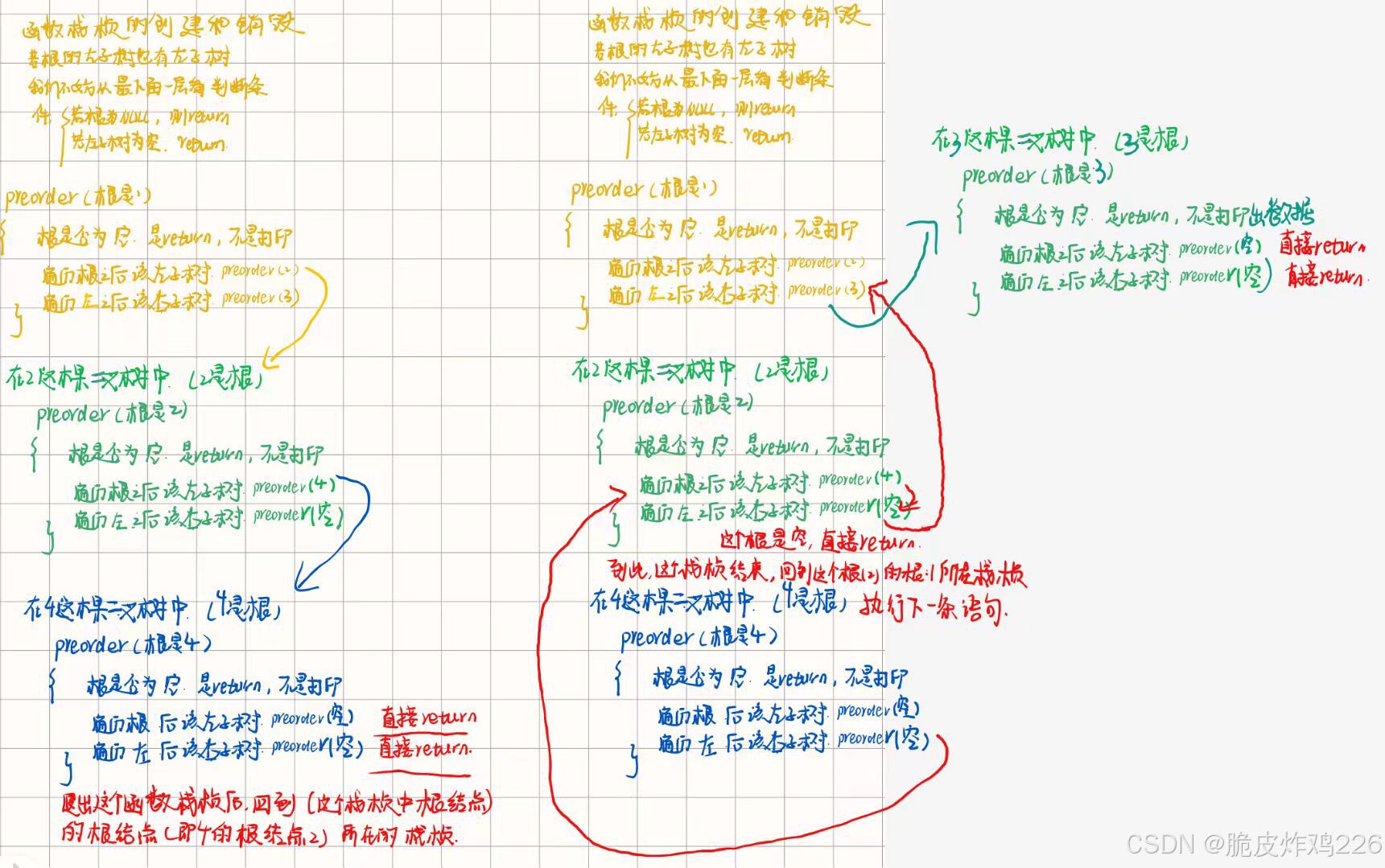
这个遍历过程是一层套一层，要完成这个过程靠的是递归的思想，当我们遇到空指针的时候，就会返回到上一个递归这个函数的位置，进行下一条语句。

中序遍历

中序：访问根节点在遍历左右子树中间。（先左，再根，再右）

在这里插入图片描述

我们现在在1这棵二叉树中，先左，我们需要去左子树，即2这棵二叉树。但是2这棵树又有自己的左子树。那要不要先打印2呢？先不着急打印。先来到2这棵二叉树的左子树：即4这棵数。但4这棵二叉树的左子树是空，所以接下来是根，即4；接下来右，即6。至此位置，4这棵二叉树已经打印完毕。

而4又是2那棵二叉树的左子树(已经遍历完毕了)，接下来是根，即2，接下来右，即5。至此为止，2这棵二叉树已经遍历完毕，接下来是根，即1.接下来右，即3.

所以是4，6，2，5，1，3
在这里插入图片描述

后序遍历

后序：访问根节点在左右子树之后。（左，右，根）

后序和中序很像，都是要先一直往后走，找到左。

最开始指向根，根的左子树又有自己的左子树，我们要找到一个子树，它的左子树为NULL，这个时候我们才能去找其他的
在这里插入图片描述

我们现在在1这棵二叉树中（根结点是1），先左–>我们需要去左子树，即2这棵二叉树。但是2这棵树又有自己的左子树。那要不要先打印2呢？先不着急打印。（我们需要找它的左）先来到2这棵二叉树的左子树：即4这棵数。但4这棵二叉树的左子树是空，所以接下来是右，即6；接下来根，即4。至此位置，4这棵二叉树已经打印完毕。

而4又在2这棵二叉树中，是它的左子树，接下来找右子树，即5，接下来根，即2。至此位置，2这棵二叉树已经打印完毕。

而2又处于1这棵二叉树的左子树的位置，接下来是1这棵树的右子树3，接下来根1.

所以是：6，4，5，2，3，1

二叉树的实现

前序的实现

函数的参数：将二叉树的根结点传过去。（将它的地址传过去）

void BTPreOrder(BTNode* root)
{
   
	if (root == NULL)
	{
   
		return;
	}
	//我们这个是遍历，可以将根先打印出来
	printf("%d ", root->data);
	//如果根结点不为空，先找它的左子树，再找右子树
	BTPreOrder(root->left)