ShuffleNet：通道的打乱与混洗

最新推荐文章于 2025-03-27 20:32:27 发布

2401_89791727

最新推荐文章于 2025-03-27 20:32:27 发布

阅读量1k

点赞数 8

文章标签：深度学习机器学习人工智能

本文链接：https://blog.youkuaiyun.com/2401_89791727/article/details/145097826

版权

背景：

===

为了降低计算量，当前先进的卷积网络通常在3×3卷积之前增加一个1×1卷积，用于通道间的信息流通与降维。然而在ResNeXt、MobileNet等高性能的网络中，1×1卷积却占用了大量的计算资源。 2017年的ShuffleNet v1从优化网络结构的角度出发，利用组卷积与通道混洗（Channel Shuffle）的操作有效降低了1×1逐点卷积的计算量，是一个极为高效的轻量化网络。而2018年的ShuffleNet v2则在ShuffleNet v1版本的基础上实现了更为优越的性能，本节将详细介绍这两个ShuffleNet网络的思想与结构。

通道混洗简述

当前先进的轻量化网络大都使用深度可分离卷积或者组卷积，以降低网络的计算量，但这两种操作**都无法改变特征的通道数，因此还需要使用1×1卷积。**总体来讲，逐点的1×1卷积有如下两点特性：

可以促进通道之间信息的融合，改变通道至指定维度。
轻量化网络中1×1卷积占据了大量的计算，并且致使通道之间充满约束，一定程度上降低了模型的精度。为了进一步降低计算量，ShuffleNet提出了通道混洗的操作，通过通道混洗也可以完成通道之间信息的融合，具体结构如下图所示。

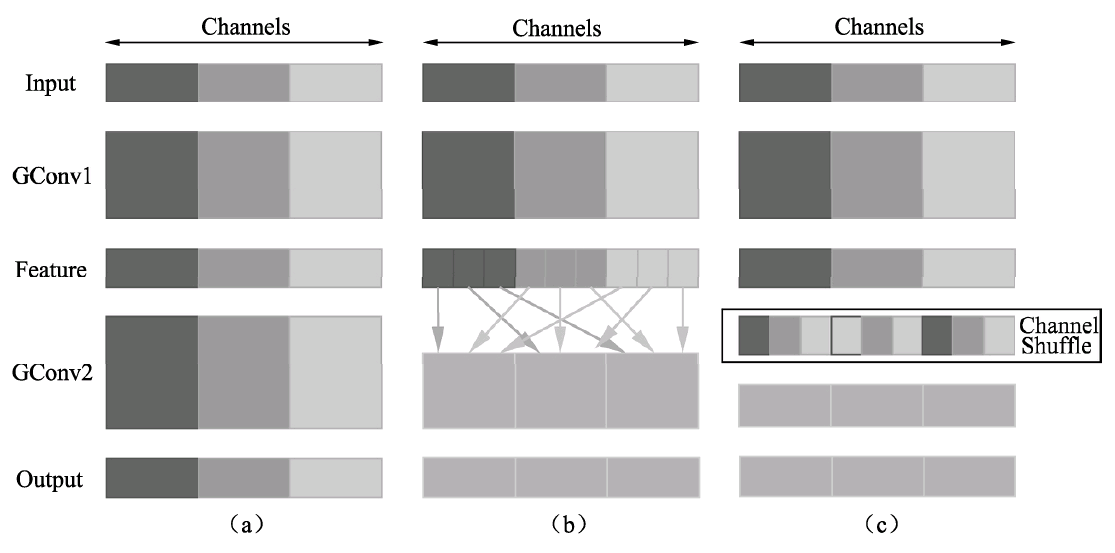
上图中a图代表了常规的两个组卷积操作，可以看到，如果没有逐点的1×1卷积或者通道混洗，最终输出的特征仅由一部分输入通道的特征计算得出，这种操作阻碍了信息的流通，进而降低了特征的表达能力。因此，我们希望在一个组卷积之后，能够将特征图之间的通道信息进行融合，类似于图中b的操作，将每一个组的特征分散到不同的组之后，再进行下一个组卷积，这样输出的特征就能够包含每一个组的特征，而通道混洗恰好可以实现这个过程，如图的c图所示。通道混洗可以通过几个常规的张量操作巧妙地实现，如下图所示。为了更好地讲解实现过程，这里对输入通道做了1~12的编号，一共包含3个组，每个组包含4个通道。

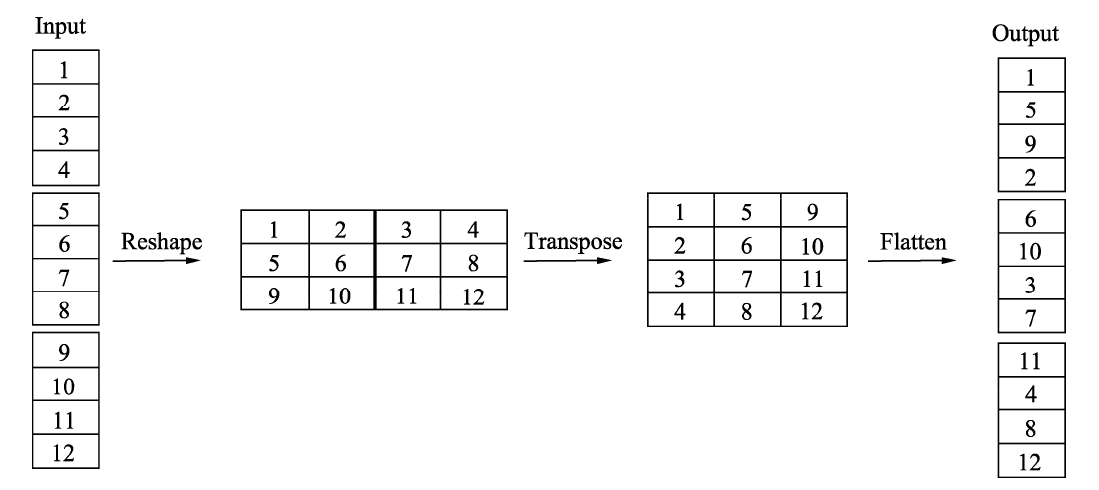
下面详细介绍混洗过程中使用到的3个操作：

Reshape：首先将输入通道一个维度Reshape成两个维度，一个是卷积组数，一个是每个卷积组包含的通道数。
Transpose：将扩展出的两维进行置换。
Flatten：将置换后的通道Flatten平展后即可完成最后的通道混洗。

下面从代码角度讲解一下通道混洗的实现过程。（Pytorch实现）

def channel_shuffle(x, groups):

batchsize, num_channels, height, width = x.data.size()

channels_per_group = num_channels // groups

# Reshape操作，将通道扩展为两维

x = x.view(batchsize, groups, channels_per_group, height, width)

# Transpose操作，将组卷积两个维度进行置换

x = torch.transpose(x, 1, 2).contiguous()

# Flatten操作，两个维度平展成一个维度

x = x.view(batchsize, -1, height, width)

return x

ShuffleNet v1网络结构：

==================

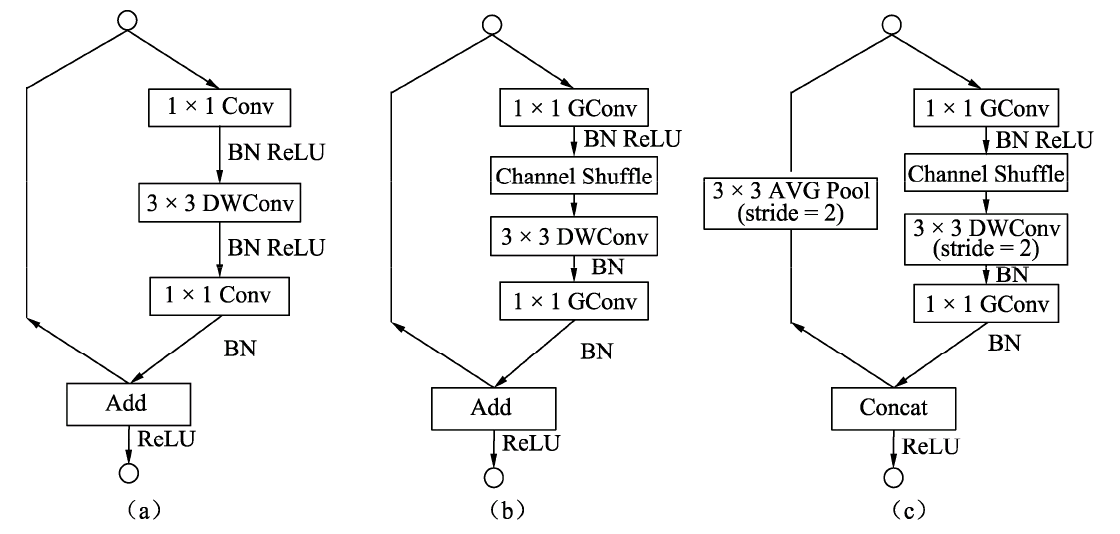
利用上述通道混洗操作，ShuffleNet构建出了如下图所示的网络基本模块。

图的a图是一个带有深度可分离卷积的残差模块，这里的1×1是逐点的卷积。相比深度可分离卷积，1×1计算量较大。
图的b图则是基本的ShuffleNet基本单元，可以看到1×1卷积采用的是组卷积，然后进行通道的混洗，这两步可以取代1×1的逐点卷积，并且大大降低了计算量。3×3卷积仍然采用深度可分离的方式。
图的c图是带有降采样的ShuffleNet单元，在旁路中使用了步长为2的3×3平均池化进行降采样，在主路中3×3卷积步长为2实现降采样。另外，由于降采样时通常要伴有通道数的增加，ShuffleNet直接将两分支拼接在一起来实现了通道数的增加，而不是常规的逐点相加。

得益于组卷积与通道混洗，ShuffleNet的基本单元可以很高效地进行计算。在该基本单元的基础上，ShuffleNet的整体网络结构如下表所示。

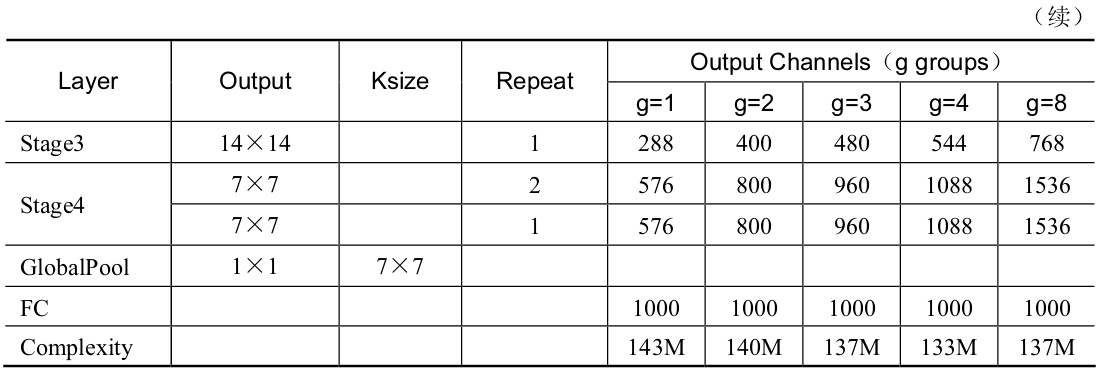
关于ShuffleNet的整体结构，有以下3点需要注意：

g代表组卷积的组数，以控制卷积连接的稀疏性。组数越多，计算量越少，因此在相同的计算资源，可以使用更多的卷积核以获取更多的通道数。
ShuffleNet在3个阶段内使用了其特殊的基本单元，这3个阶段的第一个Block的步长为2以完成降采样，下一个阶段的通道数是上一个的两倍。
深度可分离卷积虽然可以有效降低计算量，但其存储访问效率较差，因此第一个卷积并没有使用ShuffleNet基本单元，而是只在后续3个阶段使用。

下面以g=3为例，从代码层面讲解ShuffleNet网络的构建。（Pytorch实现）

from torch import nn

import torch.nn.functional as F

class ShuffleNet(nn.Module):

def init(self, groups=3, in_channels=3, num_classes=1000):

super(ShuffleNet, self).init()

self.groups = groups

# 3个阶段的Block数量

self.stage_repeats = [3, 7, 3]

self.in_channels = in_channels

self.num_classes = num_classes

# g为3时，每一个阶段输出特征的通道数

self.stage_out_channels = [-1, 24, 240, 480, 960]

self.conv1 = conv3x3(self.in_channels,

self.stage_out_channels[1], # stage 1

stride=2)

self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)

# 单独构建3个阶段

self.stage2 = self._make_stage(2)

self.stage3 = self._make_stage(3)

self.stage4 = self._make_stage(4)

# 全连接层，当前模型用于物体分类

num_inputs = self.stage_out_channels[-1]

self.fc = nn.Linear(num_inputs, self.num_classes)

def _make_stage(self, stage):

modules = OrderedDict()

stage_name = “ShuffleUnit_Stage{}”.format(stage)

# 在第二个阶段之后开始使用组卷积

grouped_conv = stage > 2

# 每个阶段的第一个模块使用的是Concat，因此需要单独构建

first_module = ShuffleUnit(

self.stage_out_channels[stage-1],

self.stage_out_channels[stage],

groups=self.groups,

grouped_conv=grouped_conv,

combine=‘concat’

)

modules[stage_name+“_0”] = first_module

# 重复构建每个阶段剩余的Block模块

for i in range(self.stage_repeats[stage-2]):

name = stage_name + “_{}”.format(i+1)

module = ShuffleUnit(

self.stage_out_channels[stage],

groups=self.groups,

grouped_conv=True,

combine=‘add’

)

modules[name] = module

return nn.Sequential(modules)

def forward(self, x):

x = self.conv1(x)

x = self.maxpool(x)

x = self.stage2(x)

x = self.stage3(x)

x = self.stage4(x)

# 全局的平均池化层

x = F.avg_pool2d(x, x.data.size()[-2:])

# 将特征平展，并送入全连接层与Softmax，得到最终预测概率

x = x.view(x.size(0), -1)

x = self.fc(x)

return F.log_softmax(x, dim=1)

总体上，ShuffleNet提出了一个巧妙的通道混洗模块，在几乎不影响准确率的前提下，进一步地降低了计算量，性能优于ResNet和Xception等网络，因此也更适合部署在移动设备上。

ShuffleNet v2网络结构：

==================

在2018年，旷视的团队进一步升级了ShuffleNet，提出了新的版本ShuffleNet v2。相比于ShuffleNet v1，ShuffleNet v2进一步分析了影响模型速度的因素，提出了新的规则，并基于此规则，改善了原版本的不足。原有的一些轻量化方法在衡量模型性能时，通常使用浮点运算量FLOPs（Floating Point Operations）作为主要指标。FLOPs是指模型在进行一次前向传播时所需的浮点计算次数，其单位为FLOP，可以用来衡量模型的复杂度。 然而，通过一系列实验发现ShuffleNet v2仅仅依赖FLOPs是有问题的，FLOPs近似的网络会存在不同的速度，还有另外两个重要的指标：内存访问时间（Memory Access Cost，MAC）与网络的并行度。 以此作为出发点，ShuffleNet v2做了大量的实验，分析影响网络运行速度的原因，提出了建立高性能网络的4个基本规则： （1）卷积层的输入特征与输出特征通道数相等时，MAC最小，此时模型速度最快。 （2）过多的组卷积会增加MAC，导致模型的速度变慢。 （3）网络的碎片化会降低可并行度，这表明模型中分支数量越少，模型速度会越快。 （4）逐元素（Element Wise）操作虽然FLOPs值较低，但其MAC较高，因此也应当尽可能减少逐元素操作。 以这4个规则为基础，可以看出ShuffleNet v1有3点违反了此规则：