第二章：9.4 softmax的改进实现-减少误差

浮点数精度和数值舍入误差

在计算机中，浮点数（如3.14或0.001）是用二进制形式表示的，这种表示方式只能近似地表示某些十进制小数。由于这种近似，当我们进行数学运算时，尤其是涉及大量小数点后数字的运算，就可能产生数值舍入误差。这些误差可能在多次计算后累积，从而影响最终结果的准确性。

逻辑回归中的数值舍入误差

在逻辑回归中，我们通常使用Sigmoid函数将线性组合 z 转换为概率 a（即激活值），然后计算损失函数。Sigmoid函数的公式是：

虽然这种方法在大多数情况下是有效的，但在某些情况下，如果 z 的值非常大或非常小，计算： e的−z次方  时可能会遇到数值稳定性问题。例如，当 z 非常大时， e的−z次方  会非常接近0，这可能导致在计算 1+ e的−z次方 时， e的−z次方的值被舍入为0，从而使得 a 的计算结果不准确。

Softmax回归中的数值舍入误差

在Softmax回归中，我们使用Softmax函数将一组线性组合 z1​,z2​,...,zn​ 转换为概率分布。Softmax函数的公式是：

这种方法在处理多类分类问题时非常有效，但同样可能遇到数值稳定性问题。特别是当某些 zi​ 的值非常大或非常小，计算 ezi​ 时可能会产生极端值，这可能导致数值溢出或下溢，从而影响最终的概率计算。

减少数值舍入误差的方法

为了减少这些数值舍入误差，我们可以采用以下方法：

1. 直接使用原始输出：

   • 在逻辑回归中，我们可以直接在损失函数中使用 z 而不是 a。这样，TensorFlow可以在内部进行更精确的计算，因为它不需要计算Sigmoid函数，从而避免了可能的数值稳定性问题。

   • 在Softmax回归中，我们同样可以直接在损失函数中使用 z 而不是 a。这允许TensorFlow在内部进行更精确的计算，因为它不需要计算Softmax函数，从而避免了可能的数值稳定性问题。

2. 使用稳定的数学公式：

   • 对于Softmax，可以使用一个更稳定的数学公式来计算，例如通过减去 z 中的最大值来避免 ezi​ 产生极端值。这种方法称为“数值稳定Softmax”。

代码实现

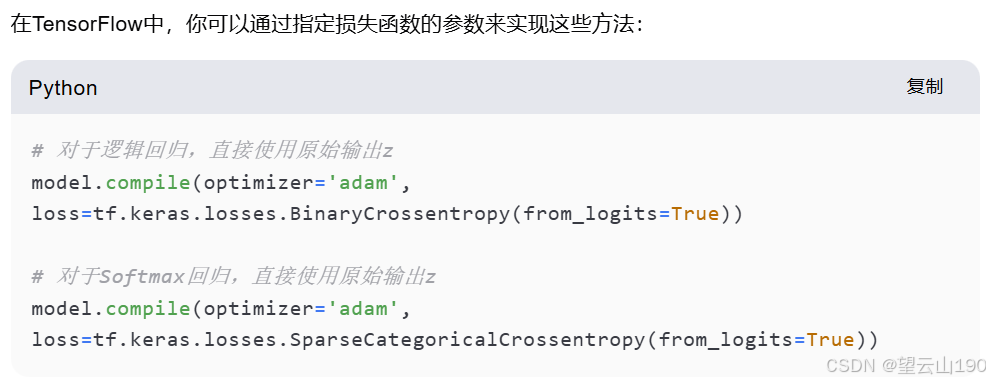
通过这种方式，你可以告诉TensorFlow在计算损失函数时直接使用原始输出 z，而不是先计算激活值或概率。这不仅减少了数值舍入误差，还可以提高计算效率。

---

---

图片1：数值舍入误差与逻辑回归

这张图片主要讲解了在逻辑回归中如何通过更精确的数学实现来减少数值舍入误差。

• 模型结构：

  • 使用Sequential模型，包含两个ReLU激活的隐藏层和一个Sigmoid激活的输出层。

• 模型编译：

  • 使用BinaryCrossentropy()作为损失函数，并设置from_logits=True，指示损失函数直接使用logits（即未经过Sigmoid转换的原始输出）。

---

图片2：Softmax回归的数值精度

• 主题：展示如何通过更精确的数学实现来减少Softmax回归中的数值舍入误差。

• Softmax回归公式：

  • 激活函数 (a1​,...,a10​)=g(z1​,...,z10​)。

• 

• 模型结构：

  • 使用Sequential模型，包含两个ReLU激活的隐藏层和一个Softmax激活的输出层。

• 模型编译：

  • 使用SparseCategoricalCrossentropy()作为损失函数。

  • 使用from_logits=True参数，指示损失函数直接使用logits。

---

图片 3: MNIST数据集的更精确实现

• 主题：展示如何在MNIST数据集上实现更精确的Softmax回归。

• 模型结构：

  • 使用Sequential模型，包含两个ReLU激活的隐藏层和一个线性激活的输出层。

• 损失函数：

  • 使用SparseCategoricalCrossentropy(from_logits=True)，直接使用logits计算损失。

• 模型训练：

  • 使用model.fit(X, Y, epochs=100)进行训练。

• 预测：

  • 使用logits = model(X)获取logits，然后通过f_x = tf.nn.softmax(logits)计算Softmax概率。

---

图片 4: 逻辑回归的更精确实现

• 主题：展示如何在逻辑回归中实现更精确的损失计算。

• 模型结构：

  • 使用Sequential模型，包含两个Sigmoid激活的隐藏层和一个线性激活的输出层。

• 损失函数：

  • 使用BinaryCrossentropy(from_logits=True)，直接使用logits计算损失。

• 模型训练：

  • 使用model.fit(X, Y, epochs=100)进行训练。

• 预测：

  • 使用logit = model(X)获取logits，然后通过f_x = tf.nn.sigmoid(logit)计算Sigmoid概率。