图像识别技术与应用学习总结③

一.感知机

x是输入

w称为权重：控制输入信号的重要性的参数

b称为偏置：偏置是调整神经元被激活的容易程度参数

感知机应用:简单逻辑电路

公式:

 

• 与门

 

 真值表:(全1，y＝1)

 

• 与非门

真值表:(y值跟非门的y值相反)

 

• 或门

真值表:(有1，y便等于1)

 

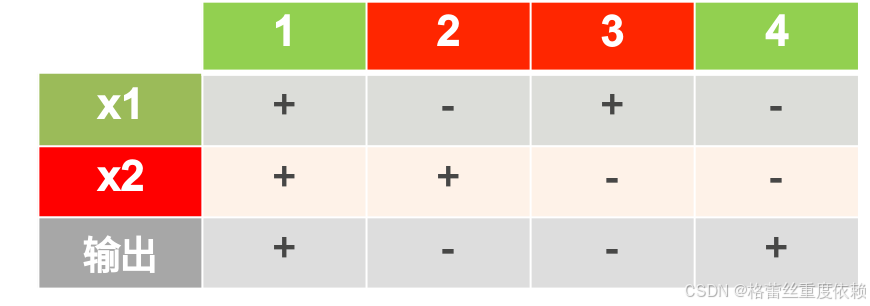
• 异或门

真值表:(没总结出来)

 感知机的局限性:

 

感知机的局限性:感知机的局限性就是只能表示由一条直线分割的空间。

面对这种线性不可分的情况该怎么办呢？用非线性的曲线划分出非线性空间

(多层感知机：最简单的深度神经网络）

多层感知机:

 

 

 二.单隐藏层

• 单分类

 注:σ为激活函数

三.激活函数

 

激活函数：刚才登场的h（x）函数会将输入信号的总和转换为输出信号，这种函数一般称为激活函数（activation function）。

如“激活”一词所示，激活函数的作用在于决定如何来激活输入信号的总和。

激活函数需要具备以下几点性质：

（1） 连续并可导（允许少数点上不可导）的非线性函数。

（2） 激活函数及其导函数要尽可能的简单，有利于提高网络计算效率。

（3） 激活函数的导函数的值域要在一个合适的区间内，不能太大也不能太小，否则会影响训练的效率和稳定性。

• 阶跃函数

 

 (可以说感知机使用了阶跃函数作为激活函数)

• S型（sigmoid）激活函数（挤压函数）

 

(将输入投影到（0，1），是一个软的）

 

• tanh激活函数（双曲正切）

将输入映射到 (-1, 1)

 

• RELU函数（线性修正函数）

ReLU: 线性修正单元

 多分类:

 

多个隐藏层多类分类:

 

 

• 超参数:

         隐藏层数量,多少层隐藏层

         每层的隐藏单元数目，隐藏层神经元个数

五.参数更新

 

前向传播（正向传播）:

输入样本－－输入层－－各隐藏层－－输出层

反向传播（误差反传）:

输出层——各隐藏层——输入层

计算神经网络参数梯度的方法

修正各层单元的权值

六.训练误差和泛化误差

训练误差：模型在训练数据集上的误差

泛化误差: 模型在新数据集上的误差

示例：使用历年试真题准备将来的考试

再历年考试真题取得好成绩（训练误差）并不能保证未来考试成绩更好（泛化误差）

学生A 通过死记硬背学习在历年真题考试中取得好成绩

学生B理解并给出答案的解释

七.过拟合和欠拟合

 

过拟合:当学习器把训练样本学得"太好"了的时候，很可能已经把训练样本自身的一些特点当作了所有潜在样本都会具有的一般性质。

欠拟合:对训练样本的一般性质尚未学好。

模型复杂度的影响:

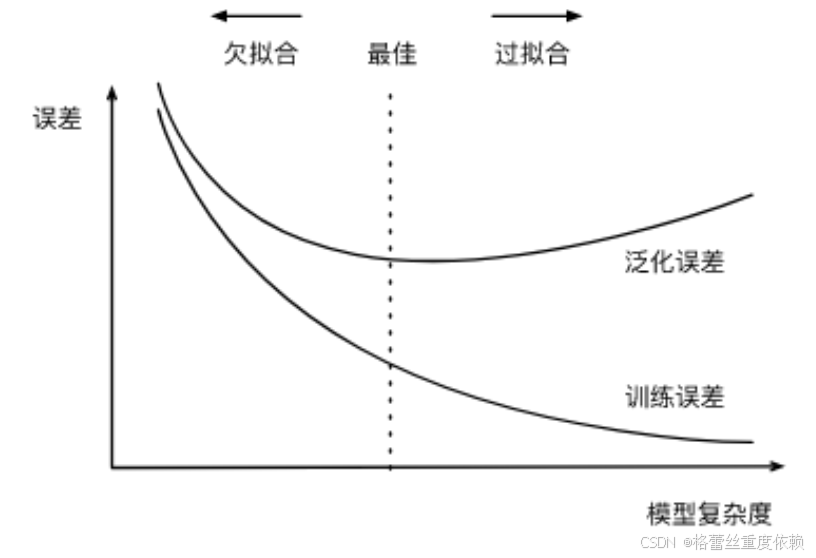
权重衰减

暂退法（丢弃法）

多种因素很重要：

1. 样本数量
2. 每个样本中的特征数量
3. 时间、空间结构
4. 多样性

今天的学习总结就结束啦(｡>∀<｡)