3.4代码随想录第八天打卡

151.翻转字符串里的单词

(1)题目描述:

(2)解题思路:

1.简单的反转字符串功能

// 反转字符串s中左闭右闭的区间[start, end]
void reverse(string& s, int start, int end) {
    for (int i = start, j = end; i < j; i++, j--) {
        swap(s[i], s[j]);
    }
}

2.去除冗余空格

void removeExtraSpaces(string& s) {//去除所有空格并在相邻单词之间添加空格, 快慢指针。
    int slow = 0;   //整体思想参考https://programmercarl.com/0027.移除元素.html
    for (int i = 0; i < s.size(); ++i) { //
        if (s[i] != ' ') { //遇到非空格就处理，即删除所有空格。
            if (slow != 0) s[slow++] = ' '; //手动控制空格，给单词之间添加空格。slow != 0说明不是第一个单词，需要在单词前添加空格。
            while (i < s.size() && s[i] != ' ') { //补上该单词，遇到空格说明单词结束。
                s[slow++] = s[i++];
            }
        }
    }
    s.resize(slow); //slow的大小即为去除多余空格后的大小。
}

(3)总结:

1.空间复杂度是O(1)是在原本的字符串中改变

2.只有在slow不位于最开头时，才会向slow中手动填空格，fast指针忽视所有空格，向slow指针位置填值

3.先整体反转字符串，再反转各个单词

class Solution {
public:
    void reverse(string& s, int start, int end){ //翻转，区间写法：左闭右闭 []
        for (int i = start, j = end; i < j; i++, j--) {
            swap(s[i], s[j]);
        }
    }

    void removeExtraSpaces(string& s) {//去除所有空格并在相邻单词之间添加空格, 快慢指针。
        int slow = 0;   //整体思想参考https://programmercarl.com/0027.移除元素.html
        for (int i = 0; i < s.size(); ++i) { //
            if (s[i] != ' ') { //遇到非空格就处理，即删除所有空格。
                if (slow != 0) s[slow++] = ' '; //手动控制空格，给单词之间添加空格。slow != 0说明不是第一个单词，需要在单词前添加空格。
                while (i < s.size() && s[i] != ' ') { //补上该单词，遇到空格说明单词结束。
                    s[slow++] = s[i++];
                }
            }
        }
        s.resize(slow); //slow的大小即为去除多余空格后的大小。
    }

    string reverseWords(string s) {
        removeExtraSpaces(s); //去除多余空格，保证单词之间之只有一个空格，且字符串首尾没空格。
        reverse(s, 0, s.size() - 1);
        int start = 0; //removeExtraSpaces后保证第一个单词的开始下标一定是0。
        for (int i = 0; i <= s.size(); ++i) {
            if (i == s.size() || s[i] == ' ') { //到达空格或者串尾，说明一个单词结束。进行翻转。
                reverse(s, start, i - 1); //翻转，注意是左闭右闭 []的翻转。
                start = i + 1; //更新下一个单词的开始下标start
            }
        }
        return s;
    }
};

 卡码网：55.右旋转字符串

(1)题目描述:

(2)解题思路:

1.版本一：对应下方总结

// 版本一
#include<iostream>
#include<algorithm>
using namespace std;
int main() {
    int n;
    string s;
    cin >> n;
    cin >> s;
    int len = s.size(); //获取长度

    reverse(s.begin(), s.end()); // 整体反转
    reverse(s.begin(), s.begin() + n); // 先反转前一段，长度n
    reverse(s.begin() + n, s.end()); // 再反转后一段

    cout << s << endl;

} 

2.版本二：对应下方总结

// 版本二 
#include<iostream>
#include<algorithm>
using namespace std;
int main() {
    int n;
    string s;
    cin >> n;
    cin >> s;
    int len = s.size(); //获取长度
    reverse(s.begin(), s.begin() + len - n); // 先反转前一段，长度len-n ，注意这里是和版本一的区别
    reverse(s.begin() + len - n, s.end()); // 再反转后一段
    reverse(s.begin(), s.end()); // 整体反转
    cout << s << endl;

}

(3)总结:

1.通过 整体倒叙，把两段子串顺序颠倒，两个段子串里的的字符在倒叙一把，负负得正，这样就不影响子串里面字符的顺序了

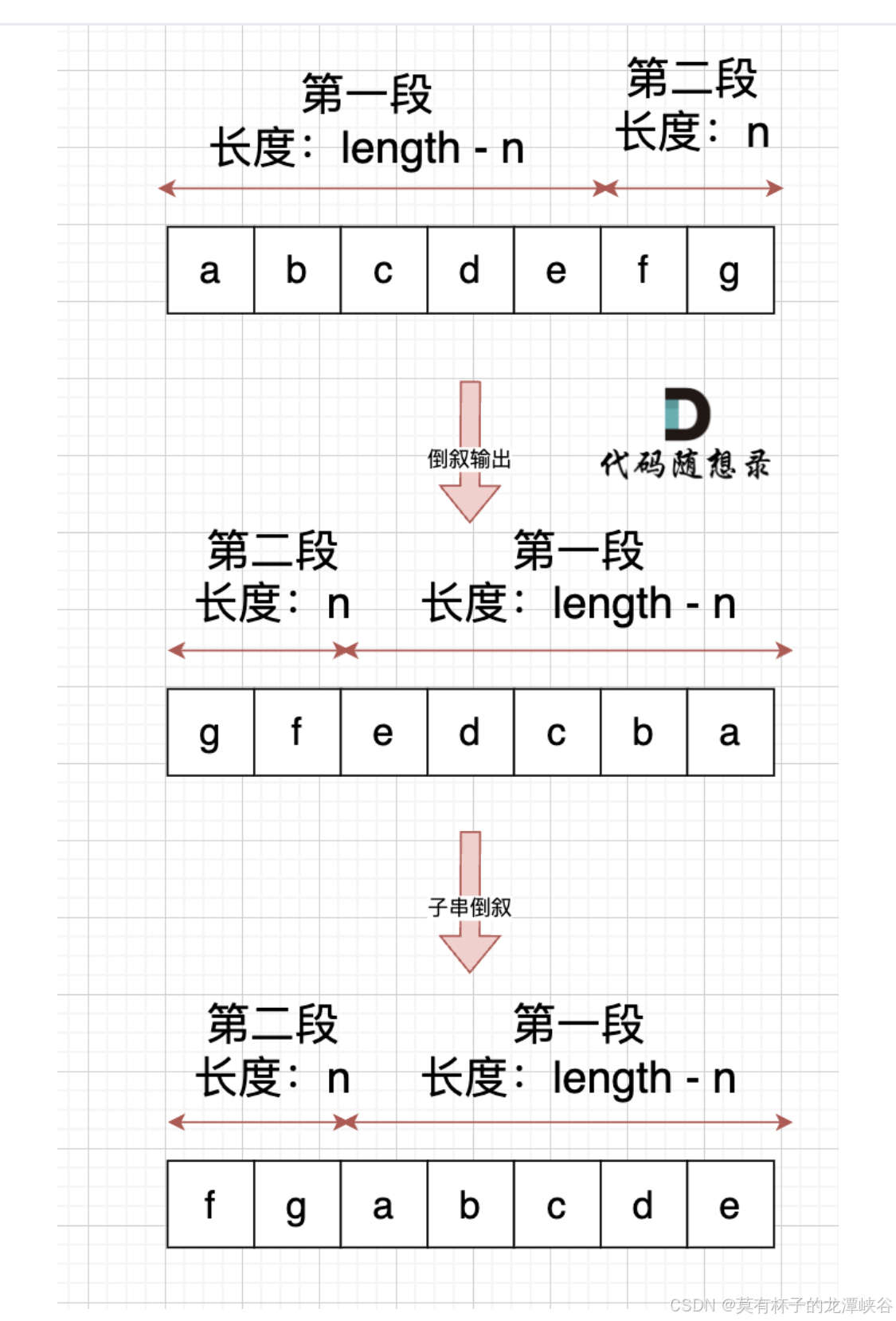
2.第二种思路：先局部反转再再调换位置

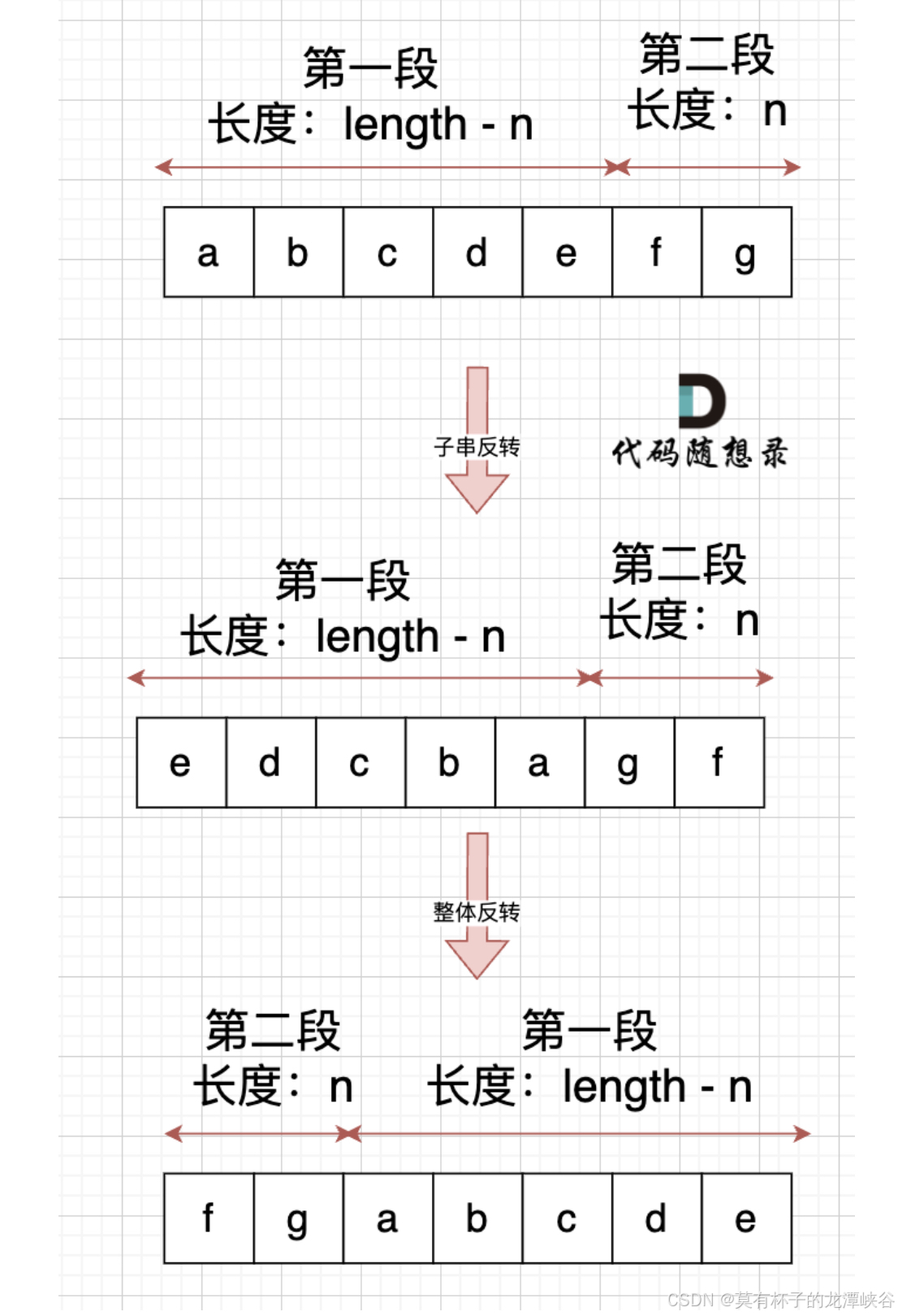
28.实现 strStr()

(1)题目描述:

(2)准备:

1.KMP算法是什么:KMP的主要思想是当出现字符串不匹配时，可以知道一部分之前已经匹配的文本内容，可以利用这些信息避免从头再去做匹配了。

2.前缀表就是告知下一步匹配模式串跳到哪个位置，next数组就是一个前缀表，前缀表是用来回退的，它记录了模式串与主串(文本串)不匹配的时候，模式串应该从哪里开始重新匹配。 

3.上图f无法与文本串中的b匹配，那就重新寻找模式串中的b与之匹配。

4.前缀是什么:指不包含最后一个字符的所有以第一个字符开头的连续子串(如aabaaf的前缀有a、aa、aab、aaba、aabaa)

5.后缀是什么:指不包含第一个字符的所有以最后一个字符结尾的连续子串

6.最长相等前后缀

那么aabaaf的前缀表就是010120

2表示最长相等前后缀的长度，所以跳到了字符串中下标为 2的位从而找到了b

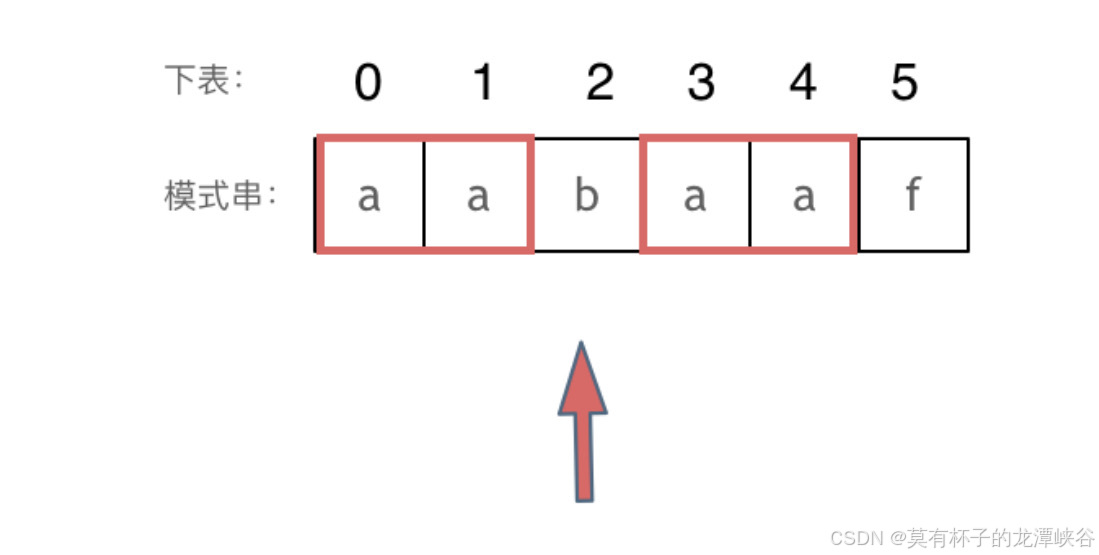
7.next数组就可以是前缀表，但是很多实现都是把前缀表统一减一（右移一位，初始位置为-1）之后作为next数组。

（3）解题思路：

class Solution {
public:
    void getNext(int* next, const string& s) {
        int j = 0;
        next[0] = 0;
        for(int i = 1; i < s.size(); i++) {
            while (j > 0 && s[i] != s[j]) {
                j = next[j - 1];
            }
            if (s[i] == s[j]) {
                j++;
            }
            next[i] = j;
        }
    }
    int strStr(string haystack, string needle) {
        if (needle.size() == 0) {
            return 0;
        }
        vector<int> next(needle.size());
        getNext(&next[0], needle);
        int j = 0;
        for (int i = 0; i < haystack.size(); i++) {
            while(j > 0 && haystack[i] != needle[j]) {
                j = next[j - 1];
            }
            if (haystack[i] == needle[j]) {
                j++;
            }
            if (j == needle.size() ) {
                return (i - needle.size() + 1);
            }
        }
        return -1;
    }
};

（4）总结：

1.next数组可以有三种写法(普通前缀表、前缀表右移补-1或前缀表中数均减1)(最后一种跳到b是找表中倒数第二个数(为1)+1为2跳到下标为二的地方)

2.j表示前缀末尾i表示后缀末尾(j在ⅰ前)

3.前后缀不相同的情况:遇见冲突ⅰ和j不匹配时看前一位j回退到前一位

4.前后缀相同的情况(如都为a)

void getNext(int* next, const string& s) {
        int j = 0;
        next[0] = 0;
        for(int i = 1; i < s.size(); i++) {
            while (j > 0 && s[i] != s[j]) { // j要保证大于0，因为下面有取j-1作为数组下标的操作
                j = next[j - 1]; // 注意这里，是要找前一位的对应的回退位置了
            }
            if (s[i] == s[j]) {
                j++;
            }
            next[i] = j;
        }
    }

459.重复的子字符串

(1)题目描述:

(2)解题思路:

1.移动匹配

class Solution {
public:
    bool repeatedSubstringPattern(string s) {
        string t = s + s;
        t.erase(t.begin()); t.erase(t.end() - 1); // 掐头去尾
        if (t.find(s) != std::string::npos) return true; // r
        return false;
    }
};

2.KMP前缀表（不减一）

class Solution {
public:
    void getNext (int* next, const string& s){
        next[0] = 0;
        int j = 0;
        for(int i = 1;i < s.size(); i++){
            while(j > 0 && s[i] != s[j]) {
                j = next[j - 1];
            }
            if(s[i] == s[j]) {
                j++;
            }
            next[i] = j;
        }
    }
    bool repeatedSubstringPattern (string s) {
        if (s.size() == 0) {
            return false;
        }
        int next[s.size()];
        getNext(next, s);
        int len = s.size();
        if (next[len - 1] != 0 && len % (len - (next[len - 1] )) == 0) {
            return true;
        }
        return false;
    }
};

(3)总结:

1.移动匹配
abcabc，内部由重复的子串组成，那么这个字符串的结构一定是这样的，也就是由前后相同的子串组成。

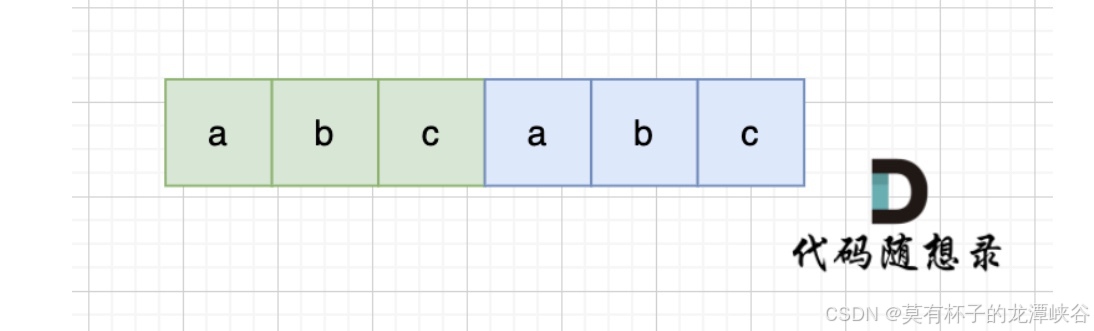
那么既然前面有相同的子串，后面有相同的子串，用 s + s，这样组成的字符串中，后面的子串做前串，前面的子串做后串，就一定还能组成一个s

2.如果有一个字符串s，在 s + s 拼接后， 不算首尾字符，如果能凑成s字符串，说明s 一定是重复子串组成
3.用KMP方法