1. 图的基本概念
图的相关概念可结合视频学习
图的定义:
 有向图和无向图:
有向图和无向图:
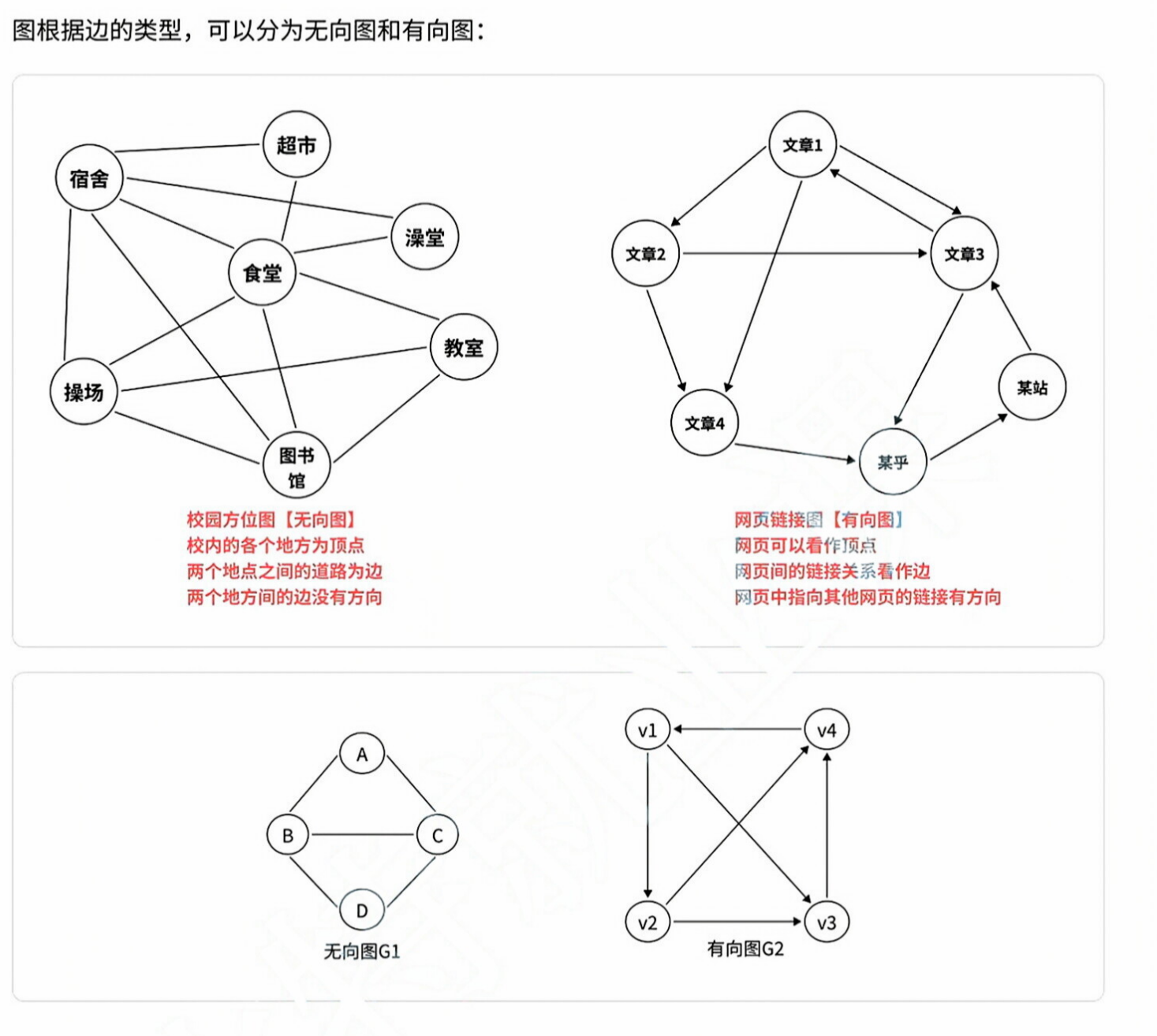
简单图和多重图:
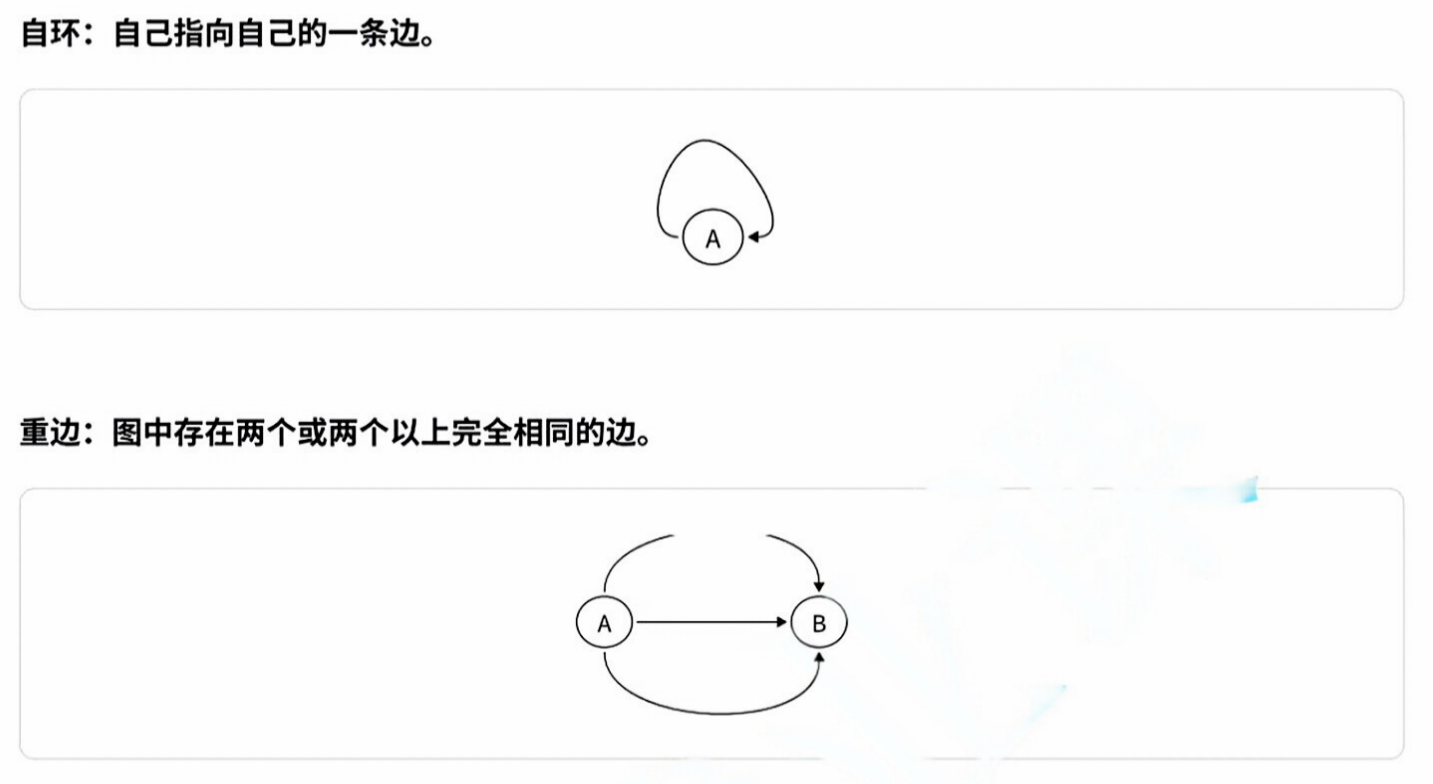
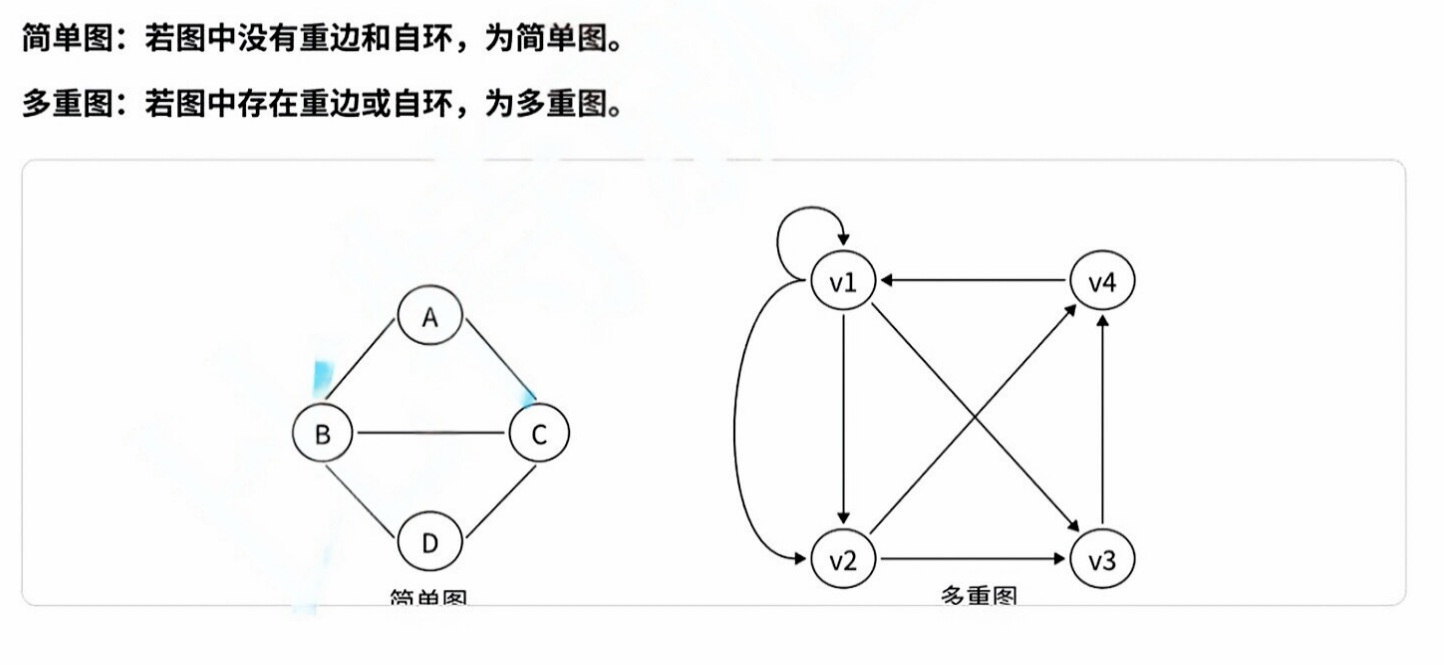
稠密图和稀疏图:
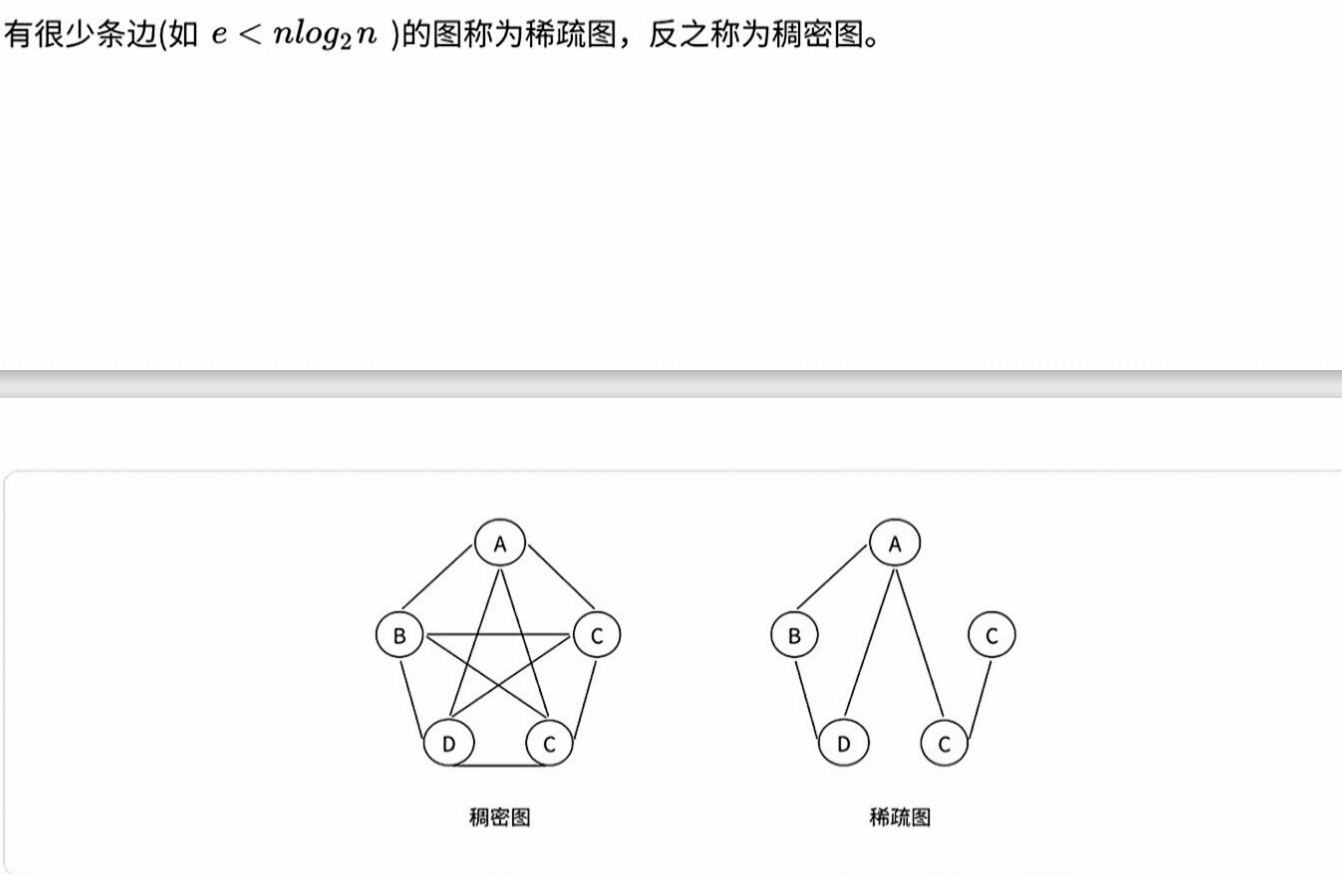
顶点的度:
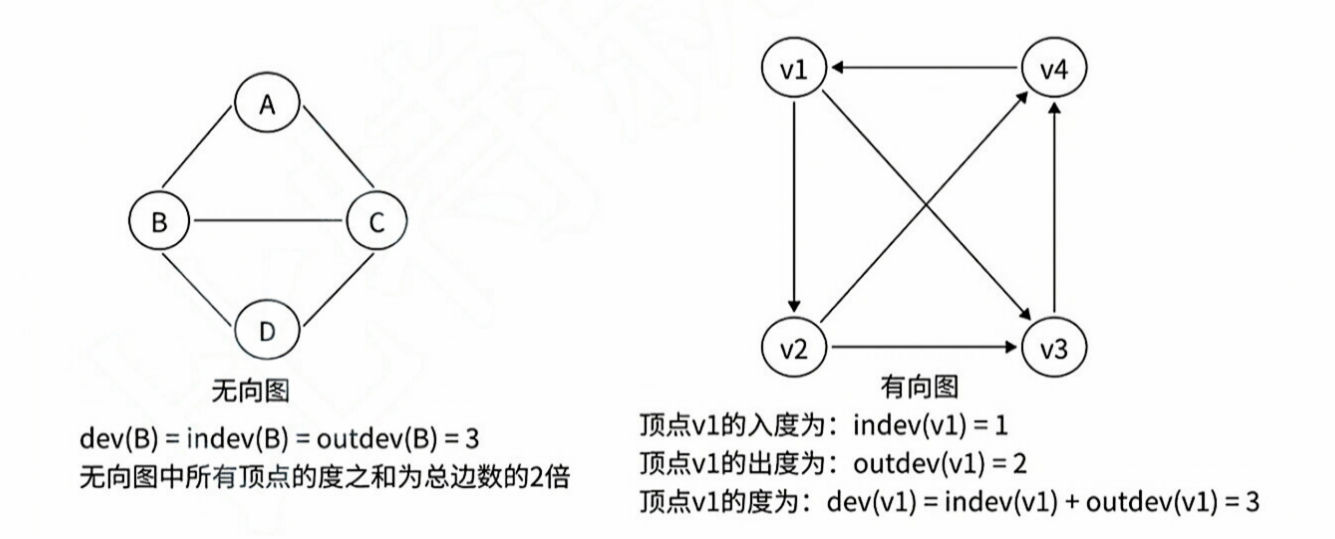
顶点 v 的度是指与它相关联的边的条数,记作 deg(v)。由该顶点发出的边称为顶点的出度,到达该顶 点的边称为顶点的⼊度。
• 无向图中,顶点的度等于该顶点的⼊度(indev)和出度(outdev),即 deg(v) = indeg(v) =
outdeg(v)。
• 有向图中,顶点的度等于该顶点的⼊度与出度之和,其中顶点 v 的⼊度 indeg(v) 是以 v 为终点的有
向边的条数,顶点 v 的出度 outdeg(v) 是以 v 为起始点的有向边的条数,deg(v) = indeg(v) +
outdeg(v)。
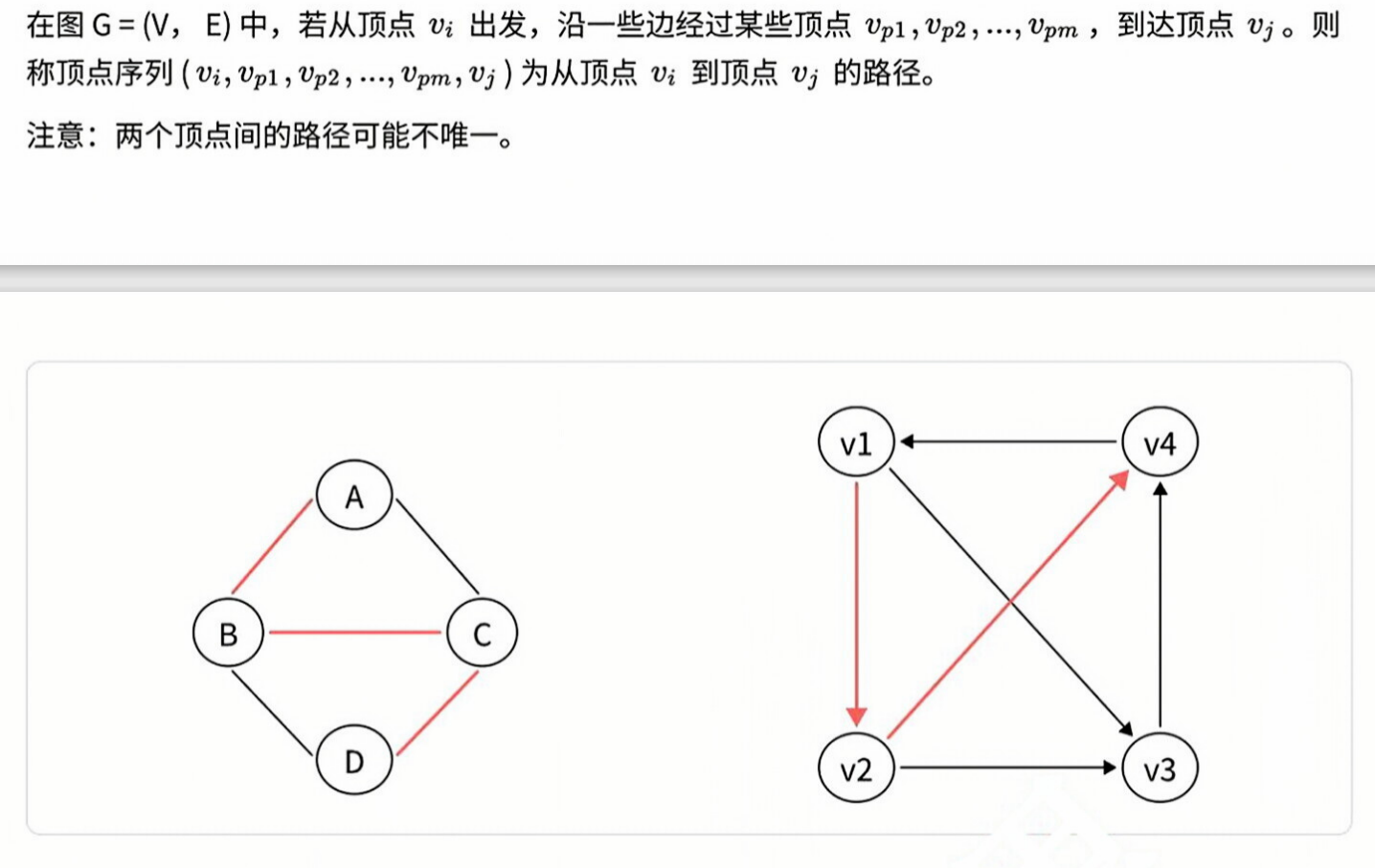
路径:
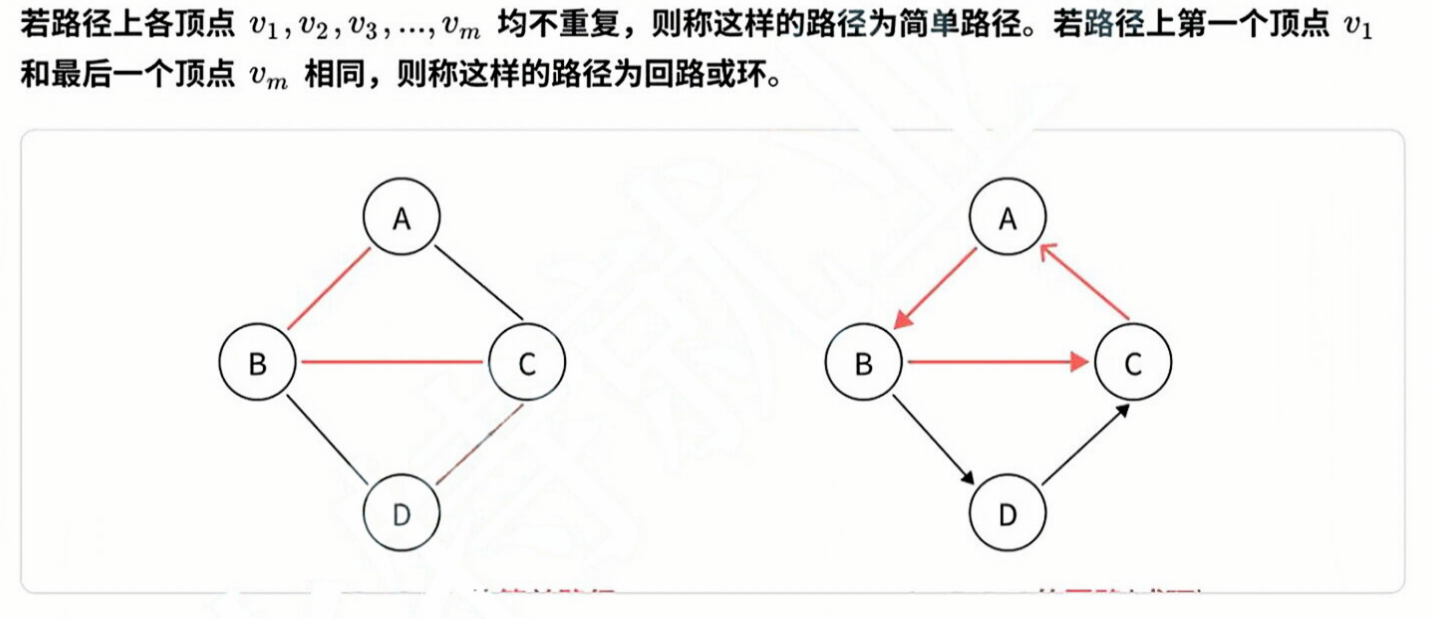
简单路径和回路:
路径长度和带权路径长度:
某些图的边具有与它相关的数值,称其为该边的权值。这些权值可以表⽰两个顶点间的距离、花费的代价、所需的时间等。一边将该种带权图称为网络。
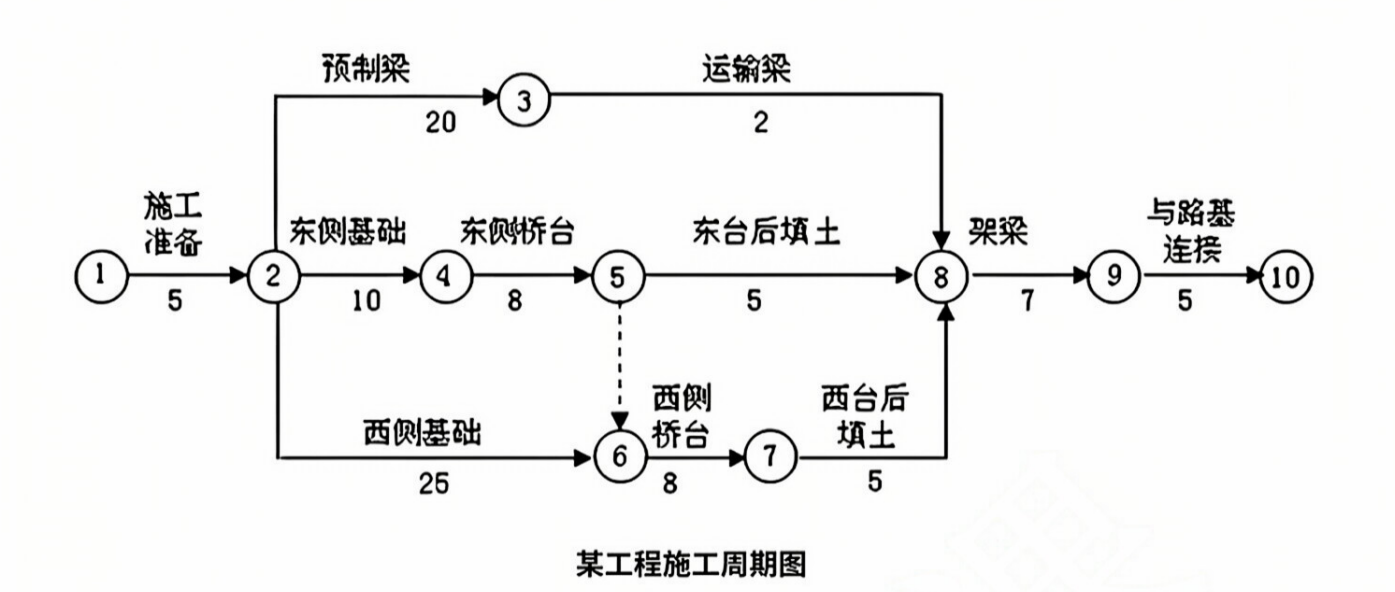
对于不带权的图,⼀条路径的路径⻓度是指该路径上的边的条数。
对于带权的图,⼀条路径的路径⻓度是指该路径上各个边权值的总和
子图:
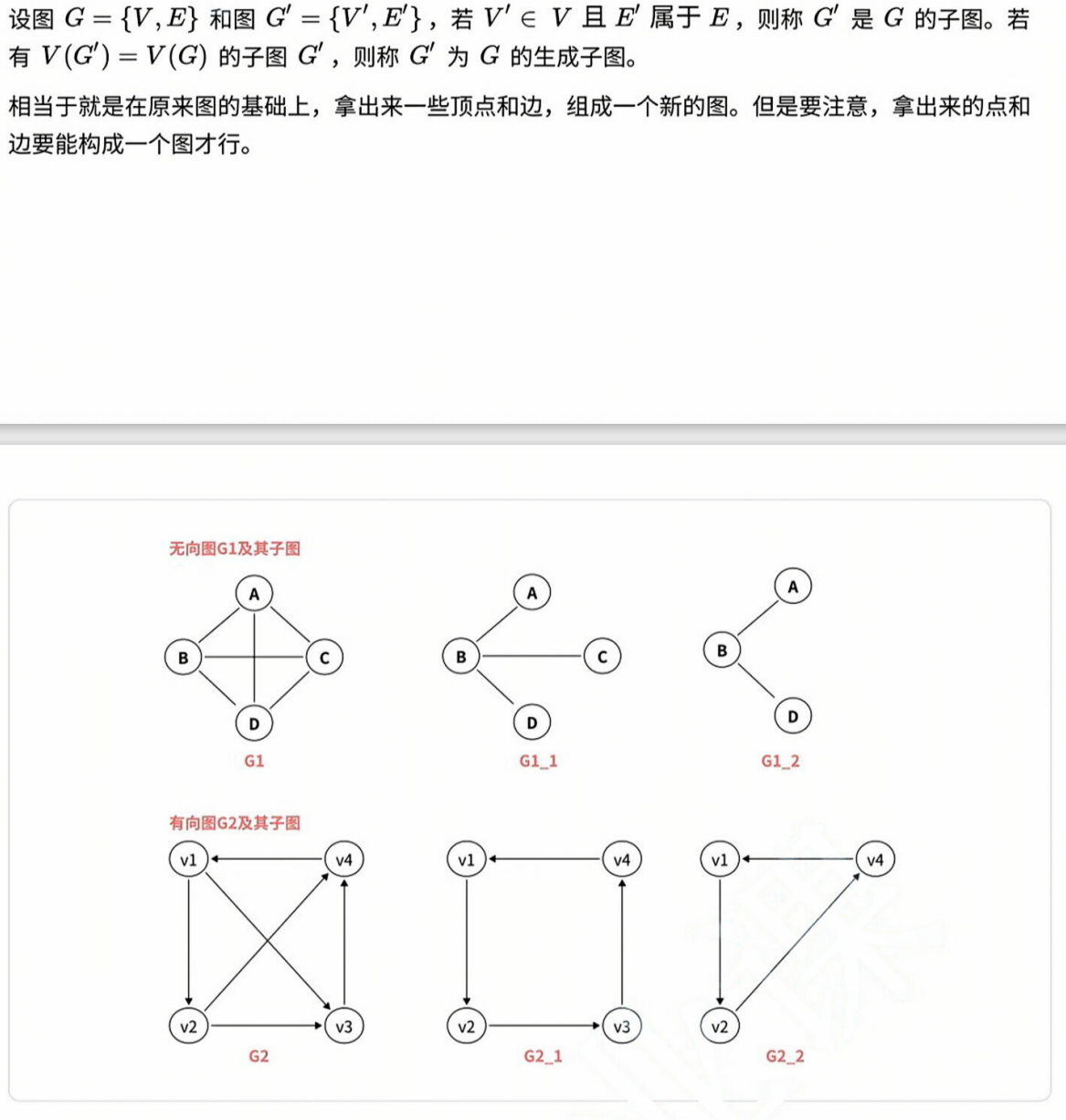
G1_1 和 G1_2 为⽆向图 G1 的⼦图,G1_1 为 G1 的生成子图。
G2_1 和 G2_2 为有向图 G2 的⼦图,G2_1 为 G2 的生成子图。
连通图与联通分量:

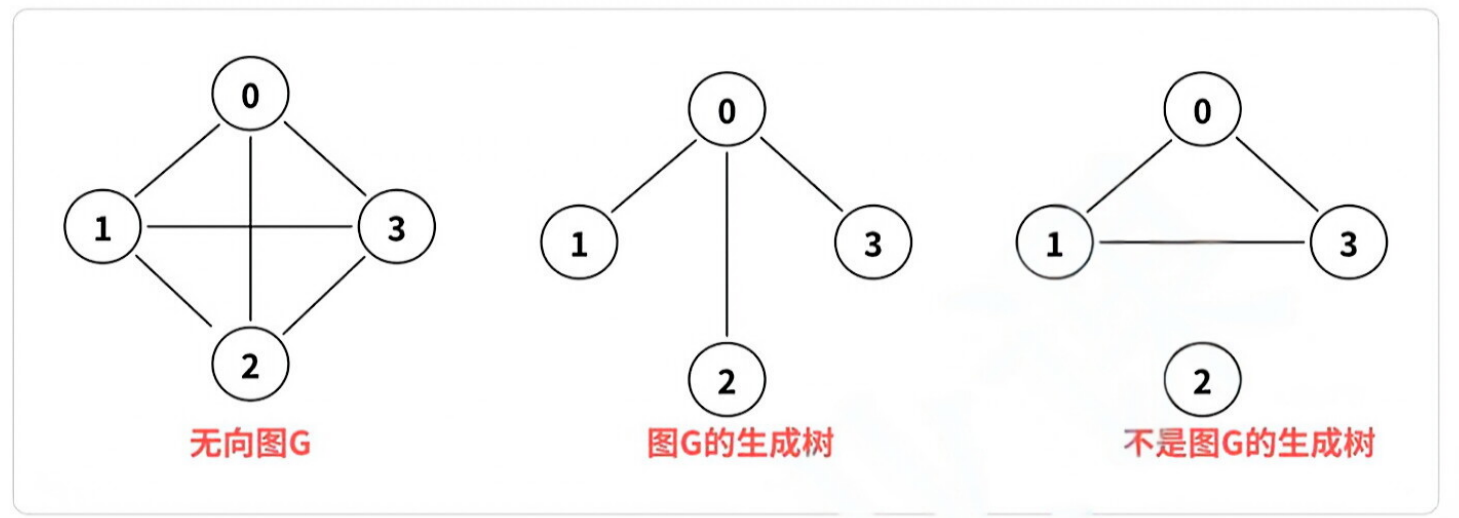
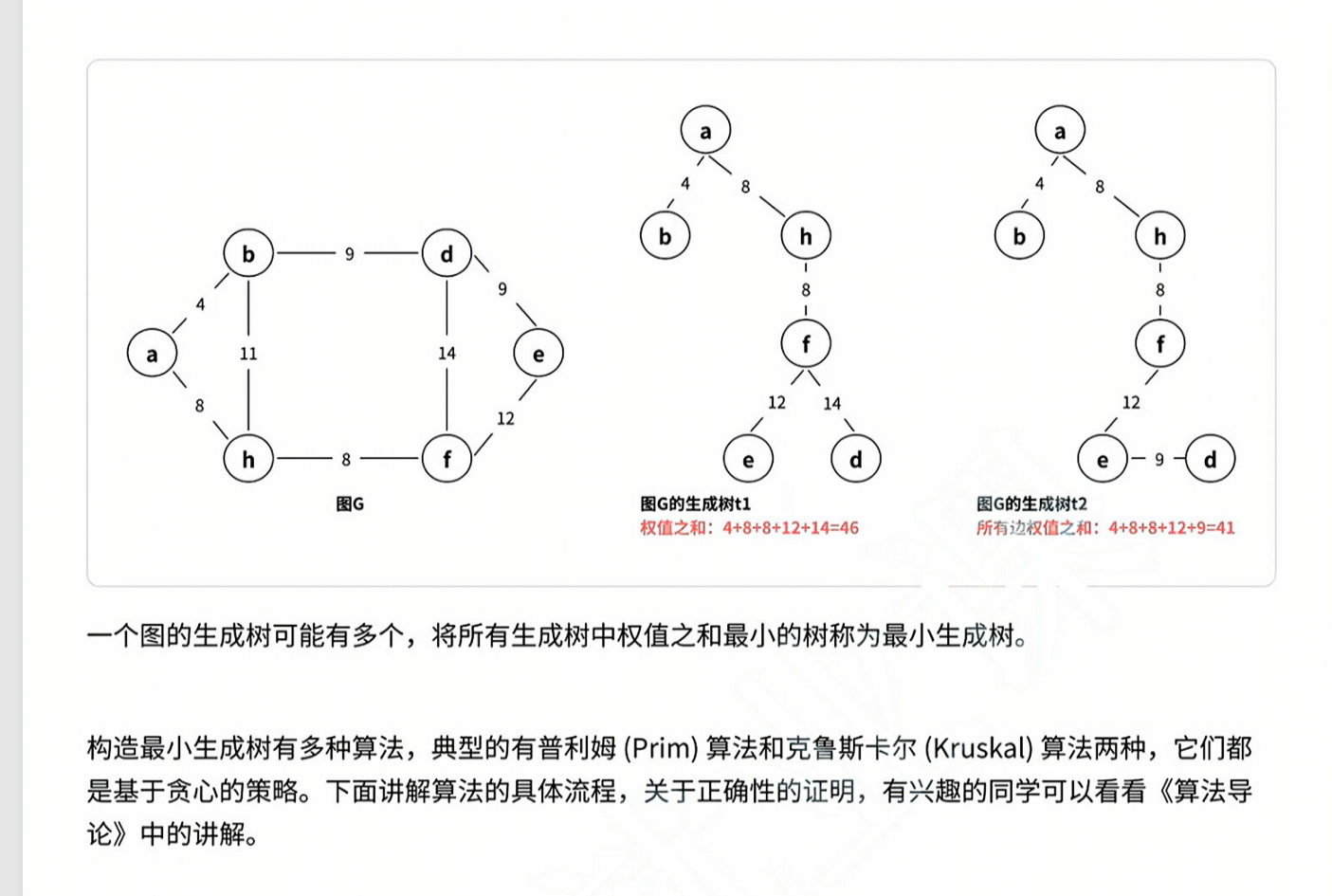
生成树:
连通图的⽣成树是包含图中全部顶点的⼀个极⼩连通⼦图。若图中顶点数为 n,则它的⽣成树含有 n -1 条边。对⽣成树⽽⾔,若砍去⼀条边,则会变成⾮连通图,若加上⼀条边则会形成⼀个回路。
图的存储和遍历:
图的存储有两种:邻接矩阵和邻接表:
• 其中,邻接表的存储⽅式与树的孩⼦表⽰法完全⼀样。因此,⽤ vector 数组以及链式前向星就能实
现。
• 而邻接矩阵就是⽤⼀个⼆维数组,其中 edges[i][j] 存储顶点 i 与顶点 j 之间,边的信
息。
邻接矩阵:
邻接矩阵,指⽤⼀个矩阵(即⼆维数组)存储图中边的信息(即各个顶点之间的邻接关系),存储顶点之间
邻接关系的矩阵称为邻接矩阵。
对于带权图⽽⾔,若顶点 vi和vj 之间有边相连,则邻接矩阵中对应项存放着该边对应的权值,若顶
点 vi和 vj不相连,则⽤∞来代表这两个顶点之间不存在边。
对于不带权的图,可以创建⼀个⼆维的 bool 类型的数组,来标记顶点 vi 和 vj 之间有边相连。
#include<iostream>
#include<cstring>
using namespace std;
const int N = 1010;
int n, m;//顶点个数 边数
int edges[N][N];
int main()
{
memset(edges, -1, sizeof edges);
cin >> n >> m;
for (int i = 1; i <= m; i++)
{
int a, b, c; cin >> a >> b >> c;
edges[a][b] = c;
//a-b有一条边,权值为c
//如果是无向图的话,需要反存
edges[b][a] = c;
}
return 0;
}
vector 数组:
和树的存储⼀模⼀样,只不过如果存在边权的话,我们的 vector 数组⾥⾯放⼀个结构体或者是 pair 即可。
const int N = 1e5 + 10;
typedef pair<int, int>PII;
int n, m;
vector<PII>edges[N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
int a, b, c; cin >> a >> b >> c;
edges[a].push_back({ b,c });
//如果是无向图的话,需要反存
edges[b].push_back({ a,c });
}
}
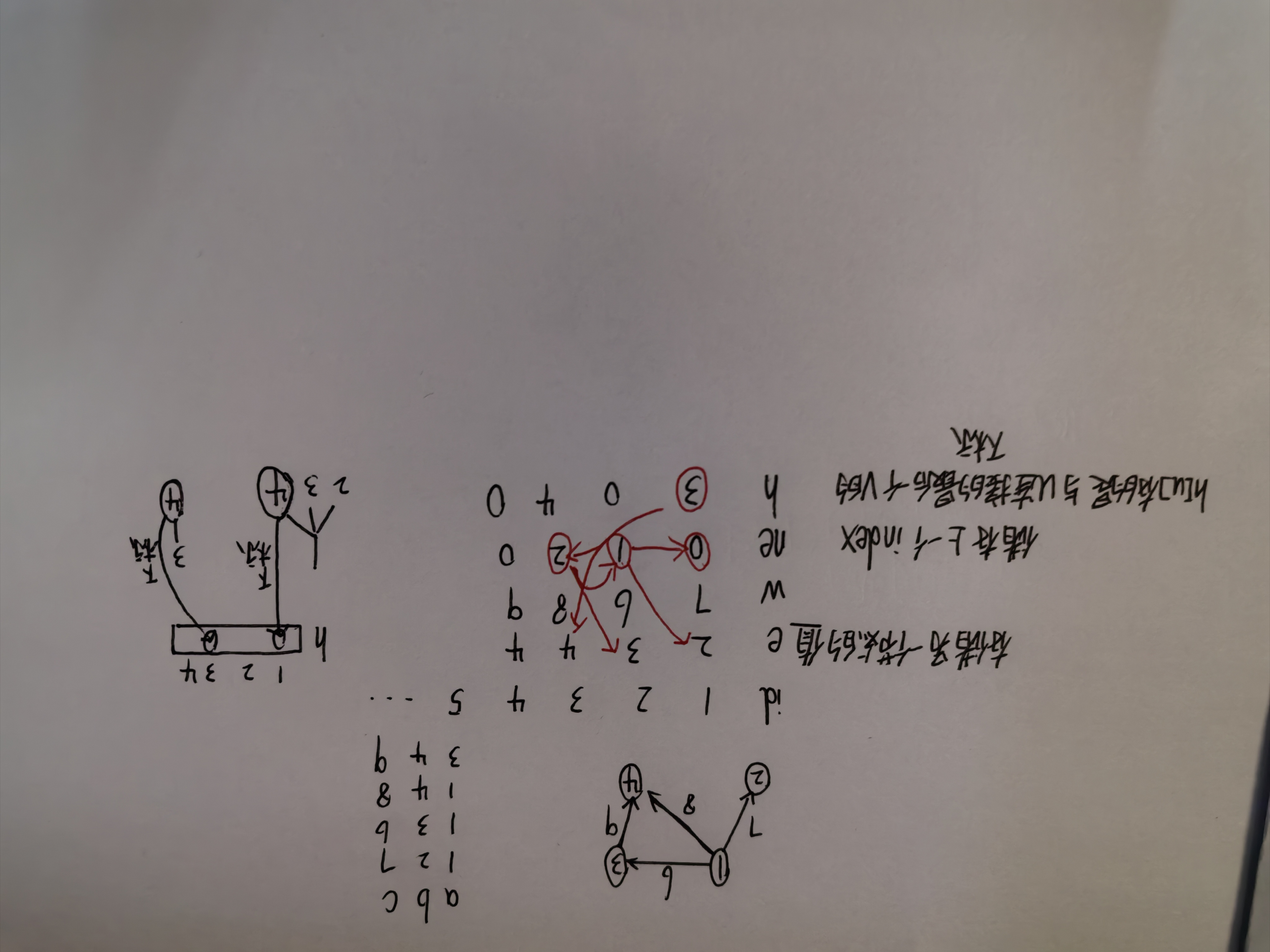
链式前向星:
和树的存储⼀模⼀样,只不过如果存在边权的话,我们多创建⼀维数组,⽤来存储边的权值即可。
//链式前向星
const int N = 1e5 + 10;
int h[N], e[2 * N], w[2 * N], ne[2 * N], id;
//h[a]存储与a节点相连的最后一个下标 e[id]存储第id个 另一个端点b
//w[id]存储第id个权值 ne[id]存储上一个下标
int n, m;
void add(int a, int b, int c)
{
id++;
e[id] = b;
w[id] = c;
ne[id] = h[a];
h[a] = id;
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= m; i++)
{
int a, b, c; cin >> a >> b >> c;
add(a, b, c);
//无向图反存
add(b, a, c);
}
}
图的遍历分两种:DFS 和 BFS,和树的遍历方式以及实现⽅式完全⼀样。因此,可以仿照树这个数据 结构来学习。
DFS和BFS:
1.邻接矩阵
#include<iostream>
#include<cstring>
using namespace std;
const int N = 1010;
int n, m;//顶点个数 边数
int edges[N][N];
bool st[N];
void dfs(int u) //u表示第一个端点,v表示第二个端点
{
cout << u << endl;
st[u] = true;
for (int v = 1; v <= n; v++)
{
if (edges[u][v] != -1 && st[v] == false)//也可写为!st[v]
{
dfs(v);
}
}
}
void bfs(int u)
{
queue<int>q;
q.push(u);
st[u] = true;
while (q.size())
{
int t = q.front(); q.pop();
cout << t << endl;
for (int i = 1; i <= n; i++)
{
if (edges[t][i] != -1 && !st[i])
{
q.push(i);
st[i] = true;
}
}
}
}
int main()
{
memset(edges, -1, sizeof edges);
cin >> n >> m;
for (int i = 1; i <= m; i++)
{
int a, b, c; cin >> a >> b >> c;
edges[a][b] = c;
//a-b有一条边,权值为c
//如果是无向图的话,需要反存
edges[b][a] = c;
}
return 0;
}
2.vector数组
const int N = 1e5 + 10;
typedef pair<int, int>PII;
int n, m;
vector<PII>edges[N];
bool st[N];
void dfs(int u)
{
cout << u << endl;
st[u] = true;
for (auto t : edges[u])
{
int v = t.first; int w = t.second;
if (!st[v])
{
dfs(v);
}
}
}
void bfs(int u)
{
queue<int>q;
q.push(u);
st[u] = true;
while (q.size())
{
int a = q.front(); q.pop();
cout << a << endl;
for (auto t : edges[a])
{
int b = t.first; int c = t.second;
if (!st[b])
{
q.push(b);
st[b] = true;
}
}
}
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
int a, b, c; cin >> a >> b >> c;
edges[a].push_back({ b,c });
//如果是无向图的话,需要反存
edges[b].push_back({ a,c });
}
}3.链式前向星
const int N = 1e5 + 10;
int h[N], e[2 * N], w[2 * N], ne[2 * N], id;
//h[a]存储与a节点相连的最后一个下标 e[id]存储第id个 另一个端点b
//w[id]存储第id个权值 ne[id]存储上一个下标
int n, m;
void add(int a, int b, int c)
{
id++;
e[id] = b;
w[id] = c;
ne[id] = h[a];
h[a] = id;
}
bool st[N];
void dfs(int u)
{
cout << u << endl;
st[u] = true;
for (int i = h[u]; i; i = ne[i])//i先被赋值为最后一个与u相连的节点的下标,i不为0,i更新为上一个节点下标
{
int v = e[i];
if (!st[v])
{
dfs(v);
}
}
}
void bfs(int u)
{
queue<int>q;
q.push(u);
st[u] = true;
while (q.size())
{
int a = q.front(); q.pop();
cout << a << endl;
for (int i = ne[a]; i; i = ne[i])
{
int b = e[i]; int c = w[i];
if (!st[b])
{
q.push(b);
st[b] = true;
}
}
}
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= m; i++)
{
int a, b, c; cin >> a >> b >> c;
add(a, b, c);
//无向图反存
add(b, a, c);
}
}最小生成树:
一个具有n个顶点的连通图,其生成树为包含n-1条边和所有顶点的极小连通子图。对于生成树来说,若砍去一条边就会使得图不连通;若增加一条就会形成回路。
Prim算法:O(n^2+m)
核心:不断加点。
Prim 算法构造最小生成树的基本思想:
1. 从任意一个点开始构造最小生成树;
2. 将距离该树权值最小且不在树中的顶点,加入到生成树中。然后更新与该点相连的点到生成树的最短距离;
3. 重复操作n次,直到所有顶点都加入为止。
prim流程-->n次(找最小值--☑判断是否联通☑--最小值入树--更新最小值)
邻接矩阵--代码实现:
最小生成树【模板】(下述为两种实现代码)
1.邻接矩阵实现
const int N = 5010; //https://www.luogu.com.cn/problem/P3366
int edges[N][N];
int n, m;
bool st[N];//标记某个点到生成树的最短距离
int dist[N];//标记某个点是否加入生成树
int prim()
{
memset(dist, 0x3f, sizeof dist);
int ret = 0;
dist[1] = 0;//葱节点1开始造树
for (int i = 1; i <= n; i++)//循环加入n个点
{
int t = 0;//用t来标记最短距离点的下标
for (int j = 1; j <= n; j++)//遍历找最小值
{
if (!st[j] && dist[j] < dist[t])
t = j;
}
//判断是否联通
if (dist[t] == 0x3f3f3f3f)return 0x3f3f3f3f;
st[t] = true;
ret += dist[t];
//更新最短路径
for (int j = 1; j <= n; j++)
{
if (edges[t][j] < dist[j])dist[j] = edges[t][j];
}
}
return ret;
}
int main()
{
cin >> n >> m;
memset(edges, 0x3f, sizeof edges);//初始化
for (int i = 1; i <= m; i++)
{
int a, b, c; cin >> a >> b >> c;
edges[a][b] = min(edges[a][b], c); //重复路劲、环
edges[b][a] = min(edges[b][a], c);
}
int ret = 0;
ret = prim();
if (ret == 0x3f3f3f3f)cout << "orz" << endl;
else cout << ret << endl;
}vector数组--代码实现:
const int N = 5010,INF=0x3f3f3f3f;
typedef pair<int, int>PII;
vector<PII>edges[N];
int n, m;
int dist[N];
bool st[N];
int prim()
{
memset(dist, 0x3f, sizeof dist);
int ret = 0;
dist[1] = 0;
for (int i = 1; i <= n; i++)//n个顶点入树
{
int t = 0;
for (int j = 1; j <= n; j++)
{
if (!st[j] && dist[t] > dist[j])
t = j;
}
if (dist[t] == INF)return INF;//判断是否不联通
st[t] = true;
ret += dist[t];
for (auto x : edges[t])
{
int b = x.first; int c = x.second;
if (dist[b] > c)dist[b] = c;
}
}
return ret;
}
int main()
{
cin >> n >> m;
//memset(edges, 0x3f, sizeof edges); //vector数组不需要,因为后续 获取边时均合法
for (int i = 1; i <= m; i++)
{
int a, b, c; cin >> a >> b >> c;
edges[a].push_back({ b,c });//此处不用重边取小,prim算法会自动取小
edges[b].push_back({ a,c });
}
int ret = prim();
if (ret == INF)cout << "orz" << endl;
else cout << ret << endl;
}Kruskal算法:O(mlog m)
核心:不断加边
1. 所有边按照权值排序;
2. 每次选出权值最⼩且两端顶点不连通的⼀条边,直到所有顶点都联通。
Kruskal流程:初始化--进行边操作--☑判断是否联通☑
const int N = 5010,M=2e5+10,INF=0x3f3f3f3f;
int fa[N];//并查集
int n, m;
struct node
{
int a, b, c;
}a[M]; //m组
int find(int x)
{
if (x == fa[x])return x;
return fa[x] = find(fa[x]);
//return fa[x]==x?x:fa[x]=find(fa[x]);
}
int cmp(node& a, node& b)
{
return a.c < b.c;
}
int kk()
{
sort(a + 1, a + m + 1, cmp);//对边的权值进行排序
int ret = 0;
int cnt = 0;//对边进行计数,用于判断是否联通
for (int i = 1; i <= m; i++)
{
int x = a[i].a; int y = a[i].b; int c = a[i].c;
int fx = find(x); int fy = find(y);
if (fx != fy)
{
cnt++;
ret += c;
fa[fx] = fy;
}
}
return cnt == n - 1?ret : INF;//此处是判断是否联通
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)fa[i] = i;
for (int i = 1; i <= m; i++)
{
cin >> a[i].a >> a[i].b >> a[i].c;
}
int ret = kk();
if (ret == INF)cout << "orz" << endl;
else cout << ret << endl;
}练习部分:
(一般以Kruskal算法为主,因为并查集较为熟悉,当mlogm明显大于n^2时使用Prim算法)
1.
Kruskal算法:
const int N = 510;
int v, n;
int fa[N];//n个节点的关系
struct node
{
int a, b, c;
}a[N*N];
bool cmp(node& a, node& b)
{
return a.c < b.c;
}
int find(int x)
{
return fa[x] == x ? x : fa[x] = find(fa[x]);
}
int kk()
{
sort(a + 1, a + n * n + 1, cmp);
int ret = 0;
int cnt = 0;
for (int i = 1; i <= n * n; i++)
{
int x = a[i].a; int y = a[i].b; int c = a[i].c;
int fx = find(x); int fy = find(y);
if (fx != fy)
{
ret += c;
cnt++;
fa[fx] = fy;
}
if(cnt==n-1) return ret;
}
}
int main()
{
cin >> v >> n;
for (int i = 1; i <= n * n; i++)fa[i] = i;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
int tmp; cin >> tmp;
int sum = (i - 1) * n + j;
a[sum].a = i;
a[sum].b = j;
a[sum].c = v;//全部先初始化为最初标价v
if(i!=j&&tmp!=0)a[sum].c = min(tmp, a[sum].c);//tmp只有在不为0时更新
}
}
int ret = kk();
cout << ret + v << endl;//路径和加上最初一个点的价格v
}Prim算法:
const int N = 510;
int edges[N][N];
int v, n;
int dist[N];
bool st[N];
int prim()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
int ret = v; //初始化时直接计入第一个点的价值
for (int i = 1; i <= n; i++)//n个点入树
{
int t = 0;
//找最小权值
for (int j = 1; j <= n; j++)
{
if (!st[j] && dist[j] < dist[t])
t = j;
}
ret += dist[t];
st[t] = true;
//此题不用判断是否联通
//更新最短路径
for (int j = 1; j <= n; j++)
{
dist[j] = min(dist[j], edges[t][j]);
}
}
return ret;
}
int main()
{
cin >> v >> n;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
edges[i][j] = v;int tmp; cin >> tmp;
if (i != j && tmp != 0)edges[i][j] = min(edges[i][j], tmp);
}
}
int ret = prim();
cout << ret << endl;
}
prim流程-->n次(找最小值--判断是否联通--最小值入树--更新最小值)
2.
//Kruskal算法
const int N = 310, M = 8010;
int n, m;
struct node
{
int a, b, c;
}a[M];
int fa[N];//n个节点的关系
int find(int x)
{
return fa[x] == x ? x : fa[x] = find(fa[x]);
}
bool cmp(node& a, node& b)
{
return a.c < b.c;
}
int kk()
{
//初始化
for (int i = 1; i <= n; i++)fa[i] = i;
sort(a + 1, a + m + 1, cmp);
int ret = 0;//此处记得是max
for (int i = 1; i <= m; i++)
{
int x = a[i].a; int y = a[i].b; int c = a[i].c;
int fx = find(x), fy = find(y);
if (fx != fy)
{
ret = max(c, ret);
fa[fx] = fy;
}
}
//判断联通--此题不需要
return ret;
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= m; i++)cin >> a[i].a >> a[i].b >> a[i].c;
int ret = kk();
cout << n - 1 << " "<<ret<<endl;
return 0;
}
//Prim算法
#include<iostream>
#include<cstring>
#include<vector>
const int N = 310, M = 8010, INF = 0x3f3f3f3f;
typedef pair<int, int>PII;
int n, m;
vector<PII>edges[N];
int ret=0;
int dist[N];//存的是每个点到树的最短距离
bool st[N];
void Prim()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 1; i <= n; i++)//n个点入树
{
int t = 0;
for (int j = 1; j <= n; j++)//遍历找最小值
{
if (!st[j] && dist[j] < dist[t])
t = j;
}
//判断连通性---此题不需要
//if (dist[t] == INF)return INF;
//点入树
ret = max(ret, dist[t]);
st[t] = true;
//更新最小值
for (auto x:edges[t])
{
int b = x.first; int c = x.second;
dist[b] = min(dist[b], c);
}
}
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= m; i++)
{
int a, b, c; cin >> a >> b >> c;
edges[a].push_back({ b,c });
edges[b].push_back({ a,c });
}
Prim();
cout << n - 1 << " " << ret << endl;
return 0;
}3.直接来一道省选题(与前两题的差别是,此题为有向图)
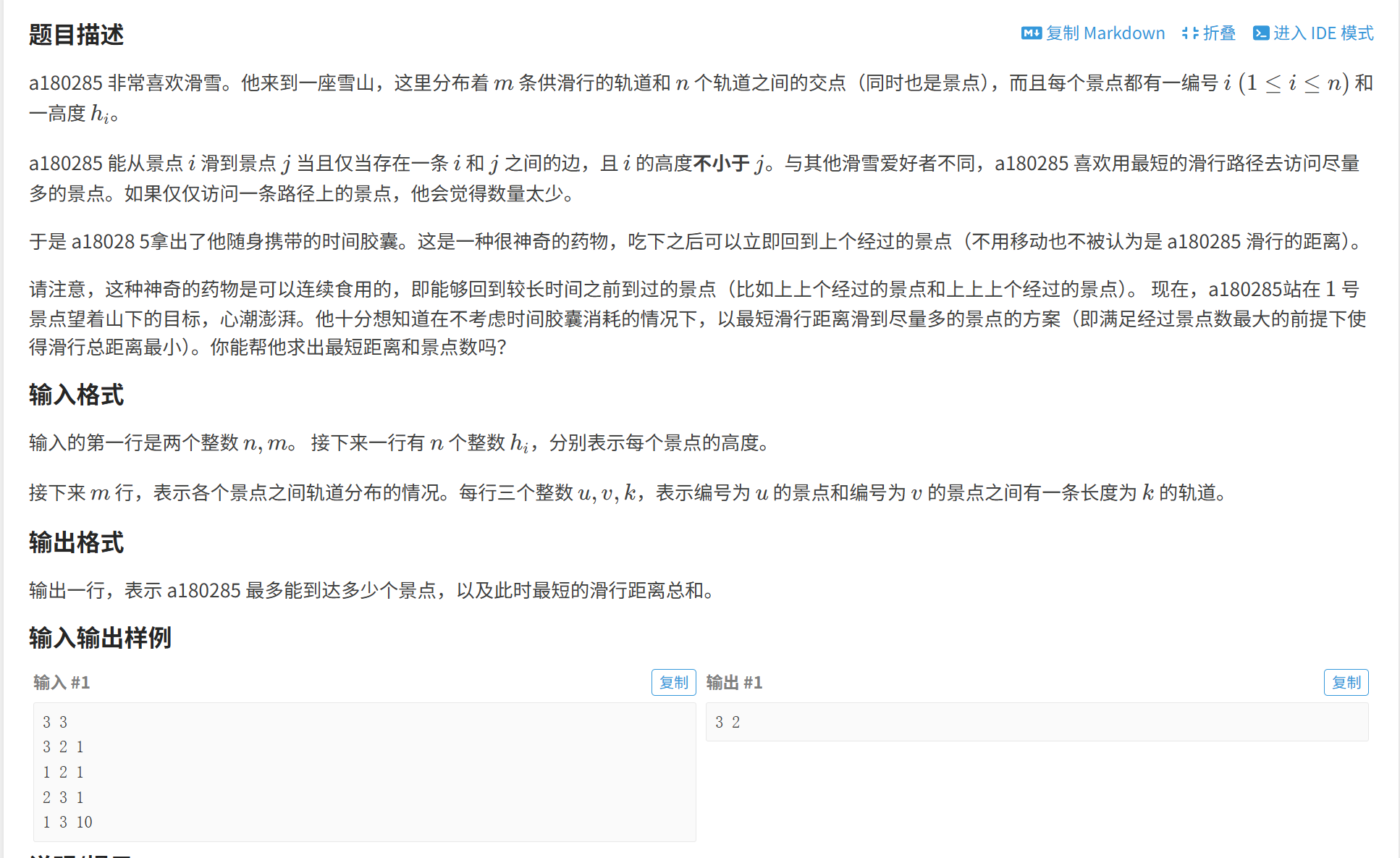
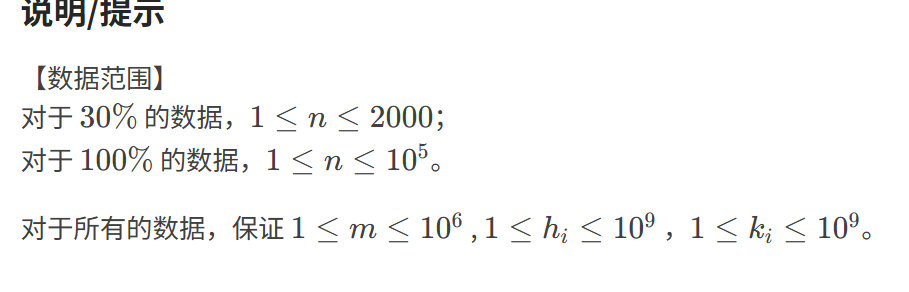
此题首先问的是最多可以到达多少个点,使用dfs,bfs均可解决。(顺带将1号点向外衍生的边全部存储)
第二问是在第一问的基础上求最短路径(从1号点开始),由数据范围可知不能用Prim算法(n^2-->1e10会导致超时),应该使用Kruskal算法,但是sort排序时不能只按照权值大小,此处排序的核心是先按照另一点b的高度,在点的高度b1,b2相同时再按照权值大小排序。
typedef long long LL;
typedef pair<int, int>PII;
const int N = 1e5 + 10, M = 1e6 + 10;
LL ret;
int h[N];
int fa[N];
int n, m, cnt;
vector<PII>edges[N];
int pos = 0;
int find(int x)
{
return fa[x] == x ? x : fa[x] = find(fa[x]);
}
struct node
{
int a, b, c;
}e[M];
bool st[N];//标记DFS中哪些点已经遍历过
void dfs(int i)
{
cnt++;
st[i] = true;
for (auto x : edges[i])
{
int a = i, b = x.first, c = x.second;
e[++pos].a = a; e[pos].b = x.first; e[pos].c = x.second;
if (!st[b])dfs(b);
}
}
bool cmp(node& x, node& y) //根据题意,先考虑高度,再考虑路径长度
{
int a1 = x.a, b1 = x.b, c1 = x.c;
int a2 = y.a, b2 = y.b, c2 = y.c;
if (h[b1] != h[b2])return h[b1] > h[b2];
else return c1<c2;
}
void kk()
{
for (int i = 1; i <= n; i++)fa[i] = i;
sort(e + 1, e + pos + 1, cmp);
for (int i = 1; i <= pos; i++)
{
int x = e[i].a, y = e[i].b, c = e[i].c;
int fx = find(x), fy = find(y);
if (fx != fy)
{
ret += c;
fa[fx] = fy;
}
}
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)cin >> h[i];
for (int i = 1; i <= m; i++)
{
int a, b, c; cin >> a >> b >> c;
if (h[a] > h[b])edges[a].push_back({ b,c });
else if (h[a] == h[b])
{
edges[a].push_back({ b,c });
edges[b].push_back({ a,c });
}
else edges[b].push_back({ a,c });
}
dfs(1);
kk();
cout << cnt << " " << ret << endl;
}






















 8517
8517


 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?







