C++进阶-封装红黑树模拟实现map和set（难度较高）

最新推荐文章于 2025-08-04 19:56:00 发布
最新推荐文章于 2025-08-04 19:56:00 发布
阅读量1k 收藏 18
点赞数 13
CC 4.0 BY-SA版权
分类专栏： C++篇 文章标签： c++ 开发语言
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/2401_86446710/article/details/149877888

目录

1.预备知识

2.初步代码

3.对红黑树实现的代码进行改造

4.对map和set的改造

5.对RBTree::insert的改造

6.对RBTree::Find函数的改造

7.实现iterator(最重要)

8.实现const_iterator

9.完成set和map的key不能修改

10.实现map的operator[]

11.代码汇总

12.总结


1.预备知识

我们要了解一下map和set这两个容器，可以到C++官网中搜索map和set进行了解，以下是C++官网链接：

Reference - C++ Reference

如果想了解更多，可以去看我写的两篇关于map和set的博客：

C++进阶-set-优快云博客文章浏览阅读608次，点赞23次，收藏17次。本文系统介绍了C++ STL中的set容器的特性与使用方法。set作为关联式容器，基于红黑树实现，具有自动去重和排序功能，增删查效率为O(logN)。文章详细讲解了set的构造函数、常用成员函数（如emplace_hint、key_comp等）以及边界查找函数（lower_bound、upper_bound等），并通过代码示例演示了其具体用法。同时对比了set与multiset的差异，指出后者允许重复元素。最后通过两个力扣编程题（查找数组交集和环形链表入口）展示了set的实际应用场景，体现了其在数据去重和快 https://blog.youkuaiyun.com/2401_86446710/article/details/149322360?spm=1011.2415.3001.10575&sharefrom=mp_manage_linkC++进阶-map-优快云博客文章浏览阅读835次，点赞26次，收藏14次。本文介绍了C++ STL中的map容器。map是基于二叉搜索树实现的键值对容器，具有自动排序特性。文章详细讲解了map的声明方式、构造函数、operator[]操作符（可查找/插入元素）、at方法（安全访问）、emplace_hint高效插入等核心功能。特别强调了map与set的区别在于存储键值对，以及operator[]的独特行为（找不到键时会自动插入）。还介绍了辅助类pair的用法，以及key_comp/value_comp比较函数的使用。通过多个代码示例演示了map的基本操作，包括元素访问、修改和异常 https://blog.youkuaiyun.com/2401_86446710/article/details/149344636?spm=1011.2415.3001.10575&sharefrom=mp_manage_link非常建议去了解一下C++的红黑树的内容，以方便我们实现map和set：

C++进阶-红黑树（难度较高）-优快云博客文章浏览阅读1.7k次，点赞52次，收藏56次。本文详细讲解了红黑树的实现原理和代码实现。主要内容包括： 红黑树的基本概念和五大规则，确保最长路径不超过最短路径的两倍； 红黑树的插入操作，重点分析了不同情况下的变色和旋转处理（单旋、双旋）； 完整代码实现，包括结点定义、旋转操作、插入逻辑和验证方法； 红黑树查找的实现和测试用例； 简要介绍了删除操作的思路。 红黑树通过颜色约束和旋转操作保持近似平衡，效率与AVL树相当但旋转次数更少。本文强调理解旋转逻辑的重要性，建议通过画图辅助理解。代码经过测试验证，为后续用红黑树实现map和set打下基础。 https://blog.youkuaiyun.com/2401_86446710/article/details/149436642?spm=1011.2415.3001.10575&sharefrom=mp_manage_link

map和set的iterator和list差不多，建议各位参考一下list的模拟实现，可以见以下博客：

C++初阶-list的模拟实现（难度较高）-优快云博客文章浏览阅读916次，点赞27次，收藏24次。这篇文章详细讲解了C++中list容器的模拟实现过程。主要内容包括：1) list基本结构的定义，使用双向链表实现；2) 无参构造函数和节点构造函数的实现；3) push_back等基本操作的实现；4) 迭代器类的设计与实现，包括普通迭代器和const迭代器；5) list类迭代器相关函数的实现；6) 增删查改等操作的实现；7) 拷贝控制成员函数和特殊成员函数的实现；8) 测试用例的编写。文章通过代码示例详细展示了list容器的底层实现原理，包括哨兵位的使用、迭代器封装等技术细节，并提供了完整的测试代码验证 https://blog.youkuaiyun.com/2401_86446710/article/details/148548215?spm=1011.2415.3001.10575&sharefrom=mp_manage_link

2.初步代码

该代码是实现红黑树的实现时，去掉注释后的代码：

#define _CRT_SECURE_NO_WARNINGS 1
#include <assert.h>
#include<vector>
#include<iostream>
using namespace std;
enum Color
{
	Red,
	Black
};
template<class K,class V>
struct RBTreeNode
{
	pair<K, V> _kv;
	RBTreeNode<K, V>* _parent;
	RBTreeNode<K, V>* _left;
	RBTreeNode<K, V>* _right;
	Color _col;
	RBTreeNode(const pair<K,V>& kv)
		:_kv(kv)
		,_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
	{ }
};
template<class K,class V>
class RBTree
{
	typedef RBTreeNode<K, V> Node;
public:
	void RotateR(Node* parent)
	{
		assert(parent != nullptr);
		Node* subL = parent->_left;
		assert(subL != nullptr);
		Node* subLR = subL->_right;
		parent->_left = subLR;
		subL->_right = parent;
		if (subLR)
		{
			subLR->_parent = parent;
		}
		Node* parentParent = parent->_parent;
		parent->_parent = subL;
		if (parent == _root)
		{
			subL->_parent = nullptr;
			_root = subL;
		}
		else
		{
			if (parentParent->_left == parent)
			{
				parentParent->_left = subL;
			}
			else
			{
				parentParent->_right = subL;
			}
			subL->_parent = parentParent;
		}
	}
	void RotateL(Node* parent)
	{
		assert(parent != nullptr);
		Node* subR = parent->_right;
		assert(subR != nullptr);
		Node* subRL = subR->_left;
		parent->_right = subRL;
		if (subRL)
		{
			subRL->_parent = parent;
		}
		subR->_left = parent;
		Node* parentParent = parent->_parent;
		parent->_parent = subR;
		if (parent == _root)
		{
			subR->_parent = nullptr;
			_root = subR;
		}
		else
		{
			if (parentParent->_left == parent)
			{
				parentParent->_left = subR;
			}
			else
			{
				parentParent->_right = subR;
			}
			subR->_parent = parentParent;
		}
	}
	bool Insert(const pair<K, V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);
			_root->_col = Black;
			return true;
		}
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return false;
			}
		}
		cur = new Node(kv);
		cur->_parent = parent;
		if (parent->_kv.first > kv.first)
		{
			parent->_left = cur;
		}
		else
		{
			parent->_right = cur;
		}
		cur->_col = Red;
		while (parent && parent->_col == Red)
		{
			Node* grandfather = parent->_parent;
			if (grandfather->_left == parent)
			{
				Node* uncle = grandfather->_right;
				if (uncle && uncle->_col == Red)
				{
					uncle->_col = parent->_col = Black;
					grandfather->_col = Red;
					cur = grandfather;
					parent = cur->_parent;
				}
				else
				{
					if (parent->_left == cur)
					{
						RotateR(grandfather);
						parent->_col = Black;
						grandfather->_col = Red;
					}
					else
					{
						RotateL(parent);
						RotateR(grandfather);
						cur->_col = Black;
						grandfather->_col = Red;
					}
					break;
				}
			}
			else
			{
				Node* uncle = grandfather->_left;
				if (uncle && uncle->_col == Red)
				{
					uncle->_col = parent->_col = Black;
					grandfather->_col = Red;
					cur = grandfather;
					parent = cur->_parent;
				}
				else
				{
					if (parent->_right == cur)
					{
						parent->_col = Black;
						grandfather->_col = Red;
					}
					else
					{
						RotateR(parent);
						RotateL(grandfather);
						grandfather->_col = Red;
						cur->_col = Black;
					}
					break;
				}
			}
		}
		_root->_col = Black;
		return true;
	}
	Node* Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first < key)
			{
				cur = cur->_right;
			}
			else if (cur->_kv.first > key)
			{
				cur = cur->_left;
			}
			else
			{
				return cur;
			}
		}
		return nullptr;
	}
	bool Check(Node* root, int blackNum, const int refNum)
	{
		if (root == nullptr)
		{
			if (refNum != blackNum)
			{
				cout << "存在⿊⾊结点的数量不相等的路径" << endl;
				return false;
			}
			return true;
		}
		if (root->_col == Red && root->_parent->_col == Red)
		{
			cout << root->_kv.first << "存在连续的红⾊结点" << endl;
			return false;
		}
		if (root->_col == Black)
		{
			blackNum++;
		}
		return Check(root->_left, blackNum, refNum)
			&& Check(root->_right, blackNum, refNum);
	}
	bool IsBalance()
	{
		if (_root == nullptr)
			return true;
		if (_root->_col == Red)
			return false;
		int refNum = 0;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_col == Black)
			{
				++refNum;
			}
			cur = cur->_left;
		}
		return Check(_root, 0, refNum);
	}
	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}
	void _InOrder(Node* root)
	{
		if (root == nullptr)
		{
			return;
		}
		_InOrder(root->_left);
		cout << root->_kv.first << " ";
		_InOrder(root->_right);
	}
private:
	Node* _root = nullptr;
};

以上代码将会放到RBTree.h文件中。

3.对红黑树实现的代码进行改造

改造红黑树代码是为了实现我们的set和map两个容器。

由于set是只存放了一个值，故我们要把红黑树的结点结构改成key结构：

template<class T>
struct RBTreeNode
{
	T _data;//存放数据，可以传递T为pair类型
	RBTreeNode<T>* _parent;
	RBTreeNode<T>* _left;
	RBTreeNode<T>* _right;
	Color _col;
	RBTreeNode(const T& data)
		:_data(data)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
	{
	}
};

我们还需要把RBTree.h中改一部分：

template<class K,class T>
class RBTree
{
public:
	typedef RBTreeNode<T> Node;
    bool Insert(const T& kv)
    {//……
    }
//……
};

Insert函数里面结构我们先不要改，之后再进行集中改变。

4.对map和set的改造

首先我们需要把map和set的基本结构写出来，这里map的模拟实现放到mymap.h中，set的模拟实现放到myset.h中：

//myset.h
#include"RBTree.h"
template<class K>
class myset
{
public:
    //以后代码增加的地方
	bool insert(const K& key)
	{
		return _t.Insert(key);
	}
private:
	RBTree<K, K> _t;
};

为了不破坏太多的RBTree结构，我们这里的set就构造成key-key结构，保持和set的源码的方式一样（源码各位可以自行搜索，如果想改造成一个参数的结构就把RBTree第二个模板参数置为缺省参数，缺省值为K）。

//mymap.h
#include"RBTree.h"
template<class K,class V>
class mymap
{
public:
    //以后代码增加的地方
	bool insert(const pair<K,V>& kv)
	{
		return _t.Insert(kv);
	}
private:
	RBTree<K, pair<K,V>> _t;
};

这样写的原因是：我们的RBTree的第二个模板参数是T，相当于我们的键值对，这样写主要是为了适应RBTree的insert函数。

5.对RBTree::insert的改造

改造该函数之前的代码：

bool Insert(const T& kv)
{
	if (_root == nullptr)
	{
		_root = new Node(kv);
		_root->_col = Black;
		return true;
	}
	Node* cur = _root;
	Node* parent = nullptr;
	while (cur)
	{
		if (cur->_kv.first > kv.first)
		{
			parent = cur;
			cur = cur->_left;
		}
		else if (cur->_kv.first < kv.first)
		{
			parent = cur;
			cur = cur->_right;
		}
		else
		{
			return false;
		}
	}
	cur = new Node(kv);
	cur->_parent = parent;
	if (parent->_kv.first > kv.first)
	{
		parent->_left = cur;
	}
	else
	{
		parent->_right = cur;
	}
	cur->_col = Red;
	while (parent && parent->_col == Red)
	{
		Node* grandfather = parent->_parent;
		if (grandfather->_left == parent)
		{
			Node* uncle = grandfather->_right;
			if (uncle && uncle->_col == Red)
			{
				uncle->_col = parent->_col = Black;
				grandfather->_col = Red;
				cur = grandfather;
				parent = cur->_parent;
			}
			else
			{
				if (parent->_left == cur)
				{
					RotateR(grandfather);
					parent->_col = Black;
					grandfather->_col = Red;
				}
				else
				{
					RotateL(parent);
					RotateR(grandfather);
					cur->_col = Black;
					grandfather->_col = Red;
				}
				break;
			}
		}
		else
		{
			Node* uncle = grandfather->_left;
			if (uncle && uncle->_col == Red)
			{
				uncle->_col = parent->_col = Black;
				grandfather->_col = Red;
				cur = grandfather;
				parent = cur->_parent;
			}
			else
			{
				if (parent->_right == cur)
				{
					parent->_col = Black;
					grandfather->_col = Red;
				}
				else
				{
					RotateR(parent);
					RotateL(grandfather);
					grandfather->_col = Red;
					cur->_col = Black;
				}
				break;
			}
		}
	}
	_root->_col = Black;
	return true;
}

由于参数改变，我们需要把_kv.first直接变成_data，所以有：

bool Insert(const T& data)
{
	if (_root == nullptr)
	{
		_root = new Node(data);
		_root->_col = Black;
		return true;
	}
	Node* cur = _root;
	Node* parent = nullptr;
	while (cur)
	{
		if (cur->_data > data)
		{
			parent = cur;
			cur = cur->_left;
		}
		else if (cur->_data < data)
		{
			parent = cur;
			cur = cur->_right;
		}
		else
		{
			return false;
		}
	}
	cur = new Node(data);
	cur->_parent = parent;
	if (parent->_data > data)
	{
		parent->_left = cur;
	}
	else
	{
		parent->_right = cur;
	}
	cur->_col = Red;
	while (parent && parent->_col == Red)
	{
		Node* grandfather = parent->_parent;
		if (grandfather->_left == parent)
		{
			Node* uncle = grandfather->_right;
			if (uncle && uncle->_col == Red)
			{
				uncle->_col = parent->_col = Black;
				grandfather->_col = Red;
				cur = grandfather;
				parent = cur->_parent;
			}
			else
			{
				if (parent->_left == cur)
				{
					RotateR(grandfather);
					parent->_col = Black;
					grandfather->_col = Red;
				}
				else
				{
					RotateL(parent);
					RotateR(grandfather);
					cur->_col = Black;
					grandfather->_col = Red;
				}
				break;
			}
		}
		else
		{
			Node* uncle = grandfather->_left;
			if (uncle && uncle->_col == Red)
			{
				uncle->_col = parent->_col = Black;
				grandfather->_col = Red;
				cur = grandfather;
				parent = cur->_parent;
			}
			else
			{
				if (parent->_right == cur)
				{
					parent->_col = Black;
					grandfather->_col = Red;
				}
				else
				{
					RotateR(parent);
					RotateL(grandfather);
					grandfather->_col = Red;
					cur->_col = Black;
				}
				break;
			}
		}
	}
	_root->_col = Black;
	return true;
}

这里主要是要注意一下：如果我们是插入一个键值对即pair类型时，如果我们直接用parent->_data<data能不能比较出正确的结果，实际上，我们在C++官网中也很容易得到结论：

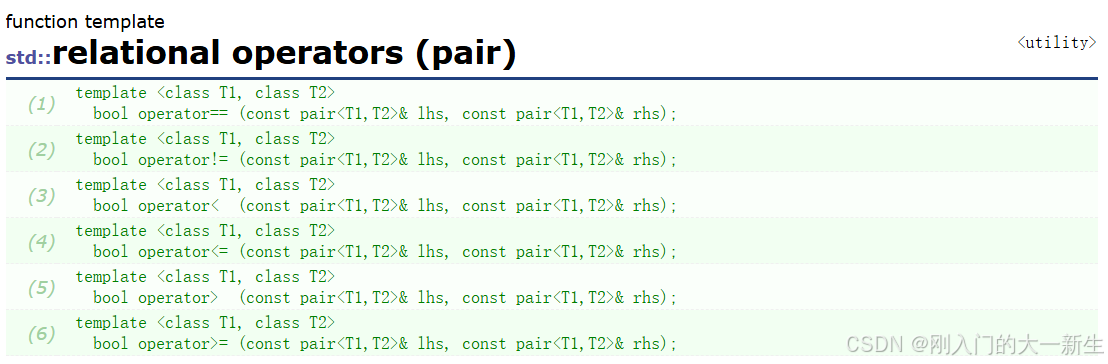
但是我们就想要只用first进行比较，所以我们不能直接这样写。

如果我们使用仿函数来进行比较逻辑，那么在这个时候也是不行的，因为如果用仿函数的话，我们要Find，而Find是用key来比较的，如果用仿函数，我们如何取得map的key值从而使比较逻辑正确？

实际上，我们可以用仿函数进行，但是这个仿函数不能单单用来比较大小，还要取得key，这个时候，我们可以这样写：

//RBTree.h
template<class K,class T,class KeyOfT>
class RBTree
{};

通过给RBTree增加一个模板参数来接收仿函数进行比较的逻辑，同时要改：

//myset.h
template<class K>
class myset
{
	struct SetKeyOfT
	{
		const K& operator()(const K& key)
		{
			return key;
		}
	};
private:
	RBTree<K, K, SetKeyOfT> _t;
};
//mymap.h
template<class K,class V>
class mymap
{
	struct MapKeyOfT
	{
		const K& operator()(const pair<K, V>& kv)
		{
			return kv.first;
		}
	};
private:
	RBTree<K, pair<K, V>, MapKeyOfT> _t;
};

同时，我们还需要把比较逻辑改成二者key的比较，所以可以这样写：

	bool Insert(const T& data)
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);
			_root->_col = Black;
			return true;
		}
		KeyOfT kot;
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			if (kot(cur->_data) > kot(data))
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (kot(cur->_data) < kot(data))
		    {
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return false;
			}
		}
		cur = new Node(data);
		cur->_parent = parent;
		if (kot(parent->_data) > kot(data))
		{
			parent->_left = cur;
		}
		else
		{
			parent->_right = cur;
		}
//……
}

6.对RBTree::Find函数的改造

和insert函数类似，我们也可以对Find函数进行改造：

//RBTree.h
bool Find(const K& key)
{
	KeyOfT kot;
	Node* cur = _root;
	while (cur)
	{
		if (kot(cur->_data) < key)
		{
			cur = cur->_right;
		}
		else if (kot(cur->_data) > key)
		{
			cur = cur->_left;
		}
		else
		{
			return true;
		}
	}
	return false;
}

7.实现iterator(最重要)

实现iterator的思路：

（1）iterator实现的⼤框架跟list的iterator思路是⼀致的，⽤⼀个类型封装结点的指针，再通过重载运算符实现，迭代器像指针⼀样访问的⾏为。

这里我先把iterator基本结构写出来：

//RBTree.h
template<class T>
struct _TreeIterator
{
	typedef RBTreeNode<T> Node;
	typedef _TreeIterator<T> Self;
	Node* _node;
	_TreeIterator(Node* node)
		:_node(node)
	{ }
	T& operator*()
	{
		return _node->_data;
	}
	T* operator->()
	{
		return &_node->_data;
	}
	bool operator!=(const Self& s)
	{
		return _node!=s._node;
	}
};

我们这里主要要理解一下如何实现operator++和operator--。

首先map和set走的是中序遍历，所以返回的第一个结点的iterator是begin()。

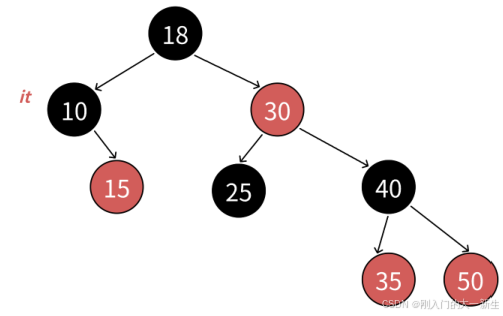
第一个结点就是10这个结点，也就是说我们需要从根结点开始走起，一直往左子树遍历，直到左子树为空时。

（2）迭代器++的核⼼逻辑就是不看全局，只看局部，只考虑当前中序局部要访问的下⼀个结点。

我们不用管其他结点，就看这个子树，如果这棵子树遍历到左孩子，就看根；如果遍历到根，就看右孩子。

（3）迭代器++时，如果it指向的结点的右⼦树不为空，代表当前结点已经访问完了，要访问下⼀个结点是右⼦树的中序第⼀个，⼀棵树中序第⼀个是最左结点，所以直接找右⼦树的最左结点即可。

（4）迭代器++时，如果it指向的结点的右⼦树空，代表当前结点已经访问完了且当前结点所在的⼦树也访问完了，要访问的下⼀个结点在当前结点的祖先⾥⾯，所以要沿着当前结点到根的祖先路径向上找。

（5）如果当前结点是⽗亲的左，根据中序左⼦树->根结点->右⼦树，那么下⼀个访问的结点就是当前结点的⽗亲；

（6）如果当前结点是⽗亲的右，根据中序左⼦树->根结点->右⼦树，当前结点所在的⼦树访问完了，当前结点所在⽗亲的⼦树也访问完了，那么下⼀个访问的需要继续往根的祖先中去找，直到找到孩⼦是⽗亲左的那个祖先就是中序要访问的下⼀个结点。

这上面都是有些难以理解的，我这里就直接用画图的方式加以讲解：

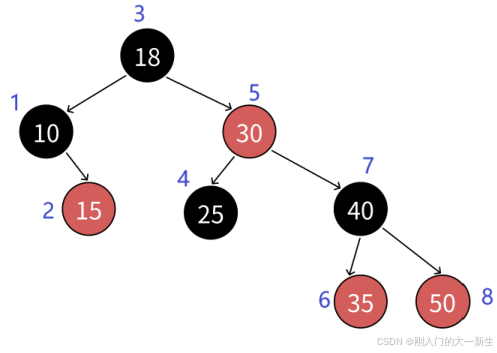
我按照中序遍历的顺序进行讲解。

首先从根结点开始往左子树遍历，发现18的左孩子不为空，则10作为左子树的根结点继续遍历，然后发现10没有左孩子，这个时候就遍历到10这个结点。

遍历到10结点后，++，我们发现10为根结点，所以要继续遍历右子树，遍历到15结点，发现15结点没有左孩子，所以直接返回到15这个结点。

遍历到15结点后，++，我们发现15结点没有右子树，所以往上递归，然后发现10为18的左孩子，所以是一定遍历过的，所以就继续往上；发现18是根结点，这个时候就返回18这个结点了。

遍历到18结点后，++，发现30为右孩子，而且30还有左孩子，所以遍历到25，发现25没有左孩子，所以返回25。

遍历到25结点后，++，发现25没有右孩子，所以返回到25的父亲，到30结点，返回30。

遍历到30结点后，………………

直到到达50结点（已经被访问过），如果++，发现没有右孩子，然后往上，发现父亲都为爷爷的右孩子，证明该子树遍历完，所以继续往上访问，直到没有父亲或者该孩子为父亲的左结点为止。这个时候我们发现父亲为空，则这个时候返回nullptr，所以这个时候直接就是用nullptr构造一个结点进行返回。

//_TreeIterator
Self& operator++()
{
	//中序遍历，这个时候就需要访问右孩子
	if (_node->_right)
	{
		//找右子树的最左结点
		_node = _node->_right;
		while (_node->_left)
		{
			_node = _node->_left;
		}
	}
	else
	{
		//右子树为空
		//对应15结点或者50结点
		Node* cur = _node;
		Node* parent = cur->_parent;
		//当parent不为空，且cur为parent的右孩子是继续往上
		//因为这代表该子树已经遍历完了
		while (parent && cur == parent->_right)
		{
			cur = parent;
			parent = cur->_parent;
		}
		//要么cur是parent的左孩子，这个时候就可以直接用_node=parent
		//这两种情况都可以这样写
		_node = parent;
	}
	return *this;
}

以上逻辑需要结合画图理解，最重要的是我们要理解为什么当右孩子没有时要往上递归，因为这个时候该子树都遍历完了（如：15结点，为10的右孩子，根据左根右的遍历方式，右孩子都被遍历完了，那么也就代表根也被遍历完了，所以我们需要往上，此外，如果cur（当前结点）是父亲的左孩子，代表父亲（根）还没有被遍历，所以直接用父亲作为结点返回）。

相似的逻辑我们还可以写出--，其逻辑和++完全相反，不过还有特殊处理一下当_node==nullptr的情况，这个时候就是end()，我们需要得到root以遍历子树：

//_TreeIterator
Node* _root;
_TreeIterator(Node* node,Node* root)
	:_node(node)
	,_root(root)
{ }
Self& operator--()
{
	if (_node == nullptr) // end()
	{
		// --end()，特殊处理，⾛到中序最后⼀个结点，整棵树的最右结点
		Node* rightMost = _root;
		while (rightMost && rightMost->_right)
		{
			rightMost = rightMost->_right;
		}
		_node = rightMost;
	}
	else if (_node->_left)
	{
		//代表该子树还没遍历完
		//找左子树的最右结点
		_node = _node->_left;
		while (_node->_right)
		{
			_node = _node->_right;
		}
	}
	else
	{
		//该子树被遍历完
		//向上查找，直到查找到根或者该孩子为父亲的右孩子
		Node* cur = _node;
		Node* parent = cur->_parent;
		while (parent && cur == parent->_left)
		{
			cur = parent;
			parent = cur->_parent;
		}
		_node = parent;
	}
	return *this;
}

我们的目的是为了得到Bgein和End，所以在RBTree中加：

//RBTree
public:
typedef _TreeIterator<T> Iterator;
Iterator Begin()
{
	Node* minleft = _root;
	while (minleft && minleft->_left)
	{
		minleft = minleft->_left;
	}
	//调用_TreeIterator
	//相当于_TreeIterator(minleft)
	return Iterator(minleft, _root);
}
Iterator End()
{
	return Iterator(nullptr, _root);
}

同样，我们还需要在mymap和myset中进行修改：

//myset
public:
typedef RBTree<K, K, SetKeyOfT>::Iterator iterator;
iterator begin()
{
	return _t.Begin();
}
iterator end()
{
	return _t.End();
}
//mymap
public:
typedef RBTree<K, pair<K, V>, MapKeyOfT>::Iterator iterator;
iterator begin()
{
	return _t.Begin();
}
iterator end()
{
	return _t.End();
}

这个时候要注意：我们现在在测试文件中随便写一个主函数都会报错：

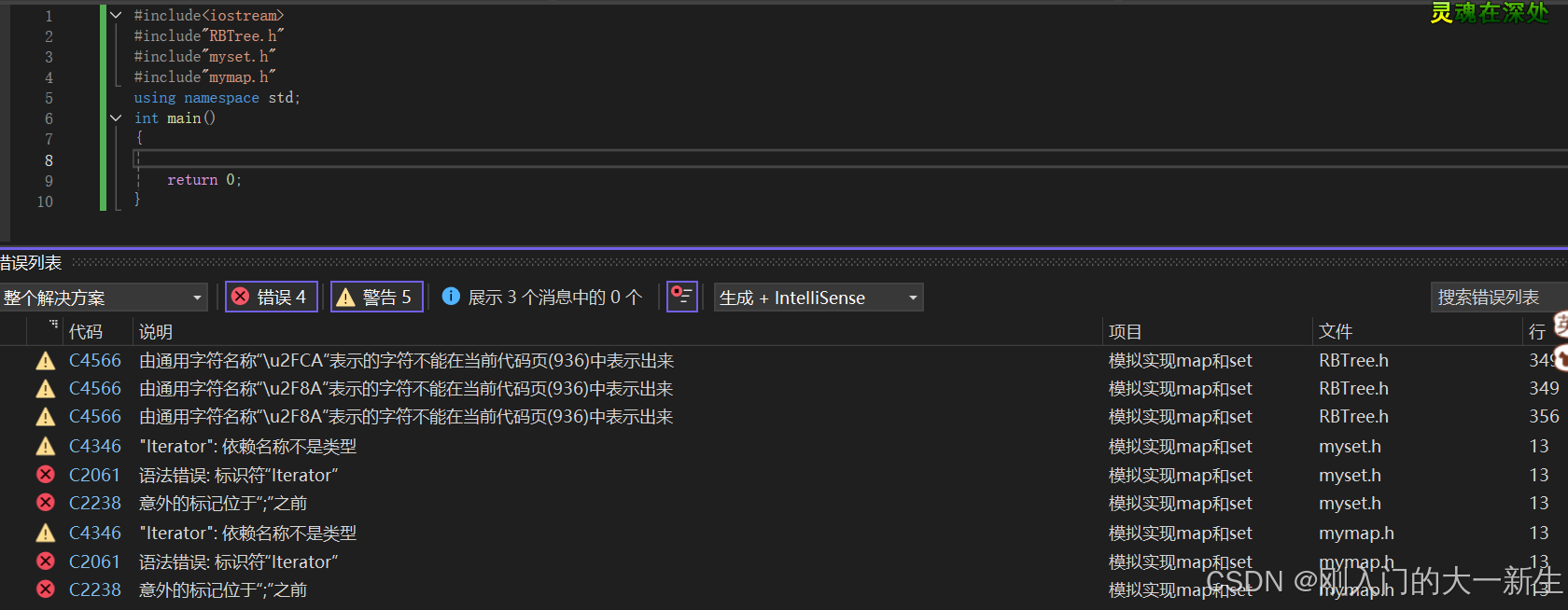
这主要是因为：如果我们要取模板里面的类型（含内嵌类型、内部类）都要加typename，因为取模板里的东西，现在的模板可能还没有实例化，此时取的模板里面的类型编译器分不清楚它是静态成员变量还是内嵌类型，而我们这样写：

typedef typename RBTree<K, K, SetKeyOfT>::Iterator iterator;
typedef typename RBTree<K, pair<K, V>, MapKeyOfT>::Iterator iterator;

那个typename就是告诉编译器这是一个类型，是合乎语法的，而确定这个类型要等到类模板被实例化后就可以了，这样就没问题了。

不过我们也可以改造成这样也是没问题的：

using iterator = typename RBTree<K, K, SetKeyOfT>::Iterator;
using iterator = typename RBTree<K, pair<K, V>, MapKeyOfT>::Iterator;

这种写法更好一些，以后见到这种写法也不要奇怪。

以上是iterator基本的实现，不过如果你觉得可以再进行完善功能的话也可以，以下代码可以选择性加到_TreeIterator中：

//_TreeIterator
bool operator==(const Self& s)
{
	return _node == s._node;
}
//后置++
Self operator++(int)
{
	Self tmp = *this;  // 保存当前状态
	++(*this);         // 调用前置++实现
	return tmp;        // 返回旧值
}
//后置--
Self operator--(int)
{
	Self tmp = *this;  // 保存当前状态
	--(*this);         // 调用前置--实现
	return tmp;        // 返回旧值
}

8.实现const_iterator

和list一样，我们最好还是不要增加一个一样的类来实现const_iterator，可以在_TreeIterator模板参数后加两个模板参数，以下是_TreeIterator的改造：

//_TreeIterator
template<class T,class Ref,class Ptr>
struct _TreeIterator
{
typedef _TreeIterator<T, Ref, Ptr> Self;//Ref:引用，Ptr:指针
Ref operator*()
{
	return _node->_data;
}
Ptr operator->()
{
	return &_node->_data;
}
};

以下是对RBTree的改造：

template<class K,class T,class KeyOfT>
class RBTree
{
public:
typedef _TreeIterator<T, T&, T*> Iterator;
typedef _TreeIterator<T, const T&, const T*> ConstIterator;
ConstIterator Begin() const
{
	Node* minleft = _root;
	while (minleft && minleft->_left)
	{
		minleft = minleft->_left;
	}
	return ConstIterator(minleft, _root);
}
ConstIterator End() const
{
	return ConstIterator(nullptr, _root);
}
}；

同理，我们还需要在mymap和myset中进行改造：

//myset
public:
//下面两种随意选：
//typedef typename RBTree<K, K, SetKeyOfT>::ConstIterator const_iterator;
using const_iterator = typename RBTree<K, K, SetKeyOfT>::ConstIterator;
const_iterator begin() const
{
	return _t.Begin();
}
const_iterator end() const
{
	return _t.End();
}
//mymap
//下面两种随便选一种
//typedef typename RBTree<K, pair<K, V>, MapKeyOfT>::ConstIterator const_iterator;
using const_iterator = typename RBTree<K, pair<K, V>, MapKeyOfT>::ConstIterator;
const_iterator begin() const
{
	return _t.Begin();
}
const_iterator end() const
{
	return _t.End();
}

9.完成set和map的key不能修改

这个是改造代码比较少的部分，但是还是需要注意，我们不支持key修改不是代表value不支持修改，所以需要改造成这样：

//myset
public:
//下面两种随意选
//typedef typename RBTree<K,const K, SetKeyOfT>::Iterator iterator;
using iterator = typename RBTree<K, const K, SetKeyOfT>::Iterator;
//下面两种随意选
//typedef typename RBTree<K,const K, SetKeyOfT>::ConstIterator const_iterator;
using const_iterator = typename RBTree<K,const K, SetKeyOfT>::ConstIterator;
private:
    RBTree<K, const K, SetKeyOfT> _t;

需要注意的是RBTree的第二个参数才是所存储的东西，所以是第二个参数加const，第一个参数代表的是类型，第二个参数代表的是所存储的值。

类似，我们还可以对mymap进行改造：

//mymap
public:
//下面两种随便选一种
//typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::Iterator iterator;
using iterator = typename RBTree<K, pair<const K, V>, MapKeyOfT>::Iterator;
//下面两种随便选一种
//typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::ConstIterator const_iterator;
using const_iterator = typename RBTree<K, pair<const K, V>, MapKeyOfT>::ConstIterator;
private:
    RBTree<K, pair<const K, V>, MapKeyOfT> _t;

10.实现map的operator[]

首先，实际上，map的Insert函数返回值是pair<Iterator,bool>类型，map的operator[]会根据insert的返回值的bool来判断是否需要插入，当insert成功时，第一个参数是为新插入位置的结点地址，当insert失败时，第一个参数是为原结点的地址。

而这个时候operator[]就返回了该结点对应的值（value）。

所以关键是对Insert的改造，我们可以改造成这样：

//RBTree
pair<Iterator,bool> Insert(const T& data)
{
	if (_root == nullptr)
	{
		_root = new Node(data);
		_root->_col = Black;
		return { Iterator(_root,_root),true };//隐式类型转换
	}
	KeyOfT kot;
	Node* cur = _root;
	Node* parent = nullptr;
	while (cur)
	{
		if (kot(cur->_data) > kot(data))
		{
			parent = cur;
			cur = cur->_left;
		}
		else if (kot(cur->_data) < kot(data))
	    {
			parent = cur;
			cur = cur->_right;
		}
		else
		{
			return { Iterator(cur,_root),true };
		}
	}
	cur = new Node(data);
	Node* newnode = cur;
	cur->_parent = parent;
	if (kot(parent->_data) > kot(data))
	{
		parent->_left = cur;
	}
	else
	{
		parent->_right = cur;
	}
	cur->_col = Red;
	while (parent && parent->_col == Red)
	{
		Node* grandfather = parent->_parent;
		if (grandfather->_left == parent)
		{
			Node* uncle = grandfather->_right;
			if (uncle && uncle->_col == Red)
			{
				uncle->_col = parent->_col = Black;
				grandfather->_col = Red;
				cur = grandfather;
				parent = cur->_parent;
			}
			else
			{
				if (parent->_left == cur)
				{
					RotateR(grandfather);
					parent->_col = Black;
					grandfather->_col = Red;
				}
				else
				{
					RotateL(parent);
					RotateR(grandfather);
					cur->_col = Black;
					grandfather->_col = Red;
				}
				break;
			}
		}
		else
		{
			Node* uncle = grandfather->_left;
			if (uncle && uncle->_col == Red)
			{
				uncle->_col = parent->_col = Black;
				grandfather->_col = Red;
				cur = grandfather;
				parent = cur->_parent;
			}
			else
			{
				if (parent->_right == cur)
				{
					parent->_col = Black;
					grandfather->_col = Red;
				}
				else
				{
					RotateR(parent);
					RotateL(grandfather);
					grandfather->_col = Red;
					cur->_col = Black;
				}
				break;
			}
		}
	}
	_root->_col = Black;
	return { Iterator(newnode,_root),true };
}

再对myset和mymap进行改造：

//myset
pair<iterator,bool> insert(const K& key)
{
	return _t.Insert(key);
}

如果对于mymap则不仅需要改造insert函数，还需要完成operator[]的实现这个时候我们需要返回值的类型是V&，我们需要接收一下insert的返回值，如：pair<iterator,bool> ret=_t.Insert({key,V()});我们这样写的目的是mymap对RBTree的模板参数T实例化为pair<const K,V>了，所以需要构造一个pair对象进行传入，然后我们需要返回这个返回值的iterator里的值，因为iterator实际上存储的还是一个pair对象，所以要返回的是值，为second，所以写成了如下奇怪的形式：

ret.first->second;

再解释一遍是Insert返回的是插入的值的迭代器作为键，是否插入成功的结果作为值，我们想得到的是键，所以用对象.first访问到，而iterator本质上是存储了一个键值对的，而访问只能通过迭代器->second或者->first进行，（也可以*(对象).first和*(对象).second进行），但是为了方便理解，这里就用->形式了。

总之我们用operator[]的结果就是为了得到键对应的值，而我们调用Insert的目的是避免重复插入并且返回最终该值对应的迭代器，而该迭代器是存储了一个键值对的，我们要得到传入的键所对应的值，所以要这样写，所以在mymap中：

//mymap
pair<iterator,bool> insert(const pair<K,V>& kv)
{
	return _t.Insert(kv);
}
V& operator[](const K& key)
{
	pair<iterator, bool> ret = _t.Insert({ key,V() });//调用V对应的类型的构造函数初始化该键对应的值
	return ret.first->second;
}

11.代码汇总

在map和set中重要的函数已经实现了，像什么:

剩余的函数感兴趣的可以自行实现一下，掌握到这个地步已经可以了。

以下是三个文件的代码：

//myset.h
#include"RBTree.h"
template<class K>
class myset
{
	struct SetKeyOfT
	{
		const K& operator()(const K& key)
		{
			return key;
		}
	};
public:
	//typedef typename RBTree<K, K, SetKeyOfT>::Iterator iterator;
	//using iterator = typename RBTree<K, K, SetKeyOfT>::Iterator;
	//下面两种随意选
	//typedef typename RBTree<K,const K, SetKeyOfT>::Iterator iterator;
	using iterator = typename RBTree<K, const K, SetKeyOfT>::Iterator;
	//下面两种随意选：
	//typedef typename RBTree<K, K, SetKeyOfT>::ConstIterator const_iterator;
	//using const_iterator = typename RBTree<K, K, SetKeyOfT>::ConstIterator;
	//下面两种随意选
	//typedef typename RBTree<K,const K, SetKeyOfT>::ConstIterator const_iterator;
	using const_iterator = typename RBTree<K,const K, SetKeyOfT>::ConstIterator;
	pair<iterator,bool> insert(const K& key)
	{
		return _t.Insert(key);
	}
	iterator begin()
	{
		return _t.Begin();
	}
	iterator end()
	{
		return _t.End();
	}
	const_iterator begin() const
	{
		return _t.Begin();
	}
	const_iterator end() const
	{
		return _t.End();
	}
private:
	//RBTree<K, K, SetKeyOfT> _t;
	RBTree<K, const K, SetKeyOfT> _t;
};
//mymap.h
#include"RBTree.h"
template<class K,class V>
class mymap
{
	struct MapKeyOfT
	{
		const K& operator()(const pair<K, V>& kv)
		{
			return kv.first;
		}
	};
public:
	//typedef typename RBTree<K, pair<K, V>, MapKeyOfT>::Iterator iterator;
	//using iterator = typename RBTree<K, pair<K, V>, MapKeyOfT>::Iterator;
	//下面两种随便选一种
	//typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::Iterator iterator;
	using iterator = typename RBTree<K, pair<const K, V>, MapKeyOfT>::Iterator;
	//下面两种随便选一种
	//typedef typename RBTree<K, pair<K, V>, MapKeyOfT>::ConstIterator const_iterator;
	//using const_iterator = typename RBTree<K, pair<K, V>, MapKeyOfT>::ConstIterator;
	//下面两种随便选一种
	//typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::ConstIterator const_iterator;
	using const_iterator = typename RBTree<K, pair<const K, V>, MapKeyOfT>::ConstIterator;
	pair<iterator,bool> insert(const pair<K,V>& kv)
	{
		return _t.Insert(kv);
	}
	V& operator[](const K& key)
	{
		pair<iterator, bool> ret = _t.Insert({ key,V() });//调用V对应的类型的构造函数初始化该键对应的值
		return ret.first->second;
	}
	iterator begin()
	{
		return _t.Begin();
	}
	iterator end()
	{
		return _t.End();
	}
	const_iterator begin() const
	{
		return _t.Begin();
	}
	const_iterator end() const
	{
		return _t.End();
	}
private:
	//RBTree<K, pair<K, V>, MapKeyOfT> _t;
	RBTree<K, pair<const K, V>, MapKeyOfT> _t;
};
//RBTree.h
#define _CRT_SECURE_NO_WARNINGS 1
#include <assert.h>
#include<vector>
#include<iostream>
using namespace std;
enum Color
{
	Red,
	Black
};
template<class T>
struct RBTreeNode
{
	T _data;//存放数据，可以传递T为pair类型
	RBTreeNode<T>* _parent;
	RBTreeNode<T>* _left;
	RBTreeNode<T>* _right;
	Color _col;
	RBTreeNode(const T& data)
		:_data(data)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
	{
	}
};
template<class T,class Ref,class Ptr>
struct _TreeIterator
{
	typedef RBTreeNode<T> Node;
	typedef _TreeIterator<T, Ref, Ptr> Self;//Ref:引用，Ptr:指针
	Node* _node;
	Node* _root;
	_TreeIterator(Node* node,Node* root)
		:_node(node)
		,_root(root)
	{ }
	Ref operator*()
	{
		return _node->_data;
	}
	Ptr operator->()
	{
		return &_node->_data;
	}
	bool operator!=(const Self& s)
	{
		return _node != s._node;
	}
	bool operator==(const Self& s)
	{
		return _node == s._node;
	}
	//后置++
	Self operator++(int)
	{
		Self tmp = *this;  // 保存当前状态
		++(*this);         // 调用前置++实现
		return tmp;        // 返回旧值
	}
	//后置--
	Self operator--(int)
	{
		Self tmp = *this;  // 保存当前状态
		--(*this);         // 调用前置--实现
		return tmp;        // 返回旧值
	}
	//前置++
	Self& operator++()
	{
		//中序遍历，这个时候就需要访问右孩子
		if (_node->_right)
		{
			//找右子树的最左结点
			_node = _node->_right;
			while (_node->_left)
			{
				_node = _node->_left;
			}
		}
		else
		{
			//右子树为空
			//对应15结点或者50结点
			Node* cur = _node;
			Node* parent = cur->_parent;
			//当parent不为空，且cur为parent的右孩子是继续往上
			//因为这代表该子树已经遍历完了
			while (parent && cur == parent->_right)
			{
				cur = parent;
				parent = cur->_parent;
			}
			//要么cur是parent的左孩子，这个时候就可以直接用_node=parent
			//这两种情况都可以这样写
			_node = parent;
		}
		return *this;
	}
	//前置--
	Self& operator--()
	{
		if (_node == nullptr) // end()
		{
			// --end()，特殊处理，⾛到中序最后⼀个结点，整棵树的最右结点
			Node* rightMost = _root;
			while (rightMost && rightMost->_right)
			{
				rightMost = rightMost->_right;
			}
			_node = rightMost;
		}
		else if (_node->_left)
		{
			//代表该子树还没遍历完
			//找左子树的最右结点
			_node = _node->_left;
			while (_node->_right)
			{
				_node = _node->_right;
			}
		}
		else
		{
			//该子树被遍历完
			//向上查找，直到查找到根或者该孩子为父亲的右孩子
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && cur == parent->_left)
			{
				cur = parent;
				parent = cur->_parent;
			}
			_node = parent;
		}
		return *this;
	}
};
template<class K,class T,class KeyOfT>
class RBTree
{
public:
	typedef RBTreeNode<T> Node;
	typedef _TreeIterator<T, T&, T*> Iterator;
	typedef _TreeIterator<T, const T&, const T*> ConstIterator;
	void RotateR(Node* parent)
	{
		assert(parent != nullptr);
		Node* subL = parent->_left;
		assert(subL != nullptr);
		Node* subLR = subL->_right;
		parent->_left = subLR;
		subL->_right = parent;
		if (subLR)
		{
			subLR->_parent = parent;
		}
		Node* parentParent = parent->_parent;
		parent->_parent = subL;
		if (parent == _root)
		{
			subL->_parent = nullptr;
			_root = subL;
		}
		else
		{
			if (parentParent->_left == parent)
			{
				parentParent->_left = subL;
			}
			else
			{
				parentParent->_right = subL;
			}
			subL->_parent = parentParent;
		}
	}
	void RotateL(Node* parent)
	{
		assert(parent != nullptr);
		Node* subR = parent->_right;
		assert(subR != nullptr);
		Node* subRL = subR->_left;
		parent->_right = subRL;
		if (subRL)
		{
			subRL->_parent = parent;
		}
		subR->_left = parent;
		Node* parentParent = parent->_parent;
		parent->_parent = subR;
		if (parent == _root)
		{
			subR->_parent = nullptr;
			_root = subR;
		}
		else
		{
			if (parentParent->_left == parent)
			{
				parentParent->_left = subR;
			}
			else
			{
				parentParent->_right = subR;
			}
			subR->_parent = parentParent;
		}
	}
	pair<Iterator,bool> Insert(const T& data)
	{
		if (_root == nullptr)
		{
			_root = new Node(data);
			_root->_col = Black;
			return { Iterator(_root,_root),true };//隐式类型转换
		}
		KeyOfT kot;
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			if (kot(cur->_data) > kot(data))
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (kot(cur->_data) < kot(data))
		    {
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return { Iterator(cur,_root),true };
			}
		}
		cur = new Node(data);
		Node* newnode = cur;
		cur->_parent = parent;
		if (kot(parent->_data) > kot(data))
		{
			parent->_left = cur;
		}
		else
		{
			parent->_right = cur;
		}
		cur->_col = Red;
		while (parent && parent->_col == Red)
		{
			Node* grandfather = parent->_parent;
			if (grandfather->_left == parent)
			{
				Node* uncle = grandfather->_right;
				if (uncle && uncle->_col == Red)
				{
					uncle->_col = parent->_col = Black;
					grandfather->_col = Red;
					cur = grandfather;
					parent = cur->_parent;
				}
				else
				{
					if (parent->_left == cur)
					{
						RotateR(grandfather);
						parent->_col = Black;
						grandfather->_col = Red;
					}
					else
					{
						RotateL(parent);
						RotateR(grandfather);
						cur->_col = Black;
						grandfather->_col = Red;
					}
					break;
				}
			}
			else
			{
				Node* uncle = grandfather->_left;
				if (uncle && uncle->_col == Red)
				{
					uncle->_col = parent->_col = Black;
					grandfather->_col = Red;
					cur = grandfather;
					parent = cur->_parent;
				}
				else
				{
					if (parent->_right == cur)
					{
						parent->_col = Black;
						grandfather->_col = Red;
					}
					else
					{
						RotateR(parent);
						RotateL(grandfather);
						grandfather->_col = Red;
						cur->_col = Black;
					}
					break;
				}
			}
		}
		_root->_col = Black;
		return { Iterator(newnode,_root),true };
	}
	Iterator Begin()
	{
		Node* minleft = _root;
		while (minleft && minleft->_left)
		{
			minleft = minleft->_left;
		}
		//调用_TreeIterator
		//相当于_TreeIterator(minleft)
		return Iterator(minleft, _root);
	}
	Iterator End()
	{
		return Iterator(nullptr, _root);
	}
	ConstIterator Begin() const
	{
		Node* minleft = _root;
		while (minleft && minleft->_left)
		{
			minleft = minleft->_left;
		}
		return ConstIterator(minleft, _root);
	}
	ConstIterator End() const
	{
		return ConstIterator(nullptr, _root);
	}
	bool Find(const K& key)
	{
		KeyOfT kot;
		Node* cur = _root;
		while (cur)
		{
			if (kot(cur->_data) < key)
			{
				cur = cur->_right;
			}
			else if (kot(cur->_data) > key)
			{
				cur = cur->_left;
			}
			else
			{
				return true;
			}
		}
		return false;
	}
	bool Check(Node* root, int blackNum, const int refNum)
	{
		if (root == nullptr)
		{
			if (refNum != blackNum)
			{
				cout << "存在⿊⾊结点的数量不相等的路径" << endl;
				return false;
			}
			return true;
		}
		if (root->_col == Red && root->_parent->_col == Red)
		{
			cout << root->_kv.first << "存在连续的红⾊结点" << endl;
			return false;
		}
		if (root->_col == Black)
		{
			blackNum++;
		}
		return Check(root->_left, blackNum, refNum)
			&& Check(root->_right, blackNum, refNum);
	}
	bool IsBalance()
	{
		if (_root == nullptr)
			return true;
		if (_root->_col == Red)
			return false;
		int refNum = 0;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_col == Black)
			{
				++refNum;
			}
			cur = cur->_left;
		}
		return Check(_root, 0, refNum);
	}
	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}
	void _InOrder(Node* root)
	{
		if (root == nullptr)
		{
			return;
		}
		_InOrder(root->_left);
		cout << root->_kv.first << " ";
		_InOrder(root->_right);
	}
private:
	Node* _root = nullptr;
};

12.总结

map和set和红黑树在C++进阶中都算比较重要的知识，如果能学会这些就比较厉害了，封装红黑树实现map和set的逻辑性比较强，建议各位加以理解。

好了，该讲内容就到这里，下讲将讲解C++进阶-哈希（非常重要），哈希理解起来不是很难，但是实现的时候可能难度比较高，所以各位做好心理准备哦。

喜欢的可以一键三连哦，下讲再见！

C++STL详解(九)--使用红黑树封装实现set和map
清欢Allen的技术博客
04-19 802
如果我们用一棵KV模型的红黑树同时实现map和set,我们就需要控制map和set中的所传入红黑树中的模板参数,其中,封装过程中,为了与红黑树的模板参数区分,我们将红黑树中模板参数由V改成T.在插入中,结点中存储的类型T可能为Set容器中的key,也有可能是Map中的pair键值对,底层红黑树如何针对不同类型的容器进行比较呢?所以,当容器为set时,红黑树中的仿函数就实例化为set容器中的仿函数,当容器为map时,红黑树中的仿函数就实例化为map中的仿函数.正向迭代器还包括了==,!
【C++】用红黑树封装set和map
春风不语。
11-13 1103
本篇内容到这里就结束啦，主要讲了如何用红黑树来封装set和map容器，希望对大家有帮助，祝生活愉快！
C++进阶--红黑树模拟实现STL中的map和set
sushang的博客
01-15 1369
因此，上层容器map需要向底层红黑树提供一个仿函数，用于获取T当中的键值Key，这样一来，当底层红黑树当中需要比较两个结点的键值时，就可以通过这个仿函数来获取T当中的键值了。但是对于底层红黑树来说，它并不知道上层容器是map还是set，因此需要进行两个结点键值的比较时，底层红黑树都会通过传入的仿函数来获取键值Key，进而进行两个结点键值的比较。这样一来，当底层红黑树需要进行两个结点之间的键值的比较时，都会通过传入的仿函数来获取相应结点的键值，然后再进行比较。
C++进阶——封装红黑树实现map和set
博客 | 复习知识点 + 练习 + 最终的领悟 | 全力以赴
03-22 1126
(整个子树已经访问完了，如果这个子树是外面的右子树，那么外面一层的子树也访问完了，直到子树是外面子树的左子树，左子树访问完了，访问中)，就访问，2. 源码中的pair的<比较，比较了key和value，但是。MySet是为了兼容MyMap，所以也要实现。)，相当于外层左边的子树访问完了，然后访问中。然后更新迭代器中的节点指针，返回*this。修改RBtree中的insert返回值为。，在右子树中进行，左中右，访问。1. 这里相比源码调整一下，当左为空，表示左访问完了，就是走右中左，基本相同。
C++ -- 红黑树模拟实现map和set
m0_73573757的博客
03-23 869
根据现有了解，我们知道set中存储的应当只有key，而map中存储的应该是<key, value>的键值对，但实际是这样吗？我们去库中(stl_set.h)查看相关定义(此处省略了部分代码，不影响理解)：上图分别是库中关于set、map和红黑树的相关定义。并不像我们想的那样,set中也有key_type和value_type，但实际上两者的类型都是Key；
C++进阶--使用红黑树封装map和set
2402_87779153的博客
05-11 939
红黑树封装mymap，myset，红黑树中迭代器的接口实现，实现的步骤
C++进阶：封装红黑树实现map和set
2301_81699364的博客
11-02 986
RBTree实现了泛型不知道T参数导致是K，还是pair，那么insert内部进行插入逻辑比较时，就没办法进行比较，因为pair的默认支持的是key和value一起参与比较，我们需要时的任何时候只比较key，所以我们在map和set层分别实现一个MapKeyOfT和SetKeyOfT的仿函数传给 RBTree的KeyOfT，然后RBTree中通过KeyOfT仿函数取出T类型对象中的key，再进行比较，具体细节参考如下代码实现。如果右子树为空，就需要往上找了，找的是孩子是父亲左的那个祖先。
C++----红黑树&&map和set的封装
2403_82706967的博客
03-08 1166
/ map侧迭代器定义// set侧迭代器定义关键差异容器迭代器类型可修改性map普通迭代器可修改value，不可修改keysetconst迭代器完全不可修改元素。
C++进阶--哈希表模拟实现unordered_set和unordered_map
sushang的博客
01-21 1324
哈希表里面具体存的是什么类型的元素，是由模板参数T来决定如果是unordered_set，传给T就是Key如果是unordered_map，传给T的就是pair哈希表结点结构T _data;{}迭代器的结构：注意：哈希表迭代器封装的是结点指针和哈希表指针，因为要在哈希表中找下一个桶，所以要用到哈希表指针在构造正向迭代器时，我们不仅需要对应哈希结点的指针，还需要该哈希结点所在哈希表的地址。
STL详解 - 红黑树模拟实现map与set
天行健、君子以自强不息
05-12 817
用红黑树封装map和set
C++--红黑树封装实现set和map
Tanecious的博客
07-13 745
为了让 end() 能够指向最右节点的下一个节点， stl 源码中增加了一个哨兵位的头结点，该节点的 left 指向这棵树的最左节点，也就是 begin()，right 指向这棵树的最右节点，parent 指向 nullptr，然后让根的父节点指向它，最右节点的 right 也指向它，所以在 stl 源码的实现中这个哨兵位头结点就是 end()。如图：it指向11，11右为空，11是8的右，11所在子树访问完了，8所在子树也访问完了，继续往上找，8是13的左，那么下一个访问的结点就是13。
【C++进阶】 用红黑树封装map和set
Weraphael的博客
01-20 1142
模拟实现map和set
C++红黑树封装实现map和set模拟
本资源将通过封装红黑树来模拟实现map和set。红黑树是一种自平衡的二叉搜索树，通过对插入和删除操作的特定处理，它可以保证最坏情况下的时间复杂度为O(log n)，这对于需要高效搜索和插入操作的场景非常有用。 在...
【C++】红黑树详解并封装实现map和set
love_guanghui的博客
03-18 3400
红黑树详解
C++ 中 initializer_list&& 类型推导
2510_91653061的博客
08-04 290
右值引用可以绑定到将要销毁的临时对象，从而实现资源的转移，而不是复制。本身是一个轻量级的对象，通常包含对数据的引用和大小的信息，因此没有必要通过右值引用来转移它的所有权。是一种用于表示列表初始化的标准库模板类，提供了一种方便的方式来初始化容器或者进行函数调用时传递一组参数。类型推导涉及到右值引用和移动语义，这在现代 C++ 中变得越来越重要。上没有特别的性能优势，但它可以用于理解右值引用和类型推导的概念。与右值引用结合使用时，涉及到类型推导和资源管理的问题。类型的参数，并打印出列表中的所有元素。
C++ vector模拟实现
chj_1206的博客
08-01 674
为了更好的去了解vector底层，便于我们模拟实现，我们寻找适合自己的头文件源代码去阅读。我们能够发现vector的成员变量，然后我们大胆进行初步的猜测。当然不能仅仅通过猜测就能去确定，所以我们继续去研究核心接口大概怎么实现。这就是vector的构造函数我们找到push_back能够发现跟我们所想的差不多，end_of_storage是空间结束位置，finsh是数据结束位置，start就应该是开始位置了。再通过下面代码，我们就能够确定我们之前的猜测是没有问题的了。一、成员变量。
《C++》stack容器详解
Maysheeo的博客
08-03 840
C++中的stack详解
C++：STL中的栈和队列的适配器deque
lrhhappy的博客
08-03 946
本文主要探讨了C++中容器适配器stack和queue的底层实现原理及其优势。通过分析deque（双端队列）的特性，解释了其作为stack和queue默认底层容器的原因：deque在头部和尾部操作效率高（O(1)），且空间利用率优于list，同时避免了vector扩容时的数据迁移问题。文章详细比较了不同容器的优缺点，指出deque虽不适合遍历，但完美适配stack和queue只需单端操作的需求。此外，还介绍了优先级队列的模拟实现，重点阐述了堆结构如何通过向上/向下调整算法维护特性，确保O(logn)时间复杂
【C++】石头剪刀布游戏
最新发布
C语言实战大全
08-04 977
课程设计实现，包含面向对象设计、随机数生成、胜负判定等功能，适合课程设计或编程练习~
评论 3
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

刚入门的大一新生

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值