算法入门之并查集

并查集

学习

并查集有两种实现方法：

实现方法一

通过所在集合最小的元素作为该集合的标记。这种方法的查找元素属于某个集合很快，但是合并很慢。举例如下：

/*
 *假设这里有1~8这几个数字，分别属于几个集合
 *      数组：1 2 1 4 1 2 4 1
 *分别对应i = 1 2 3 4 5 6 7 8 (i = 0忽略不看)
 *存储数字为集合中最小的那个数字
 *也就是说1、3、5、8属于一个集合
 * 以此类推
 */
#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
#define int long long

using namespace std;

vector<int> arr(9);

int find(int x) {
	return arr[x];
}

void merge(int a, int b) {
	int minn = min(a, b);
	int  maxx = max(a, b);
	for (auto it = arr.begin() + 1; it != arr.end(); ++it) {
		if (*it == maxx) *it = minn;
	}
}

signed main(void)
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);

	arr = {0, 1, 2, 1, 4, 1, 2, 4, 1 };
	cout << "元素1属于集合" << find(1) << endl;
	cout << "元素2属于集合" << find(2) << endl;
	//对元素1和2所在集合合并
	merge(1, 2);
	cout << "元素2属于集合" << find(2) << endl;

	return 0;
}

不难看出，这种方法的查找效率是O(1)，合并效率是O(n)。显然合并时的效率不够高，需要遍历一遍数组。

实现方法二

每个集合通过一个有根树表示。也就是说，如果几个元素在同一个集合内，除了根节点保存自己以外，其他节点均保存父节点。举例如下:

/*
* 假设还是1~8个数字，分别属于几个集合
* 数组：  1 2 3 4 3 4 3 1
* 对应i = 1 2 3 4 5 6 7 8 (同样不把i=0算进去)
* 可以得到{1，8}
*        {2}
*        {3，5，7}
*        {4，6}
 */
#include <iostream>
#include <vector>
#include <algorithm>
#define int long long

using namespace std;

vector<int> arr(9);

int find(int x) {
	while (arr[x] != x) {
		x = arr[x];
	}
	return x;
}

void merge(int a, int b) {
	arr[b] = a;
}

signed main(void)
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);

	arr = { 0, 1, 2, 3, 4, 3, 4, 3, 1 };
	cout << "元素8的集合是" << find(8) << endl;
	cout << "元素7的集合是" << find(7) << endl;
	merge(1, 3);
	cout << "元素7的集合是" << find(7) << endl;

	return 0;
}

但是，我们发现，虽然合并的效率提高了，但是查找的效率变慢了。不难看出，查找最坏的情况是链状树，也就是最坏复杂度为O(n)；而合并的复杂度变成了O(1)。

实现方法二的优化

看到这里，我知道你想说，两种实现方法各有优劣，都不能很好的实现并查集的功能。但是，你先别急，让我先急。第二种方法其实是可以通过路径压缩将O(n)的复杂度在每次查询的过程中优化。实际上，基本思路就是让其在查询的过程中，让所经过的节点都指向根节点。

//此时重新写一下查找代码，其他部分一样
//这是一个递归写法，看不懂的可以画个图理解理解
int find(int x) {
    if(arr[x] != x) {
        arr[x] = find(arr[x]);
    }
    return arr[x];
}

好了，到此并查集的学习就结束了。下面就是刷题环节。

训练

题目是按照由易到难的顺序排序的。

P3367 【模板】并查集

题目背景

本题数据范围已经更新到 $1\le N\le 2\times 10^5$，$1\le M\le 10^6$。

题目描述

如题，现在有一个并查集，你需要完成合并和查询操作。

输入格式

第一行包含两个整数 $N,M$ ,表示共有 $N$ 个元素和 $M$ 个操作。

接下来 $M$ 行，每行包含三个整数 $Z_i,X_i,Y_i$ 。

当 $Z_i=1$ 时，将 $X_i$ 与 $Y_i$ 所在的集合合并。

当 $Z_i=2$ 时，输出 $X_i$ 与 $Y_i$ 是否在同一集合内，是的输出
Y ；否则输出 N 。

输出格式

对于每一个 $Z_i=2$ 的操作，都有一行输出，每行包含一个大写字母，为 Y 或者 N 。

输入输出样例 #1

输入 #1

4 7
2 1 2
1 1 2
2 1 2
1 3 4
2 1 4
1 2 3
2 1 4

输出 #1

N
Y
N
Y

说明/提示

对于 $15\%$ 的数据，$N\le 10$，$M\le 20$。

对于 $35\%$ 的数据，$N\le 100$，$M\le 10^3$。

对于 $50\%$ 的数据，$1\le N\le 10^4$，$1\le M\le 2\times 10^5$。

对于 $100\%$ 的数据，$1\le N\le 2\times 10^5$，$1\le M\le 10^6$，$1\le X_i,Y_i\le N$， Z i ∈ { 1 , 2 } Z_i \in \{ 1, 2 \} Zi​∈{1,2}。

题解

对于刚刚学完并查集，并且看过代码的这么聪明的你来说，这个应该挺简单的。直接给ac代码了，如下：

#include <bits/stdc++.h>
#define int long long

using namespace std;

vector<int> arr(200001, 0);
int n, m;

int find(int x) {
    if(arr[x] != x) {
        arr[x] = find(arr[x]);
    }
    return arr[x];
}

void merge(int a, int b) {
    arr[a] = b;
}

signed main(void) 
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    cin >> n >> m;
    iota(arr.begin(), arr.begin() + n + 1, 0);
    while(m--) {
        int z, x, y;
        cin >> z >> x >> y;
        if(z == 1) {
            merge(find(x),find(y));
        } 
        else {
            if(find(x) == find(y)) 
                cout << "Y" << endl;
            else 
                cout << "N" << endl;
        }
    }

    return 0;
}

[NOIP2010]关押罪犯

S 城现有两座监狱，一共关押着N 名罪犯，编号分别为1~N。他们之间的关系自然也极不和谐。很多罪犯之间甚至积怨已久，如果客观条件具备则随时可能爆发冲突。我们用“怨气值”（一个正整数值）来表示某两名罪犯之间的仇恨程度，怨气值越大，则这两名罪犯之间的积怨越多。如果两名怨气值为c 的罪犯被关押在同一监狱，他们俩之间会发生摩擦，并造成影响力为c 的冲突事件。
每年年末，警察局会将本年内监狱中的所有冲突事件按影响力从大到小排成一个列表，然后上报到S 城Z 市长那里。公务繁忙的Z 市长只会去看列表中的第一个事件的影响力，如果影响很坏，他就会考虑撤换警察局长。
在详细考察了 N 名罪犯间的矛盾关系后，警察局长觉得压力巨大。他准备将罪犯们在两座监狱内重新分配，以求产生的冲突事件影响力都较小，从而保住自己的乌纱帽。假设只要处于同一监狱内的某两个罪犯间有仇恨，那么他们一定会在每年的某个时候发生摩擦。那么，应如何分配罪犯，才能使 Z 市长看到的那个冲突事件的影响力最小？这个最小值是多少？

#####输入描述:

第一行为两个正整数N和M，分别表示罪犯的数目以及存在仇恨的罪犯对数。 
接下来的M行每行为三个正整数aj，bj，cj，表示aj号和bj号罪犯之间存在仇恨，其怨气值为cj。
数据保证1≤aj＜bj≤N，0＜cj≤1,000,000,000，且每对罪犯组合只出现一次。

输出描述:

共1行，为Z市长看到的那个冲突事件的影响力。如果本年内监狱中未发生任何冲突事件，请输出0。                        

示例1

输入

4 6
1 4 2534
2 3 3512
1 2 28351
1 3 6618
2 4 1805
3 4 12884

输出

3512

说明

罪犯之间的怨气值如下面左图所示，右图所示为罪犯的分配方法，市长看到的冲突事件影响力是3512（由2号和3号罪犯引发）。其他任何分法都不会比这个分法更优。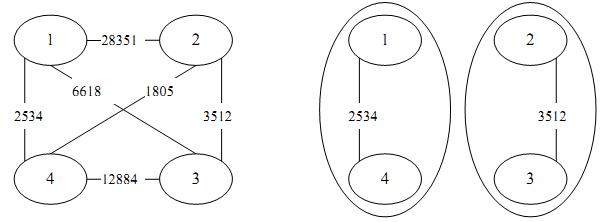

备注:

对于30%的数据有N≤15。
对于70%的数据有N≤2000，M≤50000。
对于100%的数据有N≤20000，M≤100000。

题解

这题有个血泪教训，vector的二维数组很吃空间，所以一直会内存超限，换成结构体的一维数组之后就好了。

#include <bits/stdc++.h>
using namespace std;

const int MAXN = 2e5 + 10;  

struct Edge {
    int u, v, w;
};

int n, m;
vector<int> arr(MAXN);
vector<int> enemy(MAXN, 0);
vector<Edge> num(MAXN);  

int find(int x) {
    return arr[x] == x ? x : arr[x] = find(arr[x]);
}

//这里的merge和之前的唯一区别就是查找根节点写在里外的区别
void merge(int a, int b) {
    int fa = find(a), fb = find(b);
    if (fa != fb) arr[fa] = fb;  
}

signed main() {
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);

    cin >> n >> m;
    if (n == 1) cout << 0 << endl;
    else {
        iota(arr.begin(), arr.begin() + n + 1, 0);
        for (int i = 1; i <= m; ++i) {
            cin >> num[i].u >> num[i].v >> num[i].w;
        }
        sort(num.begin() + 1, num.begin() + m + 1, [](const Edge& a, const Edge& b) {
            return a.w > b.w;
        });

        int cnt = 0;
        for (int i = 1; i <= m; ++i) {
            int u = num[i].u, v = num[i].v;
            if (find(u) == find(v)) {
                cout << num[i].w << endl;
                cnt++;
                break;
            }
            
            if (!enemy[u]) 
                enemy[u] = v;
            else 
                merge(v, enemy[u]);  
            
            if (!enemy[v]) 
                enemy[v] = u;
            else 
                merge(u, enemy[v]);
        }
        if (cnt == 0) cout << 0 << endl;
    }
    return 0;
}

这次并查集就先写到这吧，好像没找到什么适合并查集入门的题目。言止于此，若是有不当之处，欢迎指出。