拓扑排序，拓扑序列

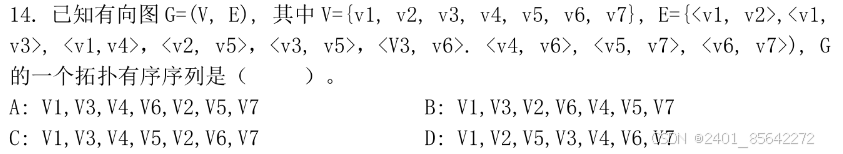
拓扑排序的概念

拓扑排序是一种针对有向无环图进行的排序方法。它将图中所有顶点排成一个线性序列，使得对于图中的每一条有向边(u, v)，顶点u在序列中都出现在顶点v之前。

对于一个有向无环图 G (V,E)来说，其拓扑排序是G中所有节点的一种线性次序，该次序满足如下条件：如果图G包含边(u,v)，则节点u在拓扑排序中处于节点v的前面。显然，如果图G包含环路，则不可能排出一个线性次序。

适用范围：

• 拓扑排序只适用于有向无环图。

结果非唯一：

• 对于同一个图，可能存在多个合法的拓扑排序序列。

不存在拓扑排序的情况：

• 如果图中含有环，则无法进行拓扑排序，因为环内的节点无法确定先后。

我们可以将图的拓扑排序看做是将图中的所有节点在同一水平线上排开，图的所有有向边都从左边指向右边，因此，图的拓扑排序与冒泡排序、堆排序等通常意义上的“排序”是不同的。

假定采用邻接表的方式存储图。拓扑排序的实现依赖于图的深度优先搜索DFS和广度优先搜索BFS算法。

 深度优先搜索实现拓扑排序

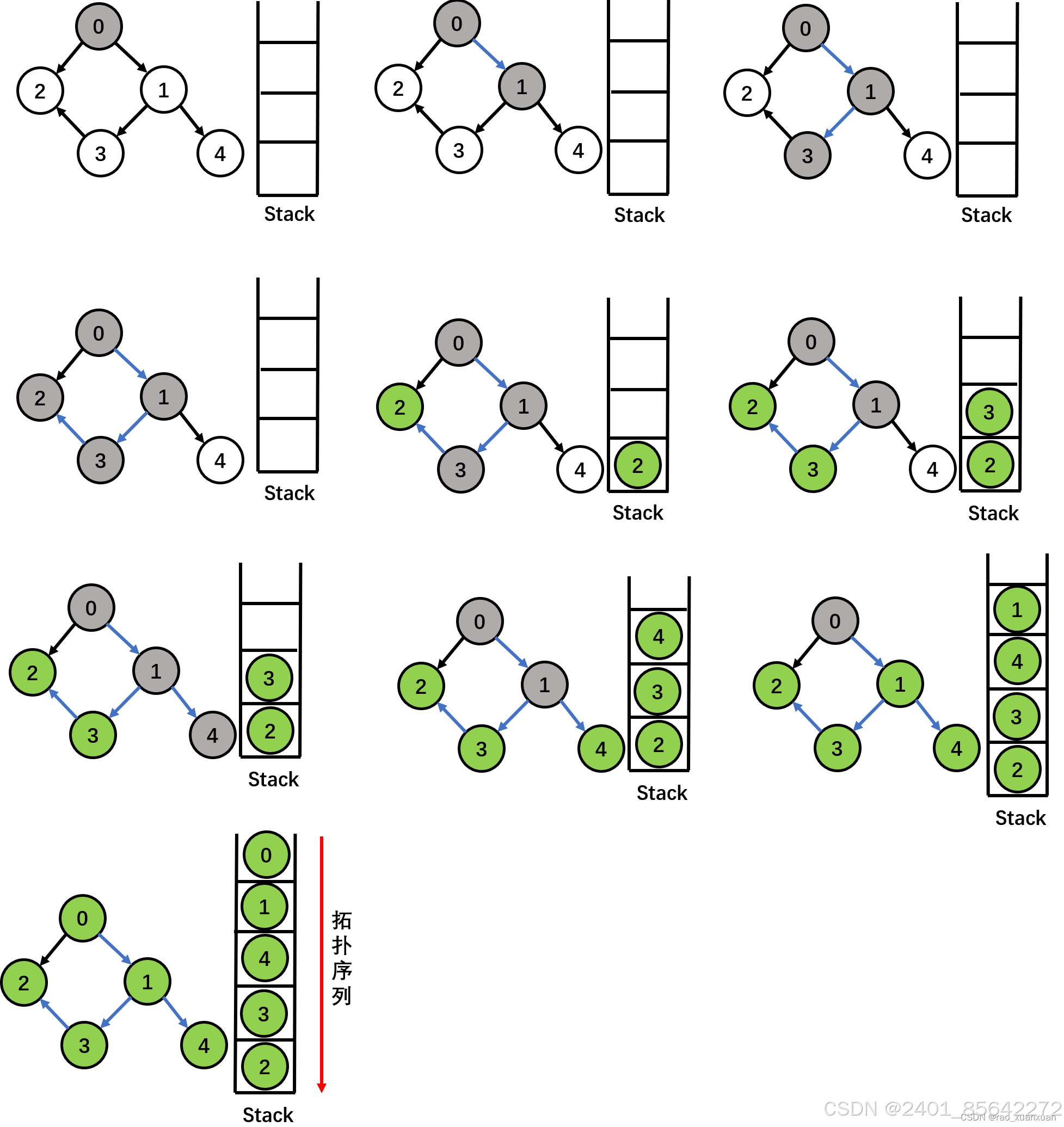
广度优先搜索实现拓扑排序

拓扑排序的方法

1、在有向图中选一个没有前驱的顶点且输出
2、从图中删除该顶点和所有以他为尾的弧
3、重复上述步骤，直到所有的顶点均已输出，或者当图中不存在无前驱的顶点为止

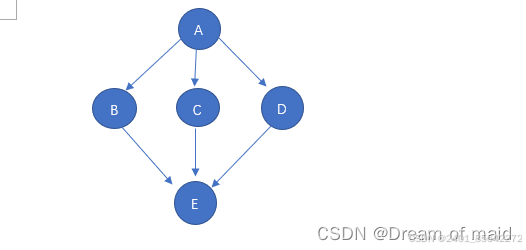
比如我们要对上述图进行拓扑排序 第一次寻找的是A这一个结点 因为A没有前驱 接下来就是删除A以及以A为弧尾的弧，此时就是如下图

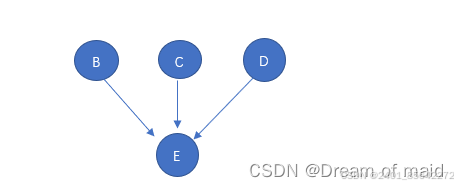
在从中选择一个没有前驱的结点，这里BCD 都可以，这里我们就选择B 同样的道理 删除B以及以B为弧尾的弧此时就是如下图

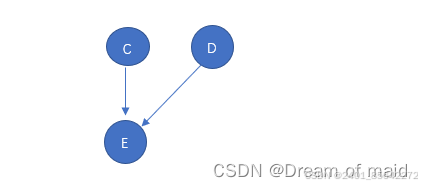
同样的道理 再选一个C删除以C为弧尾的弧

再删除 D

所有总的拓扑排序是 当然排序可能不止一种 因为可能不止一个结点在某一步骤中是无前驱的
ABCDE 有人可能会说了这个图太简单了，能不能难一点的图来拓扑
如下

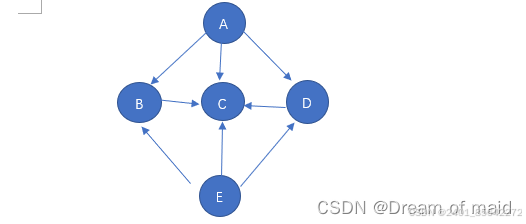
拓扑排序可以如下
AEBDC
EABDC
AEDBC
EADBC