排序方法--堆排序

对一组记录的关键码为(46，79，56，38，40，84)。如果采用堆排序方法，则建立的初始堆是（ ) 。
A: 79，46，56，38，40，84
B:84，56，79，40，46，38
D: 84，79，56，46，40，38
D:84，79，56，38，40，46

答案:D

 堆：是一种叫做完全二叉树的数据结构，分为大根堆，小分队。

堆排序：基于这种结构产生的一种程序算法。

堆的分类：

大根堆：每个结点的值都大于或者等于其左右孩子节点的值

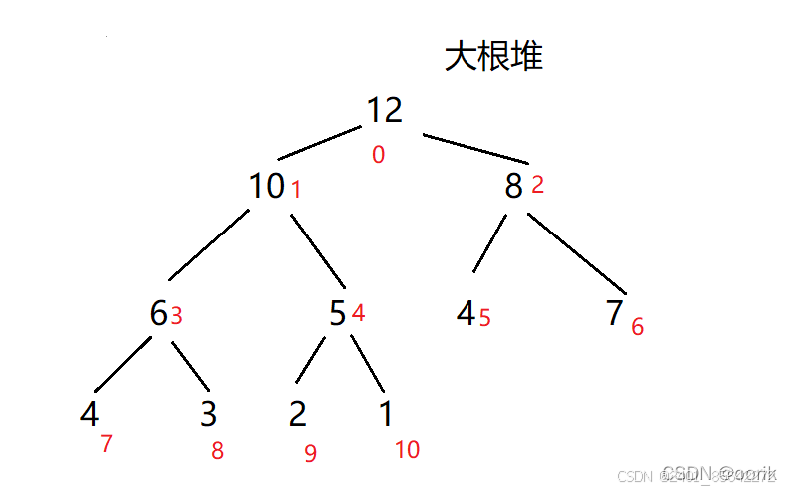
小根堆：每个节点的值都小于或者等于其左右孩子节点的值

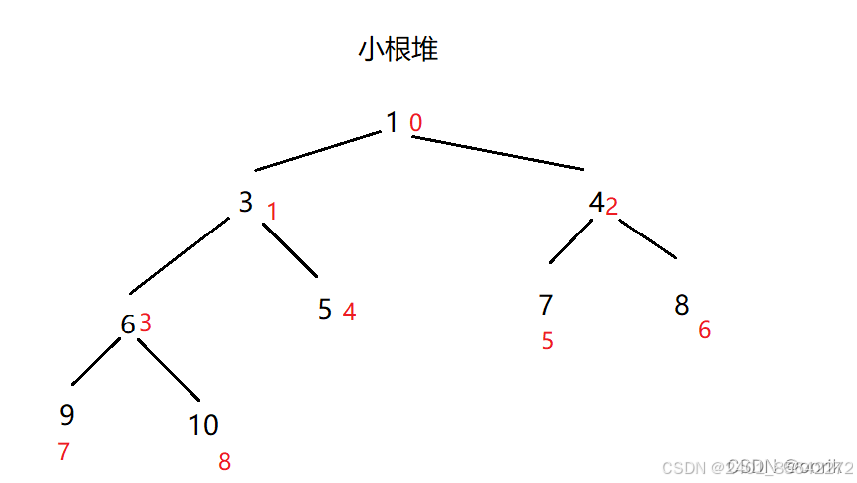
两种结构映射到数组：

大根堆

小根堆

 

下标

父-->子i-->左孩子2*i+1,右孩子2*i+2

子-->父i-->(i-1)/2

 排序思想

1.首先将待排序的数组构成一个大根堆，此时，整个数组的最大值就是堆结构的顶端

2.将顶端的数与末尾的数交换，此时，末尾的数为最大值，剩余待排序的数组个数为n-1

3.将剩余的n-1个数再构造成大根堆，再将顶端数与n-1位置的数交换，如此反复执行，便能得到有序数组

注意：升序用大根堆，降序用小根堆

构造堆

1.从最后一课子树开始，从后往前调整

2.每次调整，从上往下调整

3.调整为大根堆

首先给定一个无序的序列，将其看做一个堆结构，一个没有规则的二叉树，将序列里的值按照从上往下，从左到右依次填充到二叉树中。

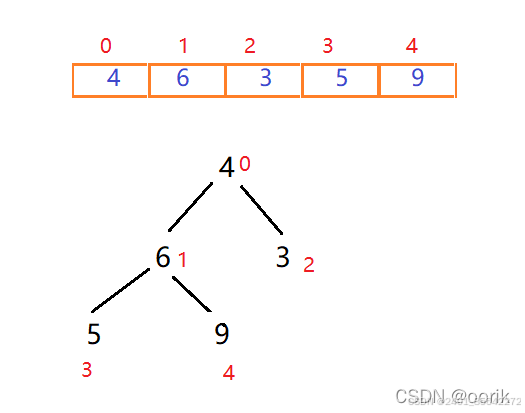
找到最后一个非叶子节点，即元素值为6的结点，比较它的左右节点中最大的一个值是否比它大，如果大就交换位置。

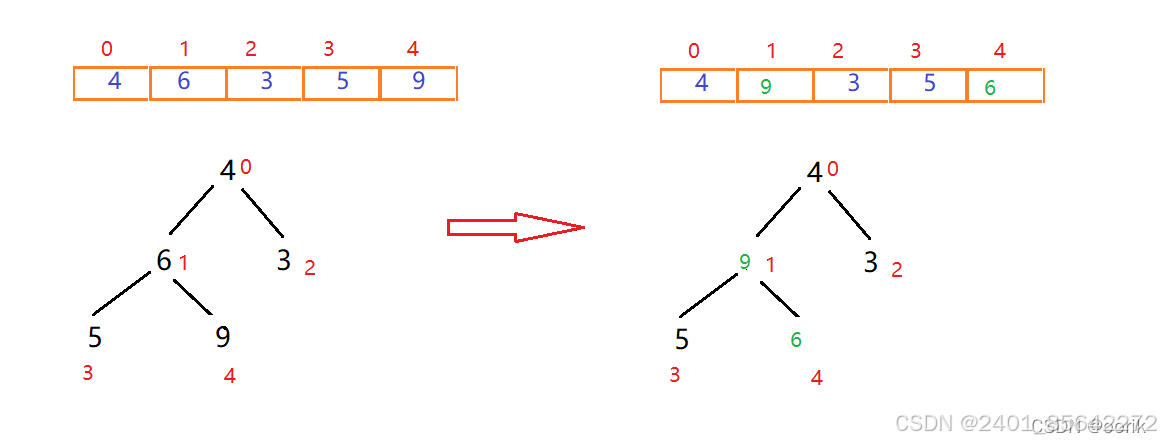
这里5小于6,9大于6，则交换9和6的位置

找到下一个非叶子节点4，用它和它的叶子结点进行比较，4大于3,4小于9，交换4和9的位置

 

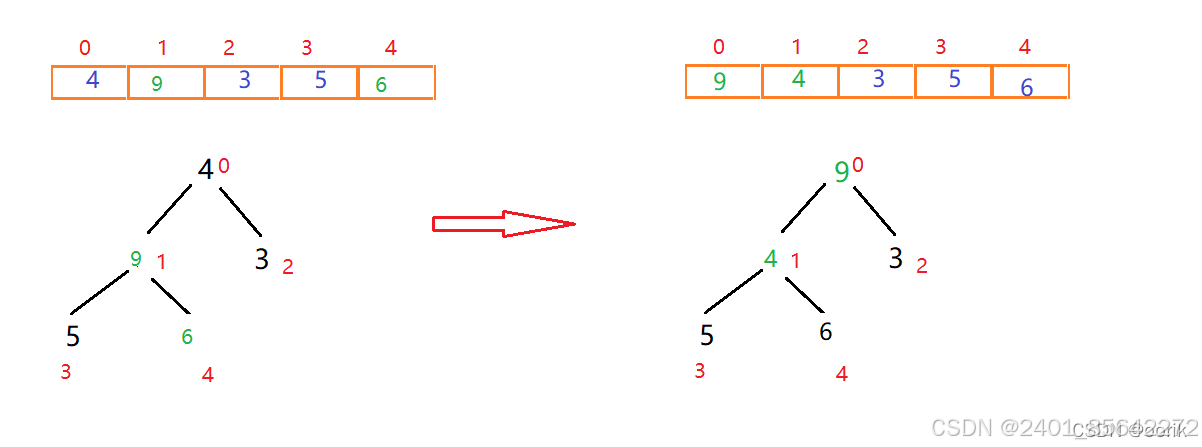
 此时发现4小于5和6这两个子节点，需进行调整，左右节点5和6中，6大于5且6大于父节点4，因此交换4和6的位置

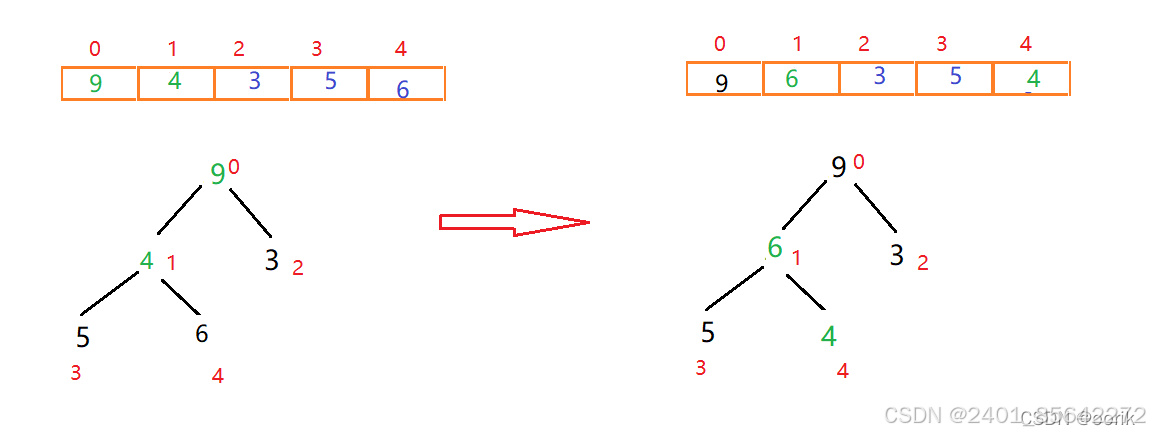
此时就构造出来一个大根堆，接下来进行排序

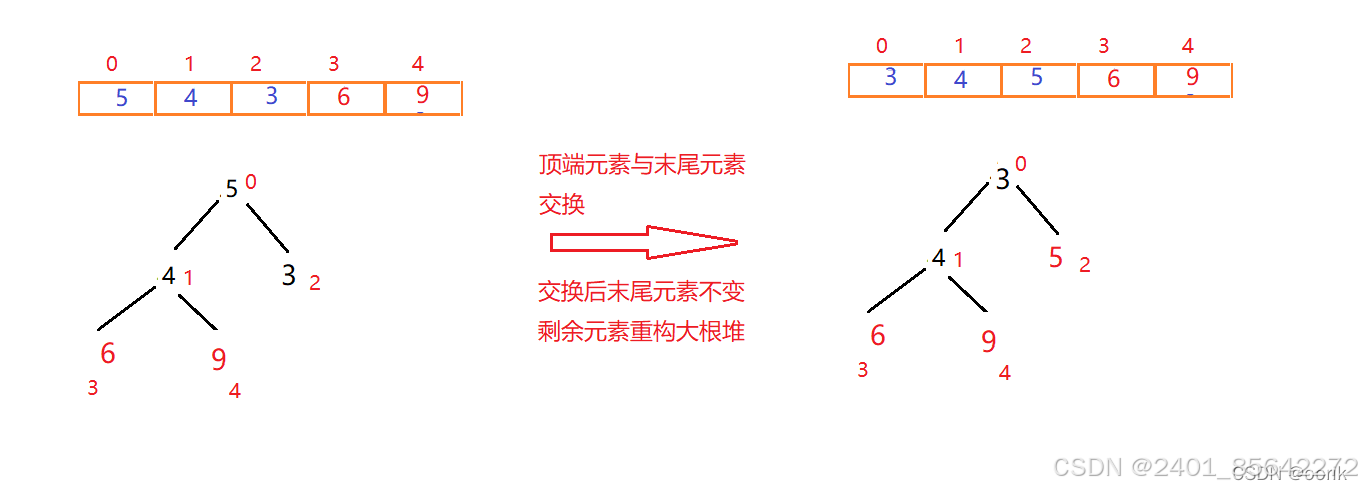
首先将顶点元素9与末尾元素4交换位置，此时末尾数字为最大值。排除已经确定的最大元素，将剩下元素重新构建大根堆

一次交换重构： 

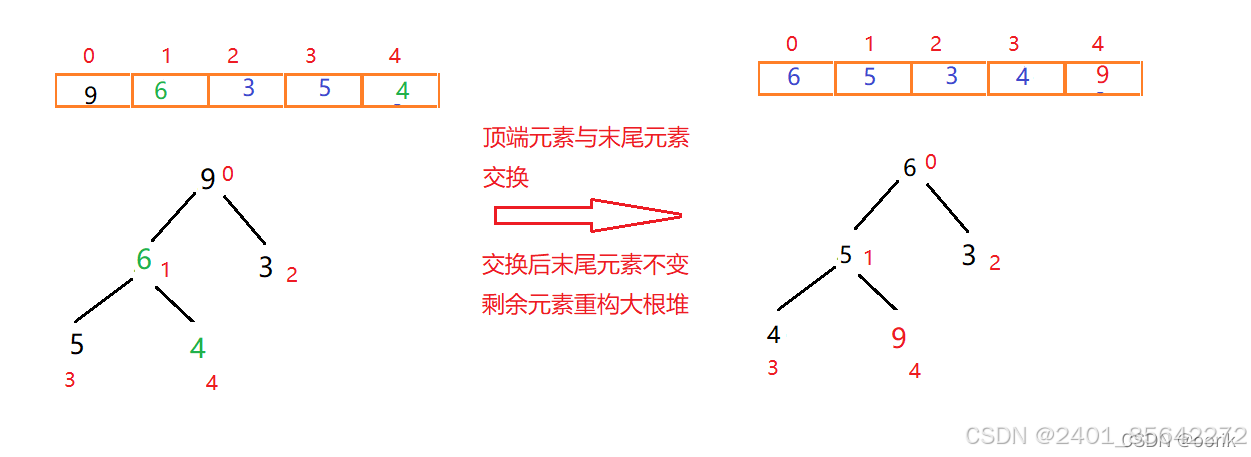
此时元素9已经有序，末尾元素则为4（每调整一次，调整后的尾部元素在下次调整重构时都不能动）

二次交换重构：

 

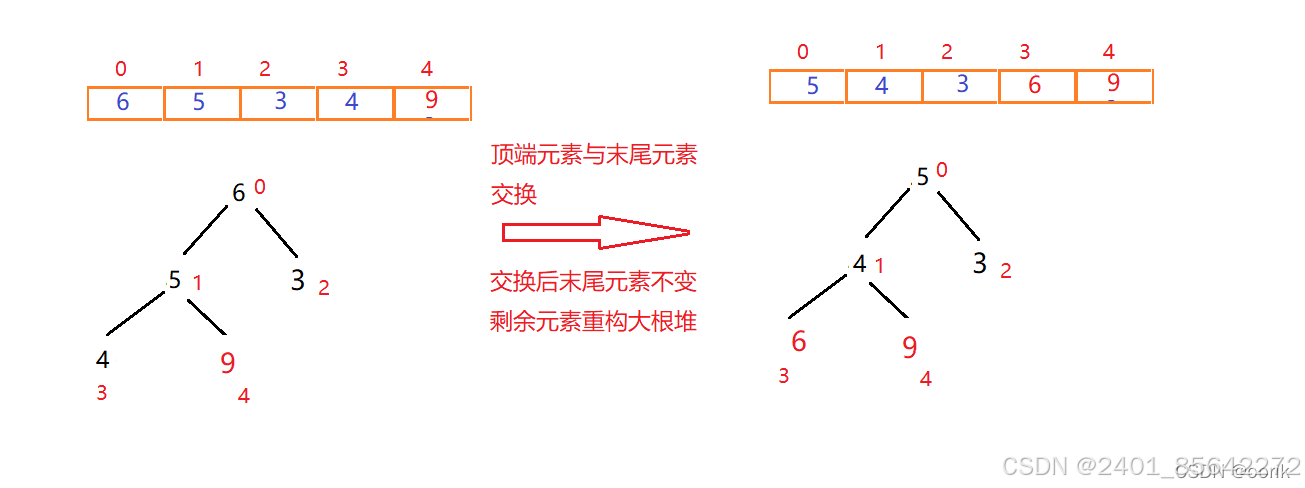
最终排序结果

 

小结：

堆排序算法的步骤：

1.把无序数组构建成二叉堆，把无序的一串数想象成一个堆，根据要求去从局部到整体构建一个大顶堆或者小顶堆，我们要的就是此时的堆顶元素

2.循环删除堆顶元素，移到集合尾部，调节堆产生新的堆顶。把堆顶元素和末尾元素交换就是把堆顶元素（数组首元素）换到了数组的末端

3.重现调整除了数组末端（已经确定顺序的元素）以外的元素，去构建堆，然后交换堆顶和当前末尾，构建，交换堆顶和当前末尾。

堆排序是不稳定的排序，空间复杂度为O(1)，平均时间复杂度为O(nlogn)，最坏情况下也稳定在 O(nlogn)。

void HeapAdjust(int* arr, int start, int end)
{
	int tmp = arr[start];
	for (int i = 2 * start + 1; i <= end; i = i * 2 + 1)
	{
		if (i < end&& arr[i] < arr[i + 1])//有右孩子并且左孩子小于右孩子
		{
			i++;
		}//i一定是左右孩子的最大值
		if (arr[i] > tmp)
		{
			arr[start] = arr[i];
			start = i;
		}
		else
		{
			break;
		}
	}
	arr[start] = tmp;
}
void HeapSort(int* arr, int len)
{
	//第一次建立大根堆，从后往前依次调整
	for(int i=(len-1-1)/2;i>=0;i--)
	{
		HeapAdjust(arr, i, len - 1);
	}
	//每次将根和待排序的最后一次交换，然后在调整
	int tmp;
	for (int i = 0; i < len - 1; i++)
	{
		tmp = arr[0];
		arr[0] = arr[len - 1-i];
		arr[len - 1 - i] = tmp;
		HeapAdjust(arr, 0, len - 1-i- 1);
	}
}
int main()
{
	int arr[] = { 9,5,6,3,5,3,1,0,96,66 };
	HeapSort(arr, sizeof(arr) / sizeof(arr[0]));
	printf("排序后为:");
	for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++)
	{
		printf("%d ", arr[i]);
	}
	return 0;
}

小根堆

void FF(vector<int>& nums, int start, int end)//构建最小堆
{
	int i = start, j = 2*i+1;
	int tmp = nums[i];
	while (j<=end)
	{
		if (j < end&& nums[j] > nums[j + 1]) j += 1;
		if (tmp <= nums[j])break;
		nums[i] = nums[j];
		i = j;
		j = i * 2 + 1;
	}
	nums[i] = tmp;
}
void SortFF(vector<int>&nums, int n)//堆排序
{
	//if ( nums.size()==0||n < 2)return;
	int pos = (((n - 1) - 1) / 2);
	while (pos >= 0)//从下往上局部，最后整体去调整成小顶堆
	{
		FF(nums, pos,n - 1);
		pos-=1;
	}
	//调整完了此时这个二叉堆最上面就是最小的数
	//在数组里就是一顿调整之后，第一个元素是最小的
 
	pos = n - 1;//让pos指向数组最后一个位置
	while (pos > 0)
	{
		swap(nums[0], nums[pos]);//交换第一个元素和pos指向的位置第一次完了之后，最小元素就在数组最后
		pos-=1;    //让pos指向数组往前一个位置，相当于最后一个元素是最小的已经确认
		FF(nums,0,pos);//那么就是开始重新调整除过已经确认元素剩下那一段数组元素
		                 //这下又把这一段数组里面最小的放在堆顶
		                 //再次进入循环，去交换位置	                
	}
}
 
int main()
{
	vector<int>vv{53,17,78,9,45,65,87,23};
	
	SortFF(vv,vv.size());
	for (auto const& x : vv) {
		cout << x << " ";
	}
	return 0;
}