无向图-基本操作函数（建立，广度遍历，深度遍历，邻接表表示）_一个连通分量的广度遍历的代码-优快云博客

本文链接：https://blog.youkuaiyun.com/2401_84247760/article/details/138821925

给大家的福利

零基础入门

对于从来没有接触过网络安全的同学，我们帮你准备了详细的学习成长路线图。可以说是最科学最系统的学习路线，大家跟着这个大的方向学习准没问题。

同时每个成长路线对应的板块都有配套的视频提供：

在这里插入图片描述

因篇幅有限，仅展示部分资料

网络安全面试题

绿盟护网行动

还有大家最喜欢的黑客技术

网络安全源码合集+工具包

所有资料共282G，朋友们如果有需要全套《网络安全入门+黑客进阶学习资源包》，可以扫描下方二维码领取（如遇扫码问题，可以在评论区留言领取哦）~

网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。

需要这份系统化资料的朋友，可以点击这里获取

一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！

使用邻接矩阵时，比较方便，只需要遍历以当前结点的为头结点的单链表即可遍历完它的所有邻接点。邻接表方式减少了很多的空间使用。

代码：

//广度遍历功能实现函数 参数：图G 作用：宽度遍历
void BFSTraverse(Graph G)
{
	for (int i = 0;i<MaxVerNum;i++)//初始化访问标记数组
	{
		visited[i] = false;
	}
	for (int i = 0;i < G.vexnum;i++)//对每个连通分量进行遍历
	{
		if (!visited[i])BFS(G, i);
	}
}

3.深度遍历

【分析】

采用递归方式进行深度遍历。

代码：

//深度遍历功能实现函数 参数：图G 作用：深度遍历
void DFSTraverse(Graph G)
{
	for (int i = 0;i<MaxVerNum;i++)//初始化访问标记数组
	{
		visited[i] = false;
	}
	for (int i = 0;i < G.vexnum;i++)//对每个连通分量进行遍历
	{
		if (!visited[i])
		{
			DFS(G, i);cout << endl;
		}
	}
}

4.全部代码

/*
Project: 图-邻接表表示（无向图）
Date:    2019/02/16
Author:  Frank Yu
基本操作函数:
InitGraph(Graph &G)             初始化函数 参数：图G 作用：初始化图的邻接表等
InsertNode(Graph &G,VexType v)  插入点函数 参数：图G,顶点v 作用：在图G中插入顶点v,即改变顶点表
InsertEdge(Graph &G,VexType v,VexType w) 插入边函数 参数：图G,某边两端点v和w 作用：在图G两点v,w之间加入边，即改变边表
BFS(Graph G, int start) 广度遍历函数 参数：图G,开始结点下标start 作用：广度遍历
DFS(Graph G, int start) 深度遍历函数（递归形式）参数：图G,开始结点下标start 作用：深度遍历
功能实现函数：
CreateGraph(Graph &G) 创建图功能实现函数 参数：图G，调用InsertNode等函数 作用：创建图
BFSTraverse(Graph G)  广度遍历功能实现函数 参数：图G 作用：宽度遍历
DFSTraverse(Graph G)  深度遍历功能实现函数 参数：图G 作用：深度遍历
*/
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<string>
#include<set>
#include<list>
#include<queue>
#include<vector>
#include<map>
#include<iterator>
#include<algorithm>
#include<iostream>
#define MaxVerNum 100 //顶点最大数目值
#define VexType char //顶点数据类型
#define EdgeType int //边数据类型,无向图时邻接矩阵对称，有权值时表示权值，没有时1连0不连
using namespace std;
//边表数据结构
typedef struct ArcNode
{
	int adj;//该弧所指向的顶点下标
	struct ArcNode *next;//指向下一条弧的指针
};
//顶点表数据结构
typedef struct VNode
{
	VexType data;//数据域
	ArcNode *first;//第一条依附该顶点的指针
}AdjList[MaxVerNum];
//图的数据结构
typedef struct Graph
{
	AdjList vertices;//邻接表
	int vexnum, arcnum;//顶点数、边数
}Graph;
//*********************************************基本操作函数*****************************************//
//初始化函数 参数：图G 作用：初始化图的邻接表等
void InitGraph(Graph &G)
{
	for (int i = 0;i < MaxVerNum;i++)//初始化邻接表
	{
		G.vertices[i].data = '#';
		G.vertices[i].first = NULL;
	}
	G.arcnum = G.vexnum = 0;          //初始化顶点数、边数
}
//插入点函数 参数：图G,顶点v 作用：在图G中插入顶点v,即改变顶点表
bool InsertNode(Graph &G, VexType v)
{
	if (G.vexnum < MaxVerNum)
	{
		G.vertices[G.vexnum++].data = v;
		return true;
	}
	return false;
}
//插入边函数 参数：图G,某边两端点v和w 作用：在图G两点v,w之间加入边，即改变边表
bool InsertEdge(Graph &G, VexType v, VexType w)
{
	int p1, p2;//v,w两点下标
	p1 = p2 = -1;//初始化
	for (int i = 0;i<G.vexnum;i++)//寻找顶点下标
	{
		if (G.vertices[i].data == v)p1 = i;
        if (G.vertices[i].data == w)p2 = i;
	}
	if (-1 != p1&&-1 != p2)//两点均可在图中找到
	{
		ArcNode* e1, *e2;
		e1 = (ArcNode*)malloc(sizeof(ArcNode));
		(*e1).adj = p1;
		e2 = (ArcNode*)malloc(sizeof(ArcNode));
		(*e2).adj = p2;
		//头插
		(*e1).next = G.vertices[p2].first;
		G.vertices[p2].first = e1;
		(*e2).next = G.vertices[p1].first;
		G.vertices[p1].first = e2;
		G.arcnum++;
		return true;
	}
	return false;
}
bool visited[MaxVerNum];//访问标记数组，用于遍历时的标记
//广度遍历函数 参数：图G,开始结点下标start 作用：广度遍历
void BFS(Graph G, int start)
{
	queue<int> Q;//辅助队列
	cout << G.vertices[start].data;//访问结点
	visited[start] = true;
	Q.push(start);//入队
	while (!Q.empty())//队列非空
	{
		int v = Q.front();//得到队头元素
		Q.pop();//出队
		ArcNode *e1 = G.vertices[v].first;
		while (e1->next)
		{
			if (!visited[e1->adj]) 
			{
			    cout << "->";
				cout << G.vertices[e1->adj].data;//访问结点
				visited[e1->adj] = true;
				Q.push(e1->adj);//入队
			}
				e1 = e1->next;
		}
	}//while
	cout << endl;
}
//深度遍历函数（递归形式）参数：图G,开始结点下标start 作用：深度遍历
void DFS(Graph G, int start)
{
	cout << G.vertices[start].data;//访问
	visited[start] = true;
	ArcNode *e1 = G.vertices[start].first;
	do
	{
	 if (!visited[e1->adj])//未访问
	 {
		cout << "->";
		DFS(G, e1->adj);//递归深度遍历
	 }
	 e1 = e1->next;
	} while (e1->next);
}
//**********************************************功能实现函数*****************************************//
//打印图的邻接表
void PrintAdj(Graph G)
{
	for (int i = 0;i < G.vexnum;i++)
	{
		cout << i<<" "<<G.vertices[i].data << " ";
		if (G.vertices[i].first)
		{
			ArcNode *p = G.vertices[i].first;
			while (p->next) 
			{

				cout << " "<<p->adj;
				p = p->next;
			}
			cout << " " << p->adj;
		}
		cout << endl;
	}
}
//创建图功能实现函数 参数：图G，调用InsertNode等函数 作用：创建图
void CreateGraph(Graph &G)
{
	VexType v, w;
	int vn, an;//顶点数，边数
	cout << "请输入顶点数目:" << endl;
	cin >> vn;
	cout << "请输入边数目:" << endl;
	cin >> an;
	cout << "请输入所有顶点名称:" << endl;
	for (int i = 0;i<vn;i++)
	{


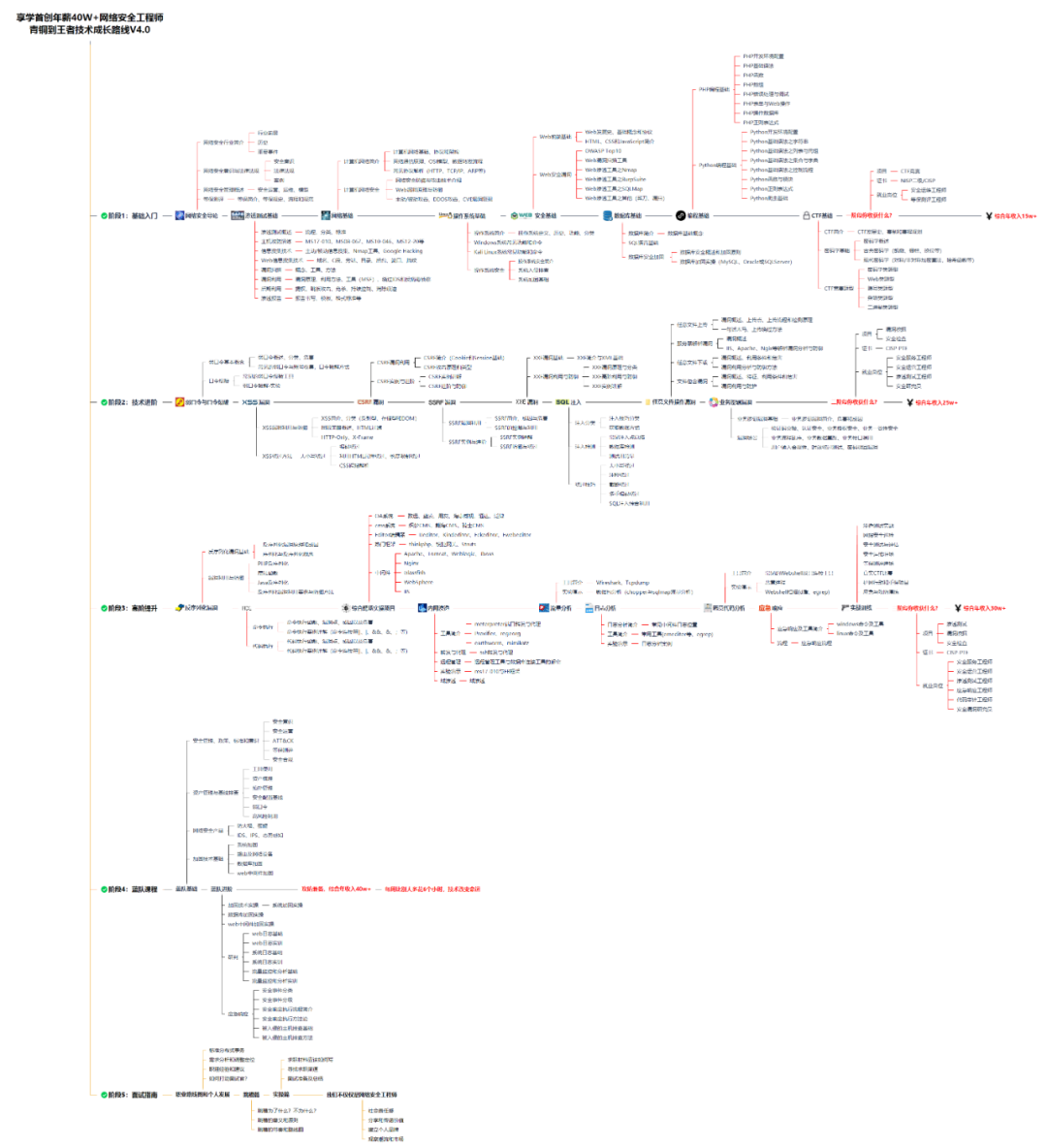
### 一、网安学习成长路线图


网安所有方向的技术点做的整理，形成各个领域的知识点汇总，它的用处就在于，你可以按照上面的知识点去找对应的学习资源，保证自己学得较为全面。  
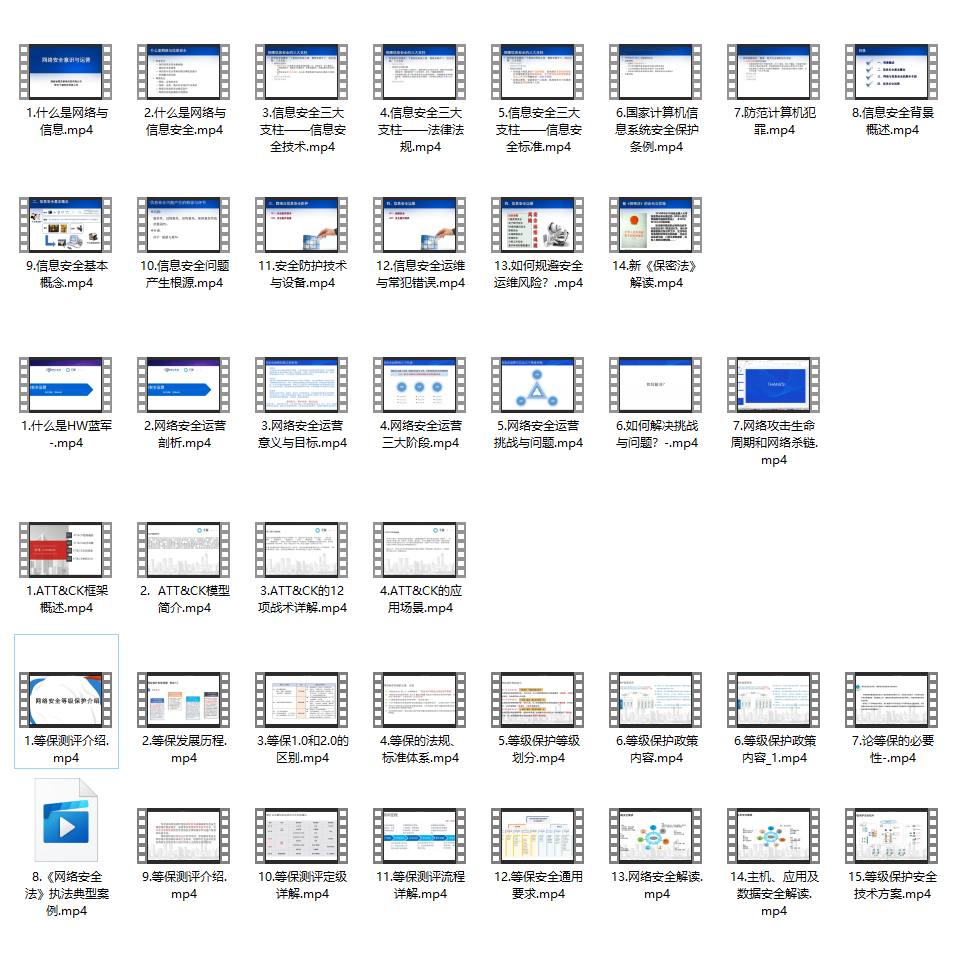
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/aa7be04dc8684d7ea43acc0151aebbf1.png)


### 二、网安视频合集


观看零基础学习视频，看视频学习是最快捷也是最有效果的方式，跟着视频中老师的思路，从基础到深入，还是很容易入门的。  
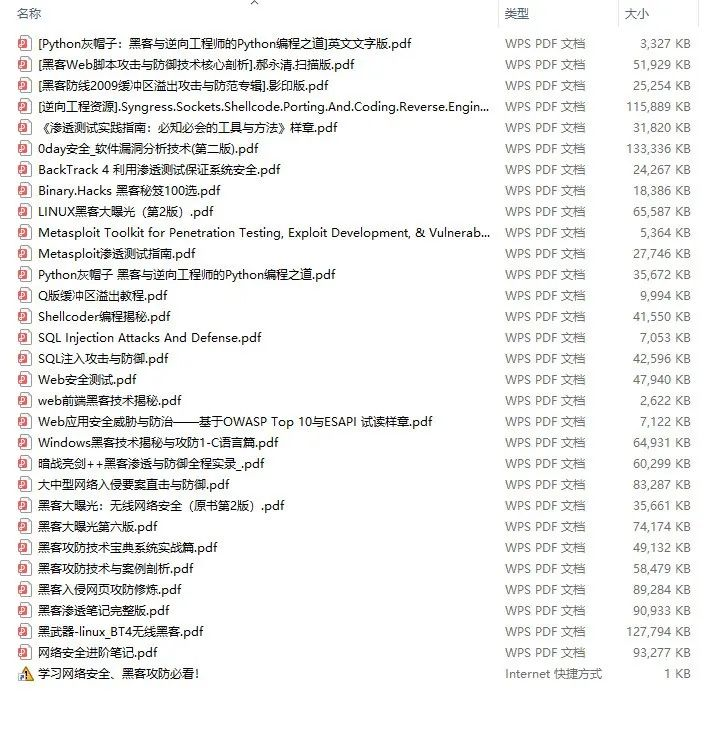
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/f0aeee2eec7a48f4ad7d083932cb095d.png)


### 三、精品网安学习书籍


当我学到一定基础，有自己的理解能力的时候，会去阅读一些前辈整理的书籍或者手写的笔记资料，这些笔记详细记载了他们对一些技术点的理解，这些理解是比较独到，可以学到不一样的思路。  
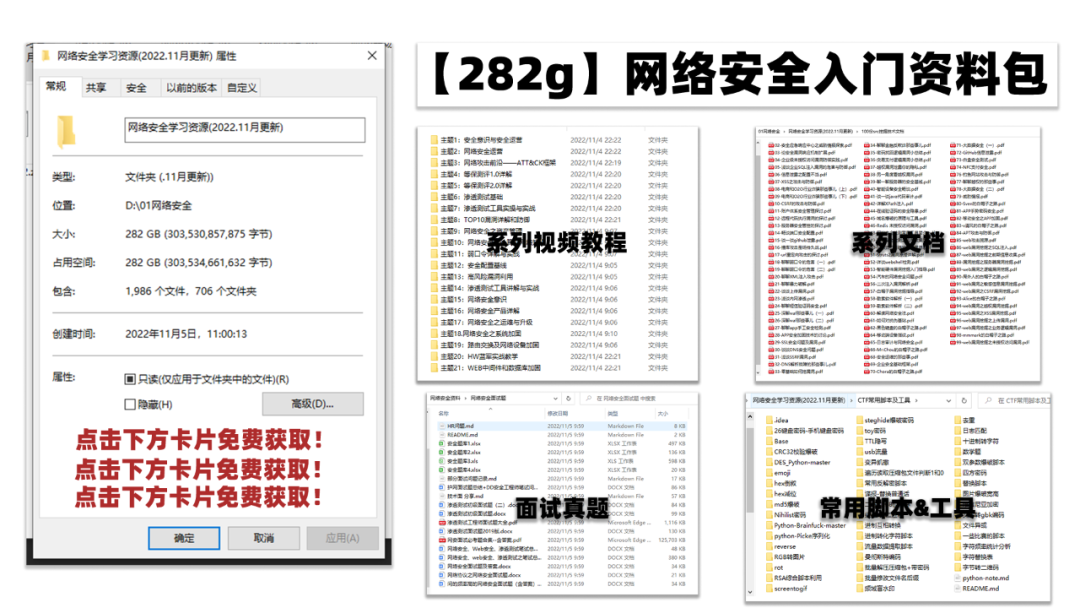
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/078ea1d4cda342f496f9276a4cda5fcf.png)


### 四、网络安全源码合集+工具包


光学理论是没用的，要学会跟着一起敲，要动手实操，才能将自己的所学运用到实际当中去，这时候可以搞点实战案例来学习。  
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/e54c0bac8f3049928b488dc1e5080fc5.png)


### 五、网络安全面试题


最后就是大家最关心的网络安全面试题板块  
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/15c1192cad414044b4dd41f3df44433d.png)![在这里插入图片描述](https://img-blog.csdnimg.cn/b07abbfab1fd4edc800d7db3eabb956e.png)  



**网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。**

**[需要这份系统化资料的朋友，可以点击这里获取](https://bbs.youkuaiyun.com/forums/4f45ff00ff254613a03fab5e56a57acb)**

**一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！**