跑步——百度之星2024

一、题目

1.题目这里

二、所用知识

1. 求1到n连续数列的lcm
2. 快速幂
3. 欧拉筛
4. 贡献法（决定能否a出来的重要因素）

三、代码讲解

1.首先要明确，两个人相互打招呼的次数怎么算，lcm / i - lcm / j
意思是两个人跑的圈数相减，不会的自己画画图想想，很好想的。

2.其次讲解最这道题用的贡献法是什么

long long t = lcm * inv[i] % mod;
res = (res + t * (n - 2 * i + 1) % mod +mod)%mod;
这个n - 2 * i + 1是怎么来的呢？
我们要知道，假设我们不使用贡献法，那么res是什么情况表示呢
其实，就是每个点的跑圈数相互做差。
如图：
圈中的序号是lcm/i，就是到结束时的圈数


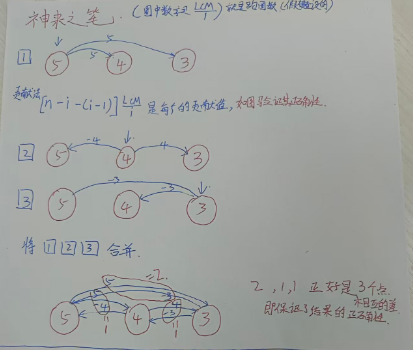
这道题用的贡献法说实话我没有用数学推出来，但是用画图说明了公式的正确性，记住以后会用就行。

为什么写纸上，因为作者不会LaTeX，正在学。

四、代码展示

写的有些唐了，但是思路很清晰，每一步都能知道在干什么。

#include<iostream>
#include<vector>
#include<cmath>
#define int long long //下面的long long 是因为原来没写，后来懒得改了。
using namespace std;
const int mod = 998244353;
const int MAXN = 1e7 + 1;
int n;
long long inv[MAXN], vis[MAXN];
long long qmi(long long a, long long b) {
    long long ans = 1;
    while (b) {
        if (b & 1) ans = (ans * a) % mod;
        a = (a * a) % mod;
        b >>= 1;
    }
    return ans;
}
signed main()
{
    ios_base::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    inv[1] = 1;
    cin >> n;
    for (int i = 2; i <= n; i++) {
        inv[i] = (long long)(mod - mod / i) * (inv[mod % i]) % mod;
    }

    vector<long long>prime;
    for (int i = 2; i <= n; i++) {
        if (!vis[i]) {
            prime.push_back(i);
        }
        for (int j = 0; j < prime.size() && i * prime[j] <= n; j++) {
            vis[i * prime[j]] = 1;
            if (i % prime[j] == 0) break;
        }
    }
    //求lcm
    long long lcm = 1;
    for (auto x : prime) {
        lcm = lcm * qmi(x, (long long)(log2(n) / log2(x))) % mod;
    }
    long long res = 0;
    for (int i = 1; i <= n; i++) {
        long long t = lcm * inv[i] % mod;
        res = (res + t * (n - 2 * i + 1) % mod +mod)%mod;
    }
    res%=mod;
    cout << res << '\n';
    return 0;
}

总得来说，这道题挺好的，考察很全面，知道那个贡献法结论后会很好写。