先自我介绍一下,小编浙江大学毕业,去过华为、字节跳动等大厂,目前阿里P7
深知大多数程序员,想要提升技能,往往是自己摸索成长,但自己不成体系的自学效果低效又漫长,而且极易碰到天花板技术停滞不前!
因此收集整理了一份《2024年最新网络安全全套学习资料》,初衷也很简单,就是希望能够帮助到想自学提升又不知道该从何学起的朋友。
既有适合小白学习的零基础资料,也有适合3年以上经验的小伙伴深入学习提升的进阶课程,涵盖了95%以上网络安全知识点,真正体系化!
由于文件比较多,这里只是将部分目录截图出来,全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频,并且后续会持续更新
如果你需要这些资料,可以添加V获取:vip204888 (备注网络安全)

正文
一. 树的简介
1. 概念
树(Tree) 是非线性结构的典型代表。在树型数据结构中,数据元素之间存在一对多的关系。在数据结构中,对树的定义是:树是由n(n>0)个有限结点组成一个具有层次关系的集合。当n=0时,称为空树。
之所以把这些由层次关系的结点集合称之为树,主要是因为其在形状上看起来特别像一棵倒挂的树,即树根朝上,树叶朝下。首先壹哥给出树结构所具备的特点:
(1). 树有且仅有一个特定的根(Root)结点。
(2). 除了根结点,其余每个结点都有且只有一个直接前驱,这个前驱结点叫父结点.
(3). 树的每个结点都可以有多个后继,叫做子结点。没有后继的结点称为叶子结点。有父结点,也有子结点,这样的结点被称为中间结点或分支结点。
(4). 除了根结点,其余结点可分为m(m>0)个互不相交的有限集合。其中每一个集合本身又是一棵树,称为子树。
但是,如果产生子树相交的情况,就不符合树结构的定义,也就不属于树了。比如下图:
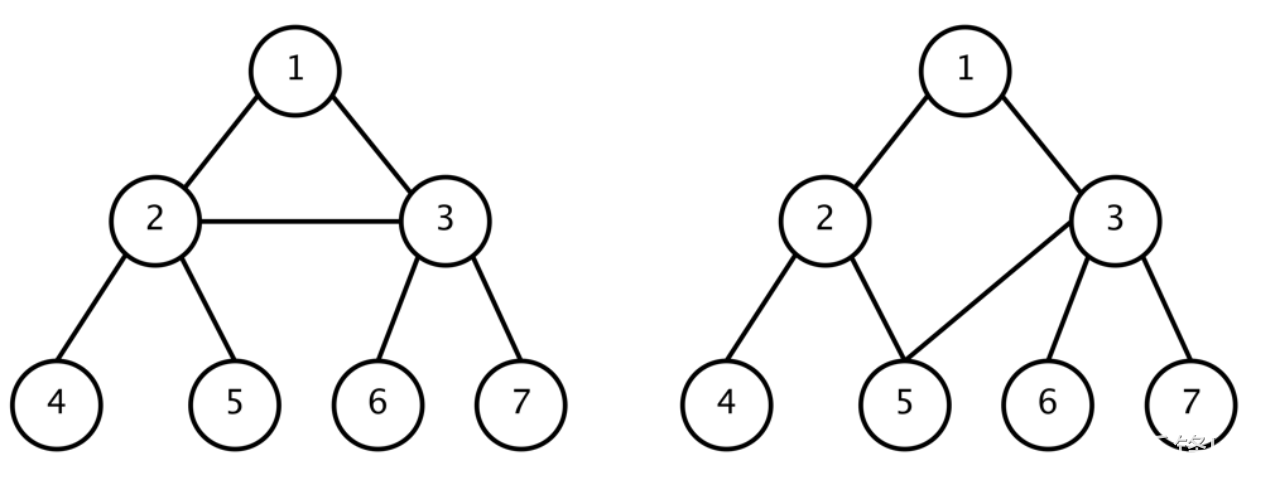
如上两图所示,左图中②和③有相交,右图中结点②和节点③均与节点⑤相连,这两种情况下都不能称之为树。
2. 基本术语
2.1 树的高度和深度
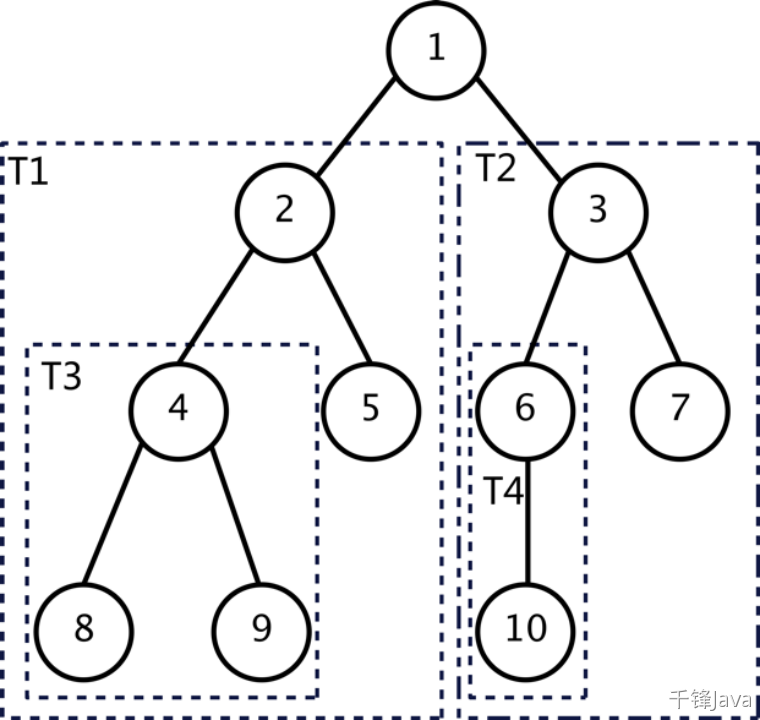
树的最大层级数,被称为树的高度或深度。我们通过图例说明如下:
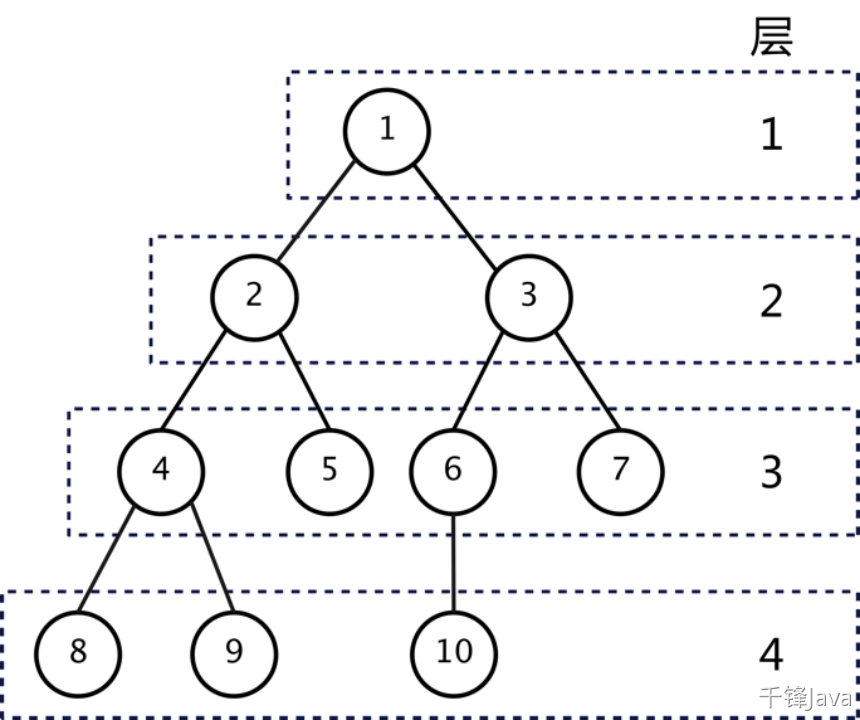
如上图所示,该树的高度是4,深度为4。根结点在第1层,结点8、9、10位于第4层。
备注:托马斯·科尔曼等人所著的《算法导论》一书中,树的高度是从“0”开始计数的,在本篇文章中,我们遵照惯例,树的高度是从“1”开始计数。
2.2 结点关系
具有同一父结点的结点互相称为兄弟结点。比如,上文图例所示中:结点2和3,结点4和5,结点6和7,结点8和9彼此是兄弟结点。
2.3 树的度数
特别的,我们把:一个结点的子结点的个数称为该结点的度数。度为0的结点就是叶子结点,而度不为0的结点就是分支结点。同时,我们还规定:一棵树的度指的是该树中结点的最大度数。比如,上文所示图例中:结点2、3、4的度为2,结点6的度为1,结点5、7、8、9、10的度为0。这棵树的度为2。
3. 树的分类
根据度的大小,我们可以将树可以分为二叉树和多路树。堆也属于一种多路树结构,另外根据度的大小,堆也分为二叉堆和多叉堆。具体的逻辑关系如下图所示:
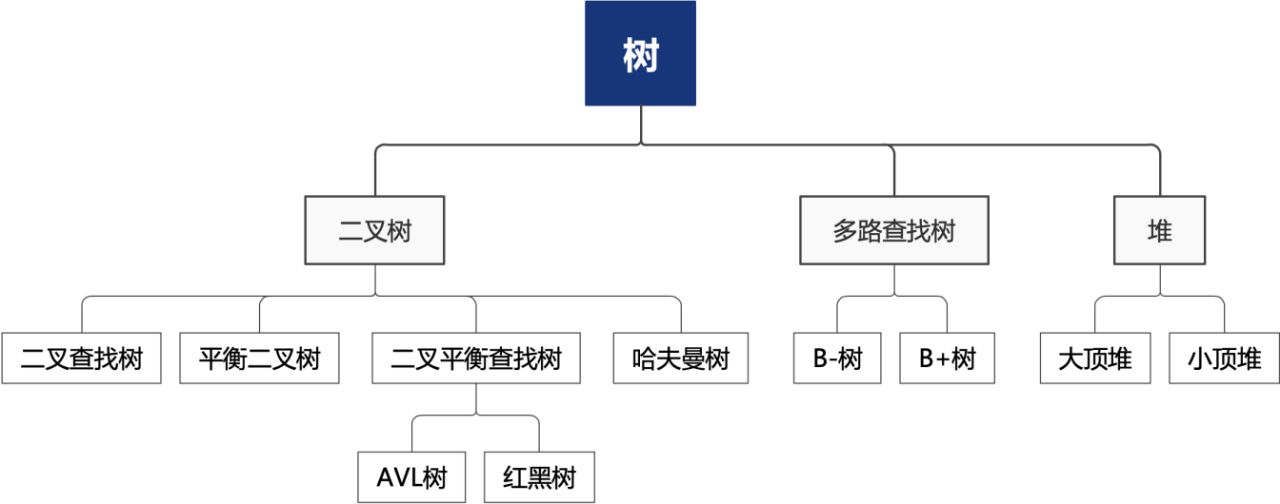
在如上的示例图中,给出了树型数据结构所涉及的常见的分类种类,在后续的文章中,我们会逐渐学习到,大家稍安勿躁,接下来让我们先从二叉树开始学起。
二. 二叉树
1. 概念
二叉树(Binary Tree) 是树的一种常见形式。二叉树的任意结点最多可以有两个子结点,也可以只有一个或者没有子结点。因此二叉树的度数一定小于等于2。二叉树结点的两个子结点,一个被称为左子结点,一个被称为右子结点。二叉树严格区分左右子结点,两个子结点的顺序是固定的,即使只有一棵子树也要区分左右。
如果我们把二叉树继续进行分类,就会衍生出满二叉树和完全二叉树。
- 满二叉树:满二叉树是一种理想状态。二叉树的所有非叶子结点都存在左右子结点,每个非叶子结点的度都是2,并且所有叶子结点都在同一层上,那么这个树就是满二叉树。
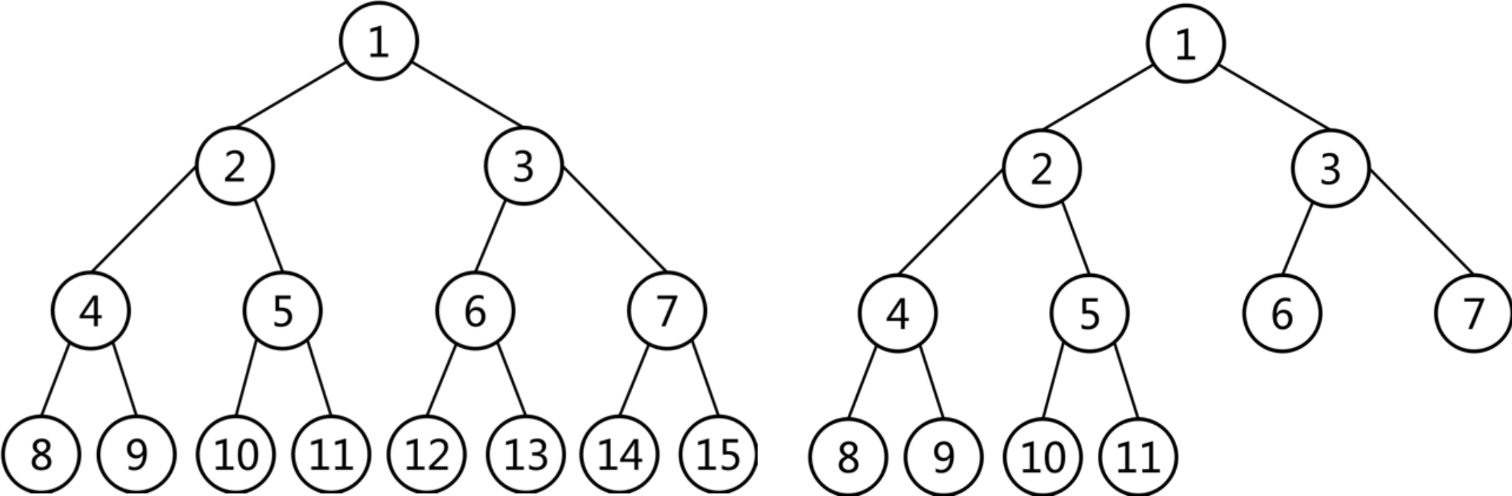
如上图所示: 左图中,所有非叶子结点都存在左右子结点,每个非叶子结点的度都是2,同时所有叶子结点均在同一层,符合满二叉树的定义,所以左图是满二叉树。右图中,虽然每个非叶子结点都有左右子结点,且每个非叶子结点的度都是2,但所有叶子结点并不在同一层,因此不属于满二叉树。由此,我们 可以知道,判断一棵二叉树是否是满二叉树,有三个条件:
- 每个非叶子结点都存在左右2个子结点
- 每个非叶子结点的度都是2
- 所有叶子结点均在同一层
以上三个条件,实际前两个条件描述的是同一回事。
- 完全二叉树:如果二叉树中除去最后一层结点为满二叉树,且最后一层的结点依次从左到右分布,则此二叉树被称为完全二叉树。
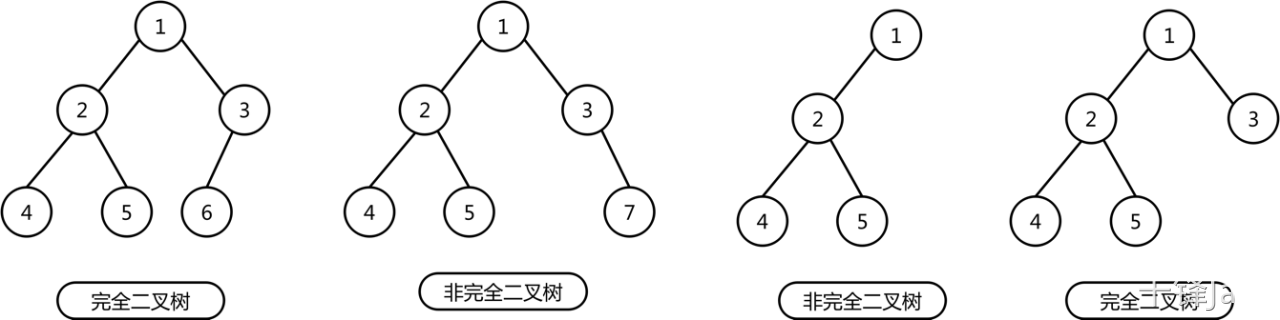
如上图所示,结合完全二叉树的定义,可以知道完全二叉树需要满足两个条件:
- 除最后一层外为满二叉树;
- 最后一层的结点依次从左至右,中间不能有缺失。
2. 性质
二叉树的性质,也是二叉树有关的一些结论,所谓结论,就是指这些设计到二叉树相关的特性的内容,可以直接作为结果或者结论进行引用。我们依然分类进行描述:
2.1 普通二叉树的性质
- 第i层最多可以有2 i-1 个结点:根据结论,我们可以验证二叉树第1层最多有1个结点,第2层最多有2个结点,第3层最多有4个结点,依次类推。当然,需要注意的是,此处说的是最多,并不是一定会有,要区分清楚。
- 若二叉树深度为k,则二叉树最多有2 k -1个结点:该结论也可以通过举例验证,二叉树的深度为1时,结点最多就1个;深度为2时,结点最多有3个;深度为3时,结点最多为7个。依次类推,均符合该结论公式。
- 若叶子结点数为n0,度为2的结点数为n2,则n0=n2+1:该结论也可以用另外一句话表述,即叶子结点数比度为2的结点多1个。
2.2 满二叉树的性质
满二叉树是特殊的二叉树,因此所有的普通二叉树的性质满二叉树都满足。除此之外,满二叉树特有的性质有:
- 满二叉树中第i层一定有2 i-1 个结点。
- 深度为k的满二叉树一定有2 k -1个结点,且一定有2 k-1 个叶子结点。
- 具有n个结点的满二叉树的深度为log 2 (n+1) 。
2.3 完全二叉树的性质
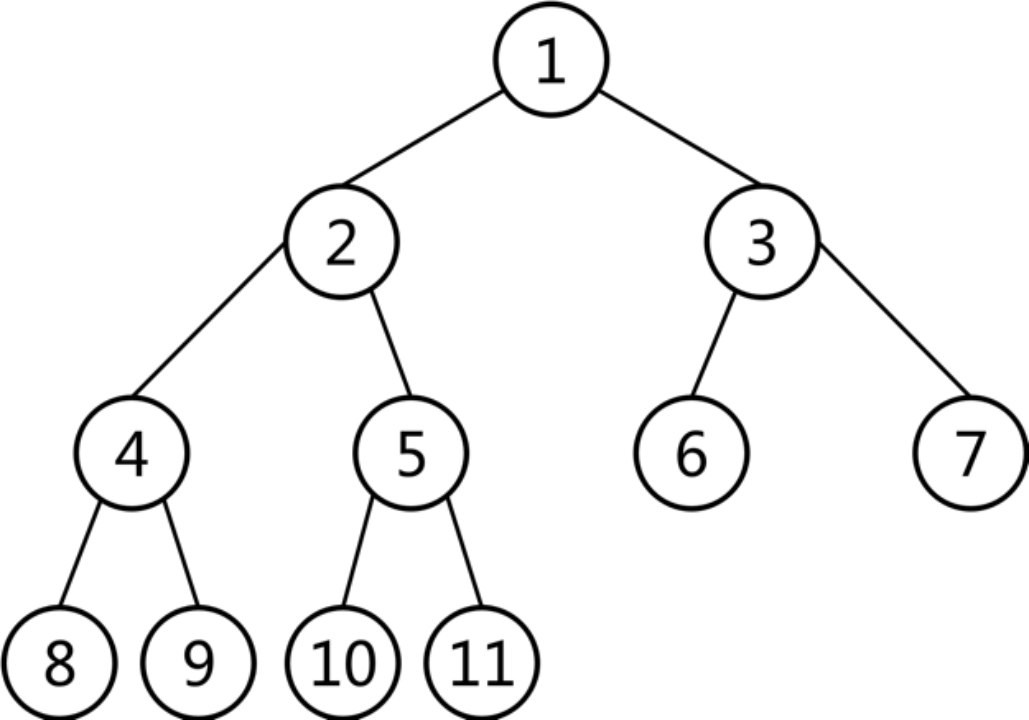
如上图所展示的是一棵完全二叉树,为了方便区分该二叉树的每一个结点,我们其将含有的结点按照层次从左到右依次标号,依次为1-11。若根据该规则,则对于任意一个结点i,完全二叉树具有以下结论:
- 若i>1,则i结点的父结点的编号是i/2(向下取整) 。比如:i=5结点,其父结点编号为2,满足结论。
- 若2i>n(n为总结点的个数),则结点i肯定没有左叶子结点,否则其左子结点是结点2i。
- 若2i+1>n,则结点i肯定没有右子结点;否则右子结点是结点2i+1。
- 完全二叉树只能有0个或1个度为1的结点,叶子结点数比度为2的结点数多1个。
总结: 对于普通二叉树,满二叉树,以及完全二叉树的特点和其所具有的性质,在使用时最简单的方式是通过画图例的方式进行验证,当然如果我们能把上文中列出的所有性质公式都记住自然是最好的。
3. 二叉树的存储
在前面的文章中,我们已经学习过数组和链表,此处刚好可以使用这种结构对二叉树的结点进行存储。因此,二叉树的存储一共有两种方式,分别是:顺序存储、链式存储。
3.1 顺序存储(数组)
所谓的顺序存储,指的是使用数组存储的二叉树。
我们在使用数组存储时,会按照层级顺序把二叉树的结点放到数组中对应的位置上。如果某一个结点的左子结点或右子结点空缺,则数组的相应位置也要空出来。对于一个稀疏的二叉树(子结点不满)来说,用顺序存储是非常浪费空间的。所以二叉树的顺序存储一般只适用于完全二叉树,或者说完全二叉树才适合使用顺序表存储。当顺序存储普通二叉树时,需要提前将普通二叉树转化为完全二叉树。
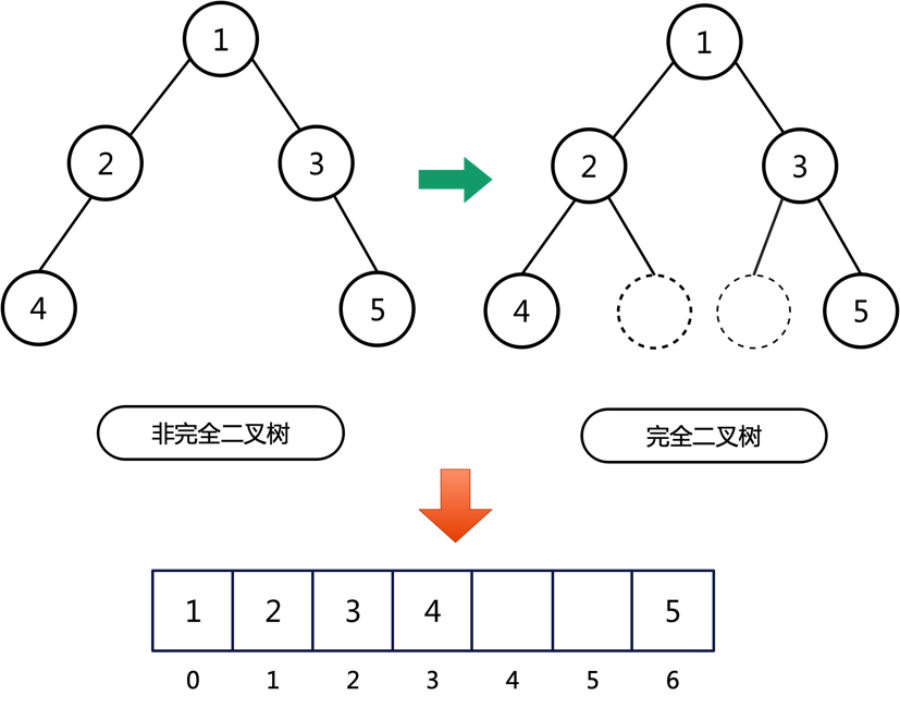
如上图所示,给定的二叉树是一棵普通的二叉树。若使用数组进行存储,首先需要将该二叉树补充调整为一棵完全二叉树如上右图所示,需要添加的两个结点使用虚线表示(不存储具体数据,空余),然后再使用数组存储该完全二叉树。可以看到,上图的数组中,下标4和下标5位置空余,原因是两位位置恰好对应的是补充的两个结点。
给大家的福利
零基础入门
对于从来没有接触过网络安全的同学,我们帮你准备了详细的学习成长路线图。可以说是最科学最系统的学习路线,大家跟着这个大的方向学习准没问题。

同时每个成长路线对应的板块都有配套的视频提供:

因篇幅有限,仅展示部分资料
网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。
需要这份系统化的资料的朋友,可以添加V获取:vip204888 (备注网络安全)

一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!
体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。**
需要这份系统化的资料的朋友,可以添加V获取:vip204888 (备注网络安全)
[外链图片转存中…(img-pON0voIE-1713615838294)]
一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!
























 918
918

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








