坚持每日Codeforces三题挑战：Day 6 - 题目详解（2025-06-10，难度：800,1400,1400）-优快云博客

void solve() {
    int n;
    std::cin >> n;

    std::string s;
    std::cin >> s;

    char mn = 'z';
    for (char& c : s) {
        mn = std::min(mn, c);
    }

    for (int i = n - 1; i >= 0; i--) {
        if (s[i] == mn) {
            std::cout << s[i] << s.substr(0, i) + s.substr(i + 1) << "\n";
            return;
        }
    }
}

题目二:

Problem - C - Codeforces

题目大意:

现在给你n个数字ki，每个数字k表示直线y = kx的斜率。

再给你m个数对{ai, bi, ci}，每个数对表示一个抛物线y = a * (x ^ 2) + b * x + c。

现在对于给出的每一条抛物线，你都需要在给出的直线中找到一条，保证这条直线与这个抛物线不相交也不相切，如果没有这样的直线，输出NO。

解题思路:

既不相交也不相切，也就是说只有没有交点，也就是说联立两个方程得到的方程a * (x ^ 2) + (b - k) x + c = 0没有解。对于这个二次一次方程来说，判别式是(b - k) ^ 2 - 4 * a * c，要使得方程没有解，也就是判别式小于0。

好了，数学推导大致到这里。

现在我们的目标就是找出这样的k，使得判别式尽可能的小于0，也就是让|b - k|尽可能接近0，k的值尽可能接近b。

思路就变成了，每次查找一个最接近b的k，然后判断判别式此刻的k是否可以满足判别式小于0。

实际操作中，可以用二分查找快速查找这样的k。

代码(C++):

void solve() {
    int n, m;
    std::cin >> n >> m;

    std::vector<int> k(n);
    for (int i = 0; i < n; i++) {
        std::cin >> k[i];
    }
    //排序,二分查找
    std::sort(k.begin(), k.end());

    while (m--) {
        //后面乘法会涉及到溢出,这里直接用i64快捷
        i64 a, b, c;
        std::cin >> a >> b >> c;
        
        //查找接近b的k,这里会有两个值k[i - 1]和k[i]都接近b,不需要判断哪个最接近
        //都判断一遍即可
        int i = std::lower_bound(k.begin(), k.end(), b) - k.begin();
        i64 r = 4 * a * c;
        if (i < n) {
            i64 x = k[i] - b;
            if (x * x < r) {
                std::cout << "Yes\n" << k[i] << "\n";
                continue;
            }
        }
        if (i > 0) {
            i64 x = k[i - 1] - b;
            if (x * x < r) {
                std::cout << "Yes\n" << k[i - 1] << "\n";
                continue;
            }
        }
        std::cout << "No\n";
    }
}

题目三:

Problem - C - Codeforces

题目大意:

给你三个数字b, c, d，让你在[0, 2 ^ 61]这个范围内找出一个数字a，满足：

(a | b) - (a & c) = d

如果不存在这样的a，输出-1即可

解题思路:

我们要注意的关键一点是：我们只需要对二进制下的每一位单独计算即可，因为二进制下的每一位互不影响。

因为是减法，不会产生进位，对于每一个二进制位，我们把(a | b) ，(a & c)当成整体。

那么对于某一二进制位，只有可能是1 - 0 = 1, 0 - 0 = 0, 1 - 1 = 0。（不存在0 - 1 = -1的情况）

我们可以根据(a, b, c)的八种情况列举出d的对应情况如图（参考官方题解）：

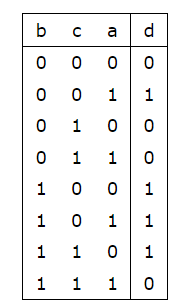
根据表可以发现，b, c, d为1, 0, 0和0，1，1的时候是不成立的。

实际代码实现的时候，因为我们只需要关注位数，那么我们只需要遍历从0到61，用三个变量来记录当前的位bit_b,bit_c,bit_d。

根据表来计算a：

对于每一个二进制位：

当bit_b和bit_c都为1的时候，a的对应位的值跟d的对应位的值相反。

其余时候a的值跟d的值相同。

代码(C++):

void solve() {
    i64 b, c, d;
    std::cin >> b >> c >> d;

    i64 a = 0, ok = 1, mask = 1;
    i64 bit_b, bit_c, bit_d;
    for (int i = 0; i < 62; i++) {
        bit_b = (b & mask ? 1 : 0);
        bit_c = (c & mask ? 1 : 0);
        bit_d = (d & mask ? 1 : 0);

        if ((bit_b && (!bit_c) && (!bit_d)) || (!bit_b && bit_c && bit_d)) {
            ok = 0;
            break;
        }
        
        if (bit_b && bit_c) {
            a += (1LL - bit_d) * mask;
        } else {
            a += bit_d * mask;
        }

        mask <<= 1;
    }

    if (ok) {
        std::cout << a << "\n";
    } else {
        std::cout << "-1\n";
    }
}