目录
1.栈
1.1栈的概念及结构
栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。
压栈:栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶。
出栈:栈的删除操作叫做出栈。出数据也在栈顶。
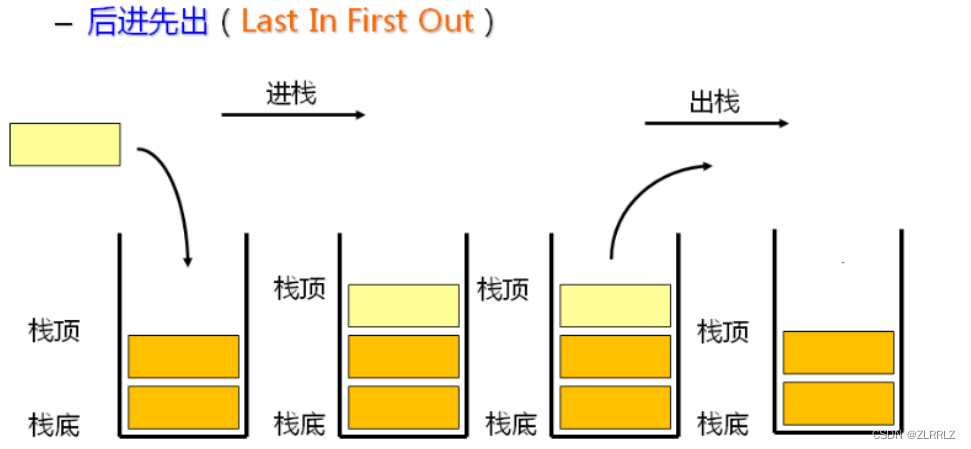
栈在逻辑上仍然是线性的,但是与顺序表、链表不同,栈只能在栈顶入数据,在栈底出数据,不能在任意位置进行操作,栈顶与栈底是根据功能命名的,没有严格规定首部是栈顶,尾部是栈底。
1.2栈的实现
1.2.2实现结构的选择
在数据结构之前的学习中,我们已经学习了链式与数组这两种存储的结构,栈的实现一般都可以使用数组或者链表实现。相对而言数组的结构实现更优一些。因为数组在尾上插入数据的 代价比较小。
a.数组
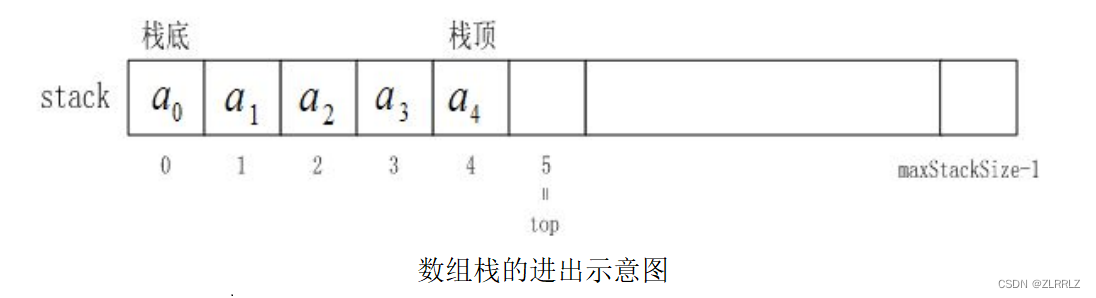
对于数组而言,如果我们将头部作为栈底,那么压栈出栈就需要挪动许多数据,算法复杂度为较大,因此我们一般将数组头部作为栈顶,尾部作为栈底.
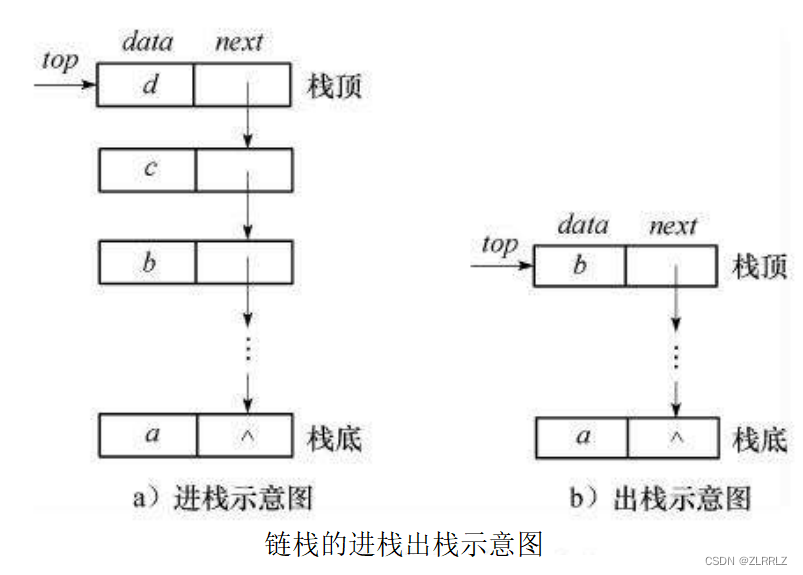
b.链表
与数组不同,对于单链表而言,如果我们将链表的尾部作为栈底,我们是无法直接访问链表尾部的,同时进行压栈、出栈时,我们还需要找到尾节点的前一个节点,这样使用链表构建栈就会相当麻烦,读者读到这里,可能会认为找前一个节点麻烦,这是由于单链表结构的固有缺陷导致的,那我们直接使用双向链表,不就好了吗?确实,找前一个节点不麻烦了,但是为了解决这个问题,使用了双向链表,那么我们每个节点就多出一个需要维护的节点,空间损耗就大了,而且找尾节点还是需要遍历的,总得来说,我们花费的代价就太大了。因此将链表的尾部作为栈底并不是一个明智的选择。因此我们还是使用单链表(不带头),只不过将单链表第一个有效节点处,作为栈顶。这样我们进行压栈、出栈就方便了。
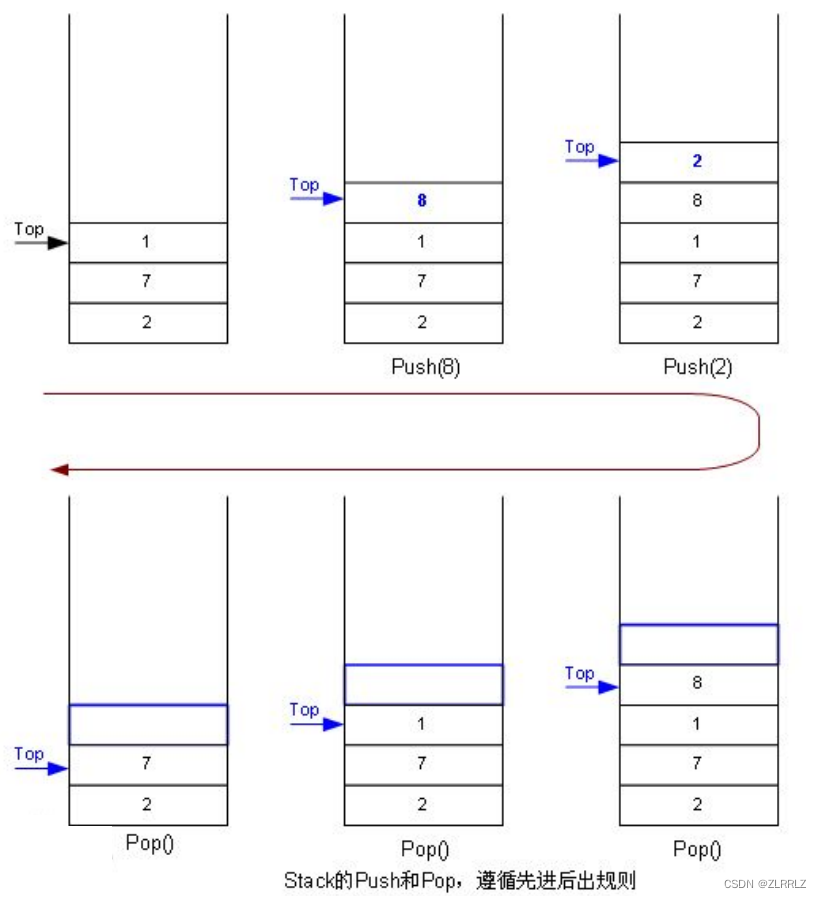
c.更优的选择
数组与链表两种结构看上去各有千秋,不过,实际上有数组去实现栈会更优一些。有的读者可能会认为如果是动态开辟数组的话,不是会有扩容上的消耗吗?同时不是还有将数据迁移到新的空间上的消耗吗?确实,如果仅看这些,按需申请的链表似乎更优一些,但是扩容调用的是系统上的资源,运行很快,并且一次扩容都是按倍扩,扩容的次数并不会很多,更重要的是数组的CPU的高速缓存更好(涉及知识点较多,这里便不展开了),因此,这里笔者主要使用数组来实现栈。
1.2.3实现结构
a.栈的结构体
静态的结构在实践用到的地方并不多,因此我们实现动态增长的栈。栈的结构体中,_a指向动态开辟的数组空间,_top用来指向栈顶元素或者栈顶元素的下一个位置,_capacity用来表示栈的容量
// 支持动态增长的栈
typedef int STDataType;
typedef struct Stack
{
STDataType* _a;
int _top; // 栈顶
int _capacity; // 容量
}Stack;b.栈的初始化
栈的初始化中,需要注意的是_top的初始值初始化为-1与初始化为0是截然不同的。我们的惯性思考会认为没有数据就是0,但是_top此处并不是单纯的表示数据个数的,我们知道数组能访问到最小下表是0,如果_top是表示指向栈顶数据的,那么当_top初始化为0,表示没有数据,当数组内有一个数据时,为了表示有一个数据,我们就将_top+1吗?这样似乎浪费空间了,因此如果_top是表示指向栈顶数据,我们就将_top初始化为-1,如果_top指向栈顶数据的下一个位置,我们就将_top始化为 0,这时的_top就还可以表示表示数组元素的个数了。笔者接下来实现栈的结构,_top指向栈顶元素的下一个位置。
// 初始化栈
void StackInit(Stack* ps)
{
assert(ps);
ps->_a = NULL;
// top指向栈顶数据的下一个位置
ps->_top = 0;
// top指向栈顶数据
//ps->_top = -1;
ps->_capacity = 0;
}c.栈的销毁
// 销毁栈
void StackDestroy(Stack* ps)
{
assert(ps);
free(ps->_a);
ps->_a = NULL;
ps->_capacity = ps->_top = 0;
}d.入栈
入栈之前,我们需要先判断数组的空间是否足够,如果不足,我们再扩容,因为_top指向的是栈顶元素的下一个数据,一次插入时的_top当前指向的位置就是要插入数据的位置。之后_top再加一。
// 入栈
void StackPush(Stack* ps, STDataType data)
{
assert(ps);
//扩容
if(ps->_capacity == ps->_top)
{
//对于第一次开辟空间,先初始化4个字节空间,之后每次扩容,扩大两倍
int newcapacity = ps->_capacity == 0 ? 4 : 2 * ps->_capacity;
STDataType* newnode = (STDataType*)realloc(ps->_a, newcapacity * sizeof(STDataType));
if (NULL == newnode)
{
perror("StackInit:realloc");
exit(1);
}
ps->_a = newnode;
//更新容量的记录值
ps->_capacity = newcapacity;
}
ps->_a[ps->_top] = data;
ps->_top++;
}
e.出栈
// 出栈
void StackPop(Stack* ps)
{
assert(ps);
assert(ps->_top > 0);
ps->_top--;
}f.获取栈顶元素
// 获取栈顶元素
STDataType StackTop(Stack* ps)
{
assert(ps);
assert(ps->_top > 0);
return ps->_a[ps->_top - 1];
}g.获取栈中有效元素个数
// 获取栈中有效元素个数
int StackSize(Stack* ps)
{
assert(ps);
return ps->_top;
}h.检测队列是否为空,如果为空返回非零结果,如果非空返回0
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
bool StackEmpty(Stack* ps)
{
assert(ps);
return ps->_top == 0;
}2.队列
2.1队列的概念及结构
队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出 FIFO(First In First Out) 入队列:进行插入操作的一端称为队尾 出队列:进行删除操作的一端称为队头
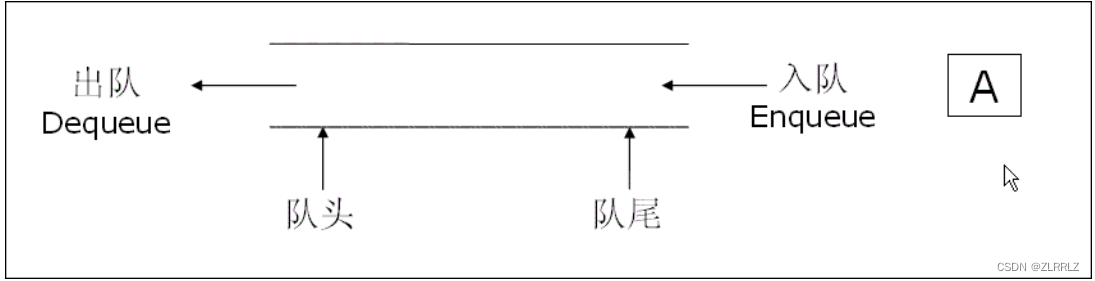
2.2队列的实现
2.2.1.实现结构的选择
队列也可以数组和链表的结构实现,使用链表的结构实现更优一些,因为如果使用数组的结构,出队列在数 组头上出数据时,就需要挪动数据,效率会比较低。
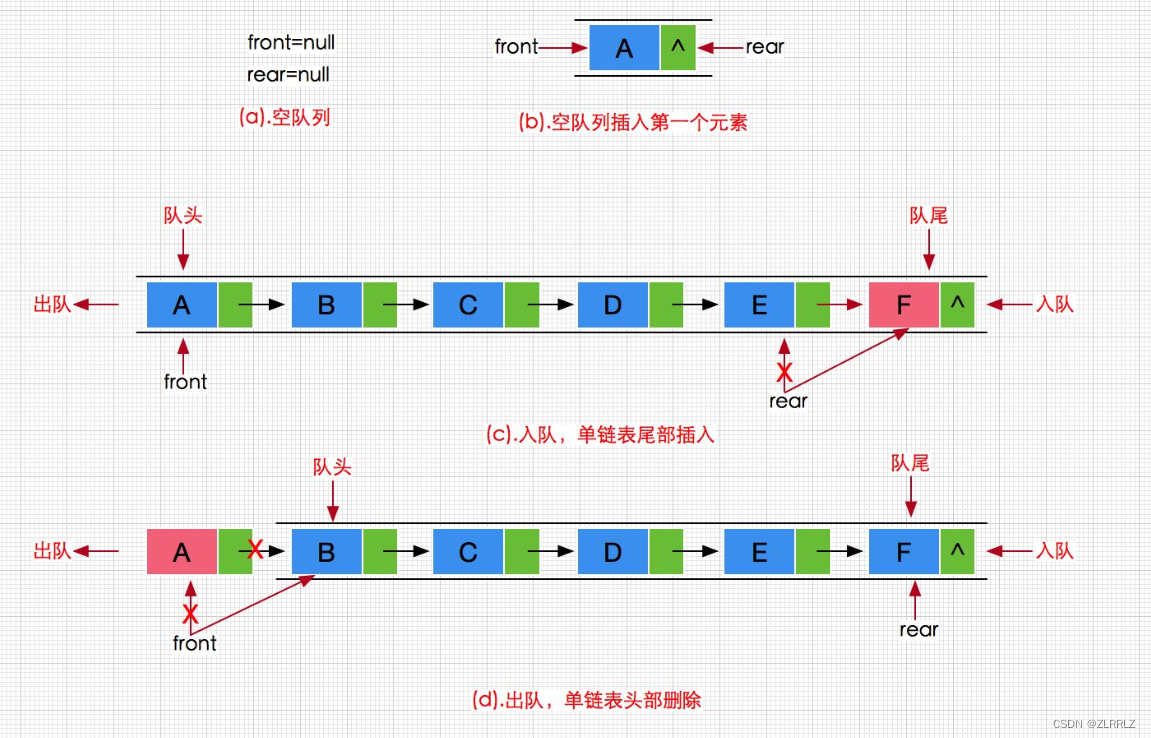
2.2.2.实现结构的选择
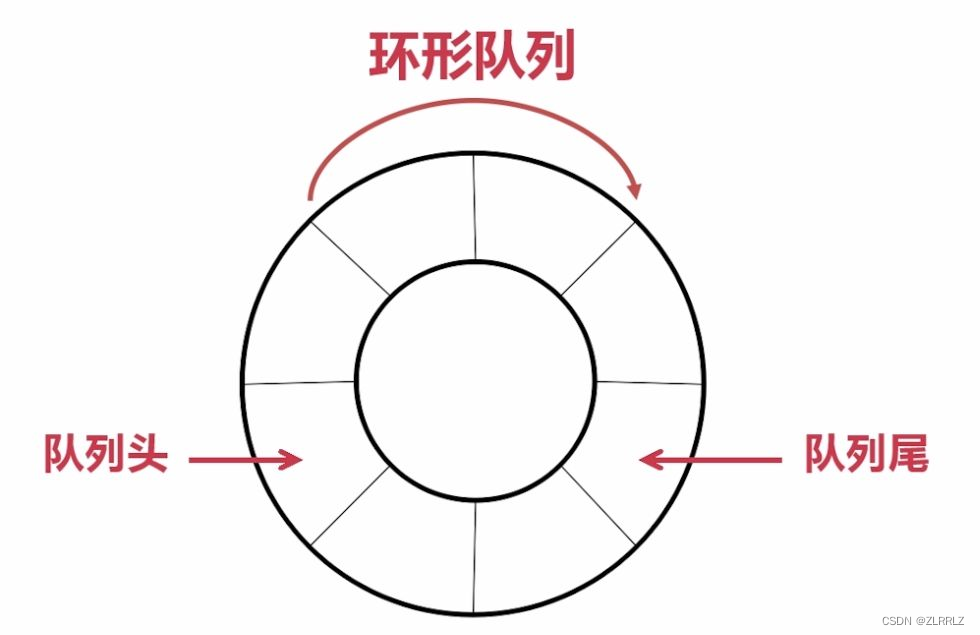
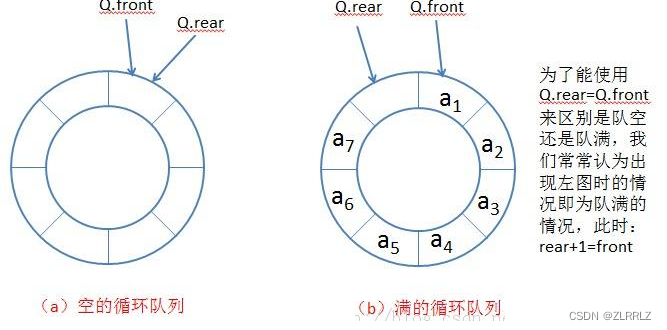
另外扩展了解一下,实际中我们有时还会使用一种队列叫循环队列。如操作系统课程讲解生产者消费者模型 时可以就会使用循环队列(涉及到许多其他知识,这里便不过多介绍)。环形队列可以使用数组实现,也可以使用循环链表实现。
a.单个队列节点的结构体
typedef int QDataType;
// 链式结构:表示队列
typedef struct QListNode
{
struct QListNode* _next;
QDataType _data;
}QNode;b.维护队列的结构体
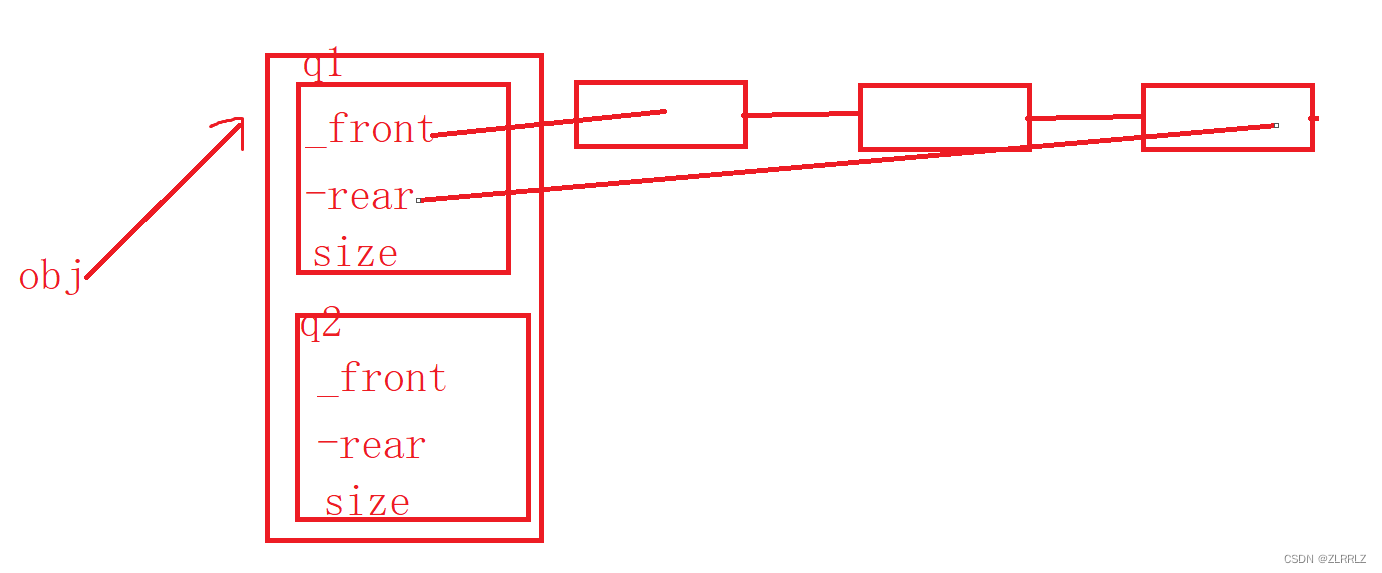
与栈不同,在实现队列时,以入队列为例,我们需要传尾指针,如果要改变尾节点还要传对应的二级指针,同时如果队列现在一个节点都没有,我们还需要传对应头指针的二级指针。总得来说,各种接口的使用似乎非常不便,针对这种问题,我们专门创建一个结构体去维护头指针与尾指针。调用接口时,我们只需要传入这个结构体的指针就可以了。这样我们就可以通过访问结构体来改变对应的头尾指针。此外加上_size记录数据个数

// 队列的结构
typedef struct Queue
{
QNode* _front;
QNode* _rear;
int _size;
}Queue;c.队列的初始化
传入专门维护的结构体初始化。
// 初始化队列
void QueueInit(Queue* q)
{
q->_front = NULL;
q->_rear = NULL;
q->_size = 0;
}d.销毁队列
循环遍历节点,挨个释放
// 销毁队列
void QueueDestroy(Queue* q)
{
assert(q);
QNode* cur = q->_front;
while(cur)
{
QNode* next = cur->_next;
free(cur);
cur = next;
}
q->_front = q->_rear = NULL;
q->_size = 0;
}e.队尾入队列
如果队列内没有节点时,在入队列时,还需要该表头结点。
// 队尾入队列
void QueuePush(Queue* q, QDataType data)
{
assert(q);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (NULL == newnode)
{
perror("QueuePush:malloc failed");
exit(1);
}
newnode->_data = data;
newnode->_next = NULL;
if (NULL == q->_rear)
{
q->_front = q->_rear = newnode;
}
else
{
q->_rear->_next = newnode;
q->_rear = newnode;
}
q->_size++;
}f.队头出队列
出队列之前需要判断是否队列中是否存在数据,没有数据,无法出数据。如果队列队列中只有一个数据,出完数据,还需要改变尾指针。
// 队头出队列
void QueuePop(Queue* q)
{
assert(q);
assert(q->_size);
QNode* next = q->_front->_next;
free(q->_front);
q->_front = next;
if (q->_size == 1)
{
q->_rear = NULL;
}
q->_size--;
}g.获取队列头部元素
首先判断头指针是否为空,不为空才可以获取头部元素。
// 获取队列头部元素
QDataType QueueFront(Queue* q)
{
assert(q);
assert(q->_front);
return q->_front->_data;
}h.获取队列队尾元素
首先判断尾指针是否为空,不为空才可以获取尾部元素。
// 获取队列队尾元素
QDataType QueueBack(Queue* q)
{
assert(q);
assert(q->_rear);
return q->_rear->_data;
}i.获取队列中有效元素个数
// 获取队列中有效元素个数
int QueueSize(Queue* q)
{
assert(q);
return q->_size;
}j.检测队列是否为空,如果为空返回非零结果,如果非空返回0
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
bool QueueEmpty(Queue* q)
{
assert(q);
return q->_size == 0;
}
3.栈和队列面试题
1. 括号匹配问题。OJ链接


这一道题,要求左括号与对应的右括号匹配,当取出字符串中的右括号时,需要与当前右括号的前面第一个左括号括号比对,如果是对应的左括号,则匹配成功,取下一个右括号,并且取前面第一个左括号匹配(已经匹配的左括号不再参与匹配)。我们发现我们总是需要取离右括号最近的左括号(相对其他左括号顺序靠后的元素)。匹配后,已匹配的括号不参加,下次匹配据需向“左找”。
因此根据题意,我们这里可以创建栈,循环遍历字符数组,如果当前是左括号,则入栈,如果是右括号,那么这时,我们就取栈顶的元素(由于栈是后入先出栈,因此栈顶的元素就是左边离右括号最近的左括号),与右括号匹配,如果匹配则,将匹配的左括号出栈,继续循环,如果不匹配,则结束遍历。

#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
#include<stdio.h>
// 支持动态增长的栈
typedef int STDataType;
typedef struct Stack
{
STDataType* _a;
int _top; // 栈顶
int _capacity; // 容量
}Stack;
// 初始化栈
void StackInit(Stack* ps)
{
ps->_a = NULL;
ps->_capacity = ps->_top = 0;
}
// 入栈
void StackPush(Stack* ps, STDataType data)
{
assert(ps);
if(ps->_capacity == ps->_top)
{
int newcapacity = ps->_capacity == 0 ? 4 : 2 * ps->_capacity;
STDataType* newnode = (STDataType*)realloc(ps->_a, newcapacity * sizeof(STDataType));
if (NULL == newnode)
{
perror("StackInit:realloc");
exit(1);
}
ps->_a = newnode;
ps->_capacity = newcapacity;
}
ps->_a[ps->_top] = data;
ps->_top++;
}
// 出栈
void StackPop(Stack* ps)
{
assert(ps);
assert(ps->_top > 0);
ps->_top--;
}
// 获取栈顶元素
STDataType StackTop(Stack* ps)
{
assert(ps);
assert(ps->_top > 0);
return ps->_a[ps->_top - 1];
}
// 获取栈中有效元素个数
int StackSize(Stack* ps)
{
assert(ps);
return ps->_top;
}
// 检测栈是否为空,如果为空返回0,如果不为空返回非零结果
bool StackEmpty(Stack* ps)
{
assert(ps);
return ps->_top;
}
// 销毁栈
void StackDestroy(Stack* ps)
{
assert(ps);
free(ps->_a);
ps->_a = NULL;
ps->_capacity = ps->_top = 0;
}
bool isValid(char* s)
{
Stack p;
StackInit(&p);
while(*s)
{
if(*s == '(' || *s == '{' || *s == '[')//左括号入栈
{
StackPush(&p,*s);
}
else
{
if(!StackEmpty(&p))//右括号入栈前不能没有左括号,否则一定会出现不匹配的情况
{
StackDestroy(&p);
return false;
}
char top = 0;
top = StackTop(&p);
if(top == '(' && *s != ')'||top == '{' && *s != '}'||top == '[' && *s != ']')//括号不匹配返回false
{
StackDestroy(&p);
return false;
}
StackPop(&p);//匹配成功,将匹配的左括号出栈
}
s++;//移动到下一个括号
}
int ret = !StackEmpty(&p);//判断栈内是否为空,为空说明存在未匹配的左括号
StackDestroy(&p);
return ret;
}2. 用队列实现栈。OJ链接

这一题,我们需要根据队列先进先出的性质实现栈后进先出的性质,题目给了我们两个队列,因此这题就是通过将数据在两个列类之间转移来完成的,问题的关键就在于如何转移数据。

如果说队列中已经有数据,为了出4,这是我们就可以将1、2、3入队列入到q2中,这时我们就可以出q1中的4,达到后进先出的效果,之后加入我们入栈5,6呢?我们又将5,6入到哪个队列中呢?
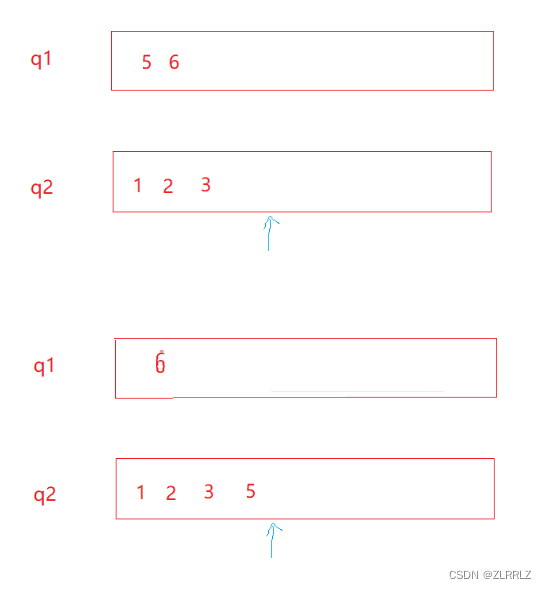
假如们入到 q1,中,这时如果我们将5入到q2,再出6,似乎没什么问题,那么这是如果我们不出6,我们还需要继续导入数据呢?

这是我们发现,面对两个都不为空的队列,我们再想入数据,我们必须先遍历已经存储的数据进行,判断当数据较多时,我们就会发现复杂度以及程序的逻辑性都不会太好。因此,为了避免这一混乱的情况发生,我们必须保证将数据入到不为空的队列,这样出数据将数据导到空队列中,出完数量后,就又保持两队列一空一不为空了。
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include"stdbool.h"
typedef int QDataType;
// 链式结构:表示队列
typedef struct QListNode
{
struct QListNode* _next;
QDataType _data;
}QNode;
// 队列的结构
typedef struct Queue
{
QNode* _front;
QNode* _rear;
int _size;
}Queue;
void QueueInit(Queue* q)
{
q->_front = NULL;
q->_rear = NULL;
q->_size = 0;
}
// 队尾入队列
void QueuePush(Queue* q, QDataType data)
{
assert(q);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (NULL == newnode)
{
perror("QueuePush:malloc failed");
exit(1);
}
newnode->_data = data;
newnode->_next = NULL;
if (0 == q->_size)
{
q->_front = q->_rear = newnode;
}
else
{
q->_rear->_next = newnode;
q->_rear = q->_rear->_next;
}
q->_size++;
}
// 队头出队列
void QueuePop(Queue* q)
{
assert(q);
assert(q->_size);
QNode* next = q->_front->_next;
free(q->_front);
q->_front = next;
if (q->_size == 1)
{
q->_rear = NULL;
}
q->_size--;
}
// 获取队列头部元素
QDataType QueueFront(Queue* q)
{
assert(q);
assert(q->_size);
return q->_front->_data;
}
// 获取队列队尾元素
QDataType QueueBack(Queue* q)
{
assert(q);
assert(q->_size);
return q->_rear->_data;
}
// 获取队列中有效元素个数
int QueueSize(Queue* q)
{
assert(q);
return q->_size;
}
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
bool QueueEmpty(Queue* q)
{
assert(q);
return q->_size == 0;
}
// 销毁队列
void QueueDestroy(Queue* q)
{
assert(q);
QNode* cur = q->_front;
while(cur)
{
QNode* next = cur->_next;
free(cur);
cur = next;
}
q->_front = q->_rear = NULL;
q->_size = 0;
}
typedef struct {
Queue q1;
Queue q2;
} MyStack;
MyStack* myStackCreate() {
MyStack*pst = (MyStack*)malloc(sizeof(MyStack));
//创建模拟的栈时,只能malloc动态创建,不能静态开辟,否则出了函数,开辟空间会被收回
//也不能使用static, 否则多次调用函数,值会一直保存,会出问题。
if(NULL == pst)
{
perror("malloc");
exit(1);
}
QueueInit(&pst->q1);
QueueInit(&pst->q2);
return pst;
}
void myStackPush(MyStack* obj, int x) {
if(!QueueEmpty(&obj->q1))
{
QueuePush(&obj->q1,x);
}
else
{
QueuePush(&obj->q2,x);
}
}
int myStackPop(MyStack* obj) {
//假设法
Queue* empty = &(obj->q1);
Queue* nonempty = &(obj->q2);
if(!QueueEmpty(&(obj->q1)))
{
nonempty = &(obj->q1);
empty = &(obj->q2);
}
//不为空的队列前size-1导走,删除最后一个就是栈顶数据
while(QueueSize(nonempty) > 1)
{
QueuePush(empty,QueueFront(nonempty));
QueuePop(nonempty);
}
int top = QueueFront(nonempty);
QueuePop(nonempty);
return top;
}
int myStackTop(MyStack* obj) {
if(!QueueEmpty(&(obj->q1)))
{
return QueueBack(&(obj->q1));
}
else
{
return QueueBack(&(obj->q2));
}
}
bool myStackEmpty(MyStack* obj) {
//两个队列都为空才是空
return QueueEmpty(&(obj->q1))&&QueueEmpty(&(obj->q2));
}
void myStackFree(MyStack* obj) {
QueueDestroy(&(obj->q1));
QueueDestroy(&(obj->q2));
free(obj);
}
/**
* Your MyStack struct will be instantiated and called as such:
* MyStack* obj = myStackCreate();
* myStackPush(obj, x);
* int param_2 = myStackPop(obj);
* int param_3 = myStackTop(obj);
* bool param_4 = myStackEmpty(obj);
* myStackFree(obj);
*/
需要注意的是最后销毁时,要先销毁队列对应的空间,在销毁存储两个队列指针的空间。
3. 用栈实现队列。OJ链接

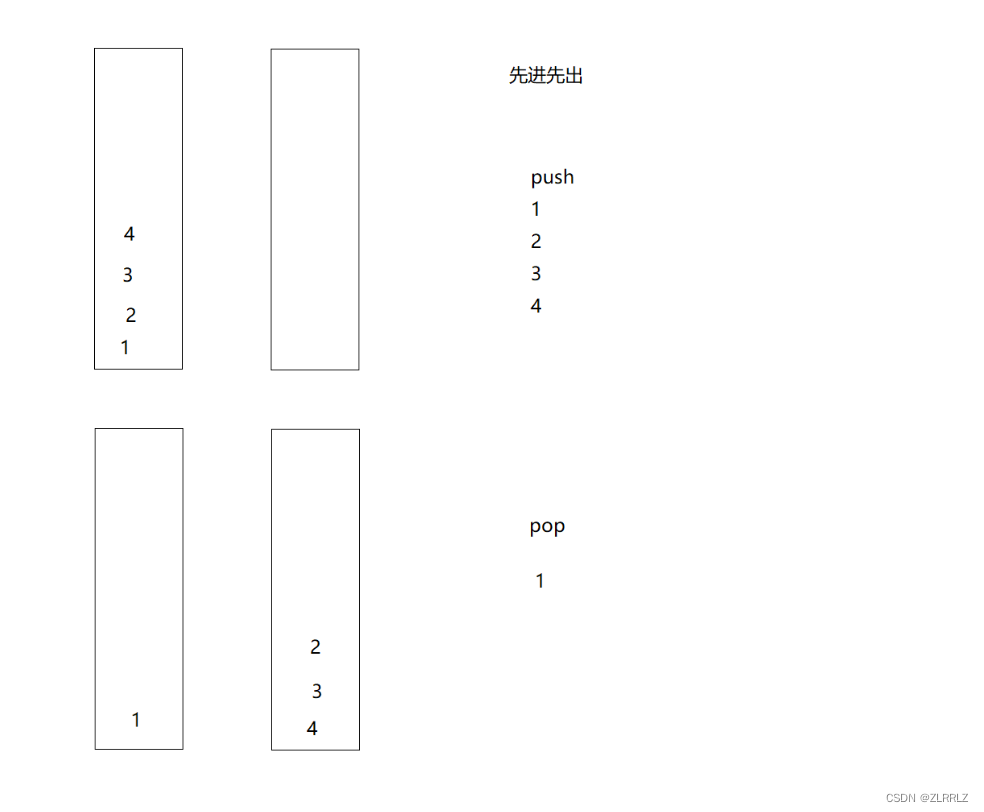
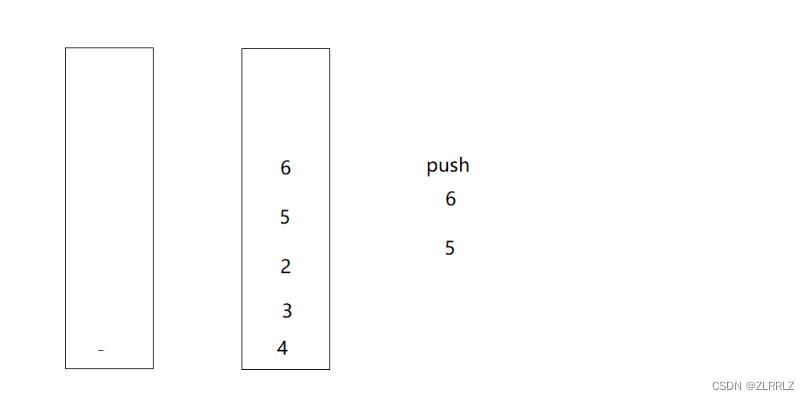
对于这一题,如果我们沿用用队列实现栈的思路,似乎也可以,我们将先将其他数据入到另一个栈中,再留下要出栈的数据出栈。但是我们要入栈时,我们不能在入到非空的栈中,因为这样,出数据的时候,顺序就完全乱了,对此,我们可以将原数据再倒回原数据中,再向非空栈中入数据。这样就没问题了,但是这样就比较麻烦了。
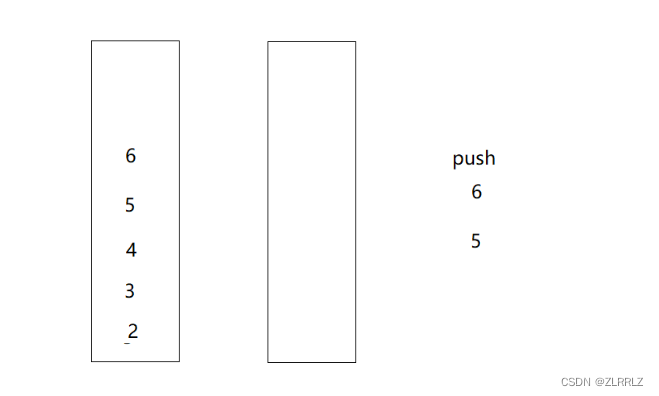
根据观察,我们发现其实在将数据到到空栈是,原数据顺序会倒过来,这是我们再出栈,就直接实现了先进先出的效果。
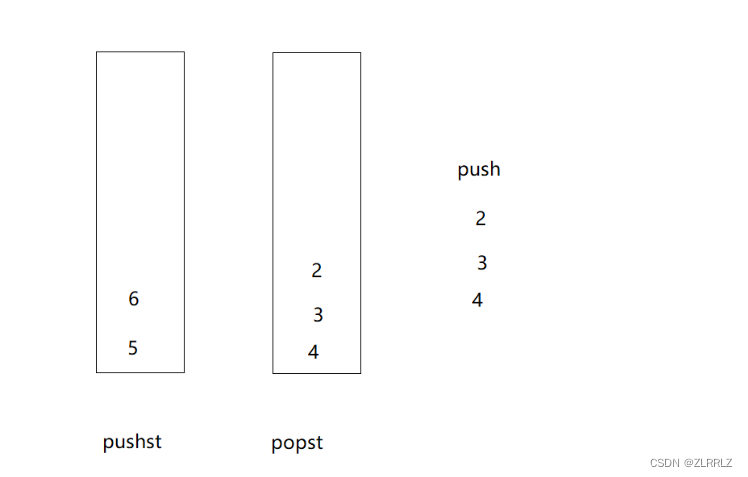
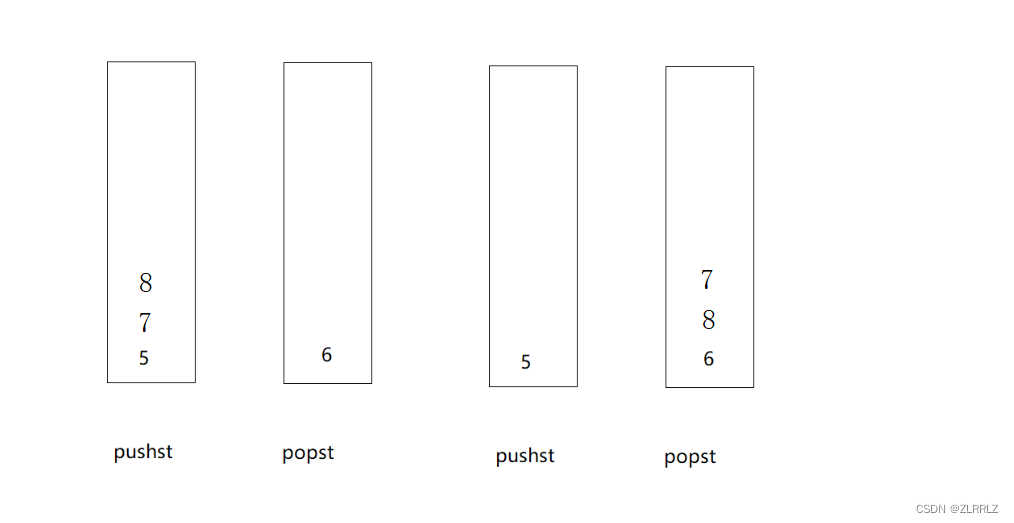
因此我们将两个栈分成一个专门出数据,一个专门入数据,当出数据栈popst为空,我们就将入数据栈pushst数据全部导到popst中(必须一次性将所有数据全部导入,否则顺序就乱了。)入数据时,直接往对应栈入就行了。
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
#include<stdio.h>
// 支持动态增长的栈
typedef int STDataType;
typedef struct Stack
{
STDataType* _a;
int _top; // 栈顶
int _capacity; // 容量
}Stack;
// 初始化栈
void StackInit(Stack* ps)
{
ps->_a = NULL;
ps->_capacity = ps->_top = 0;
}
// 入栈
void StackPush(Stack* ps, STDataType data)
{
assert(ps);
if(ps->_capacity == ps->_top)
{
int newcapacity = ps->_capacity == 0 ? 4 : 2 * ps->_capacity;
STDataType* newnode = (STDataType*)realloc(ps->_a, newcapacity * sizeof(STDataType));
if (NULL == newnode)
{
perror("StackInit:realloc");
exit(1);
}
ps->_a = newnode;
ps->_capacity = newcapacity;
}
ps->_a[ps->_top] = data;
ps->_top++;
}
// 出栈
void StackPop(Stack* ps)
{
assert(ps);
assert(ps->_top > 0);
ps->_top--;
}
// 获取栈顶元素
STDataType StackTop(Stack* ps)
{
assert(ps);
assert(ps->_top > 0);
return ps->_a[ps->_top - 1];
}
// 获取栈中有效元素个数
int StackSize(Stack* ps)
{
assert(ps);
return ps->_top;
}
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
bool StackEmpty(Stack* ps)
{
assert(ps);
return ps->_top == 0;
}
// 销毁栈
void StackDestroy(Stack* ps)
{
assert(ps);
free(ps->_a);
ps->_a = NULL;
ps->_capacity = ps->_top = 0;
}
typedef struct {
Stack pushst;
Stack popst;
} MyQueue;
MyQueue* myQueueCreate() {
MyQueue* q1 = (MyQueue*)malloc(sizeof(MyQueue));
StackInit(&q1->pushst);
StackInit(&q1->popst);
return q1;
}
void myQueuePush(MyQueue* obj, int x) {
//实现入队列数据
StackPush(&obj->pushst,x);
}
int myQueuePeek(MyQueue* obj) {
if(StackEmpty(&obj->popst))
{
//倒数据
//实现出队列数据
while(!StackEmpty(&obj->pushst))//专门出数据的栈为空,就先导入一下数据
{
StackPush(&obj->popst,StackTop(&obj->pushst));
StackPop(&obj->pushst);
}
}
return StackTop(&obj->popst);
}
int myQueuePop(MyQueue* obj) {
//出队列队头数据
int front = myQueuePeek(obj);
StackPop(&obj->popst);
return front;
}
bool myQueueEmpty(MyQueue* obj) {
//两个栈都为空,队列才为空
return StackEmpty(&obj->pushst)&&StackEmpty(&obj->popst);
}
void myQueueFree(MyQueue* obj) {
//先释放对应栈空间,再释放队列对应空间
StackDestroy(&obj->pushst);
StackDestroy(&obj->popst);
free(obj);
}
/**
* Your MyQueue struct will be instantiated and called as such:
* MyQueue* obj = myQueueCreate();
* myQueuePush(obj, x);
* int param_2 = myQueuePop(obj);
* int param_3 = myQueuePeek(obj);
* bool param_4 = myQueueEmpty(obj);
* myQueueFree(obj);
*/4. 设计循环队列。OJ链接

这道题目的意思就是队列的的空间大小是固定的,这些空间可以重复使用,看到这一题的循环结构,也许有的读者会想到链表,认为链表的结构完成这一题会比数组简单,但是实际上并不是这样的,笔者这里先以数组完成这题,链表的不便后文讲解。
首先假设要插入的空间K是4,这是如果我们开辟4个空间,head、tail都初始化为0,push一个数据,tail++,pop一个数据,head++,当tail、head值大于K,通过%K,实现回环,这样head == tail时,就代表数组为空的情况了,但是,我们发现如果数组满时也会出现head == tail,这就是我们说的假溢出的情况了。

为了解决这个问题,笔者有两种方法,一种是创建size专门记录数组元素个数;还有一种是多开一个空间。笔者接下来重点介绍第二种(对于这类问题一些官方解答更喜欢用第二种方法)。
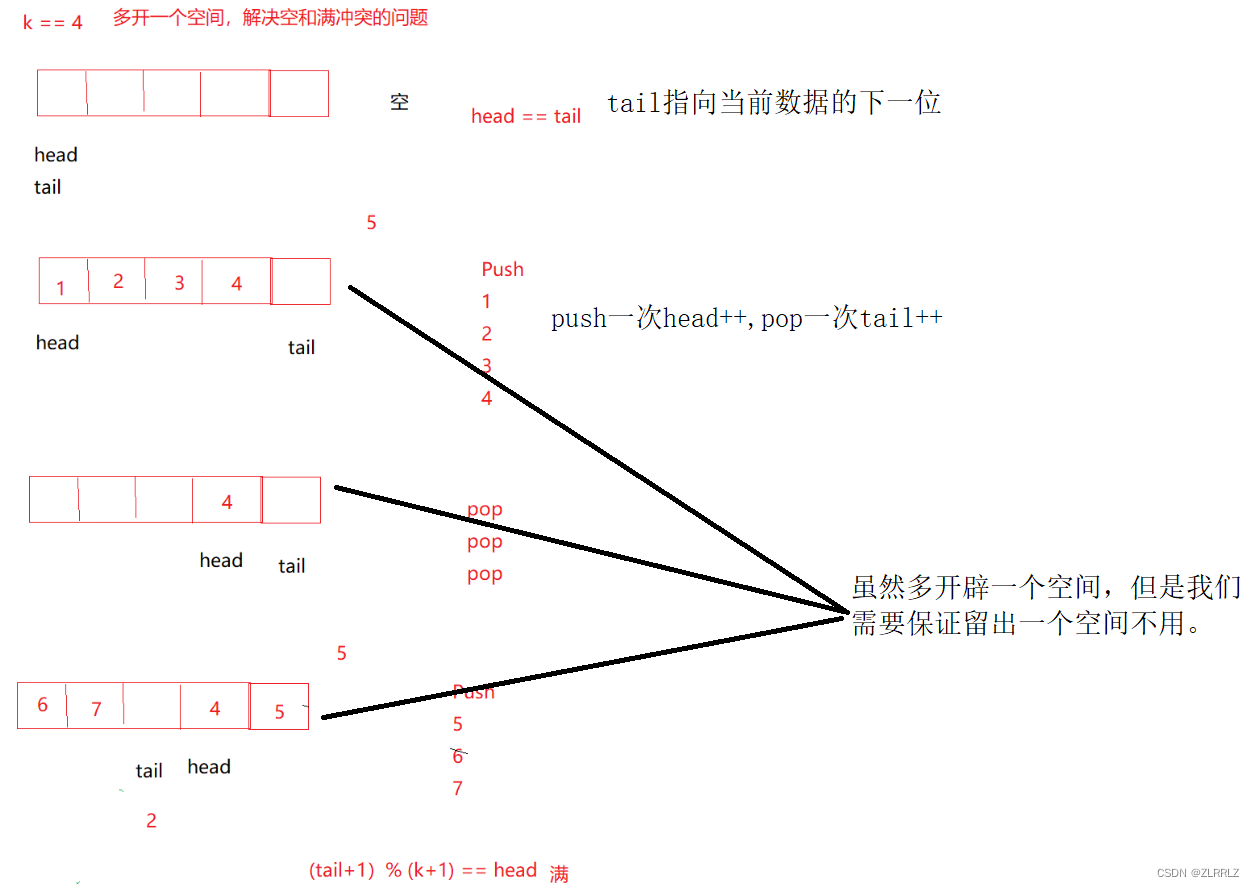
如上图,其他不变,只是我们判断数组满到条件变成了(tail+1)%(k+1) == head;这是为什么呢?我们知道,head是指向队列的头,tail指向尾的下一位,因为我们多开了一个空间,并且是按序的空出空间,因此,当数组满时,尾的空间后面就是空空间,tail指向它,这时如果tail再向前走一步,就与head相等,不过这时,为了避免出现越界的情况,tail+1需要%(K+1),这就相当于tail+1>5时,tail+1-5,tail回到数组开头,同时数组越界的情况是相对与数组总长的,因此这里是%(k+1)不是%k.

typedef struct {//创建结构体存储需要用到的值方便维护
int k;
int head;
int tail;
int* a;
} MyCircularQueue;
MyCircularQueue* myCircularQueueCreate(int k) {//初始化结构体
MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
obj->a = (int*)malloc((k + 1) * sizeof(int));
obj->head = 0;
obj->tail = 0;
obj->k = k;
return obj;
}
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
return obj->head == obj->tail;//head == tail为空
}
bool myCircularQueueIsFull(MyCircularQueue* obj) {
return (obj->tail + 1)%(obj->k + 1) == obj->head;//(tail + 1)%(k + 1) == head 为满
}
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
if(myCircularQueueIsFull(obj))
{
return false;
}
else
{
obj->a[obj->tail] = value;
obj->tail = (obj->tail + 1) % (obj->k + 1);//防止越界
return true;
}
}
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
{
return false;
}
obj->head = (obj->head + 1) % (obj->k + 1);//防止head越界
return true;
}
int myCircularQueueFront(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))//为空取不到队头的数据
{
return -1;
}
else
{
return obj->a[obj->head];
}
}
int myCircularQueueRear(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))//为空取不到队尾的数据
{
return -1;
}
else
{
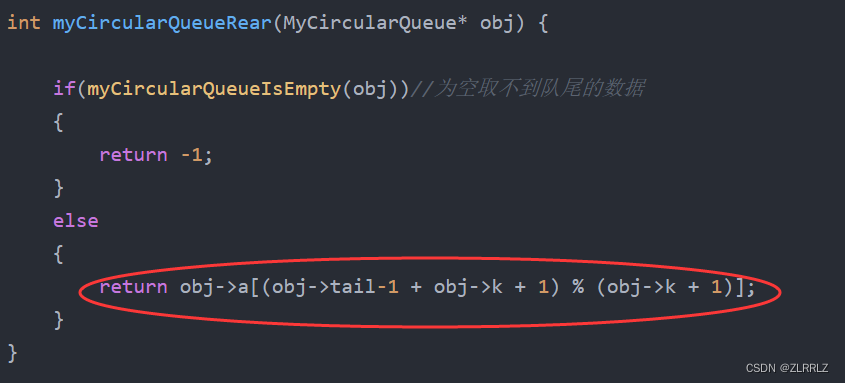
return obj->a[(obj->tail-1 + obj->k + 1) % (obj->k + 1)];
}
}
void myCircularQueueFree(MyCircularQueue* obj) {
free(obj->a);
free(obj);
}
/**
* Your MyCircularQueue struct will be instantiated and called as such:
* MyCircularQueue* obj = myCircularQueueCreate(k);
* bool param_1 = myCircularQueueEnQueue(obj, value);
* bool param_2 = myCircularQueueDeQueue(obj);
* int param_3 = myCircularQueueFront(obj);
* int param_4 = myCircularQueueRear(obj);
* bool param_5 = myCircularQueueIsEmpty(obj);
* bool param_6 = myCircularQueueIsFull(obj);
* myCircularQueueFree(obj);
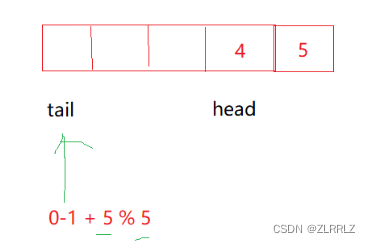
*/这里需要特别注意的是,当我们取队尾的数据时,由于tail是指向队尾数据的下一位,因此如果tail在数组头,tail-1取队尾就会出现负数的情况,因此与(tail+1)%(k+1)类似,我们要将(tail+1 +k+1)%(k+1),这样就可以避免出现,负数的情况,如果tail不在队头这样处理也不会有问题。
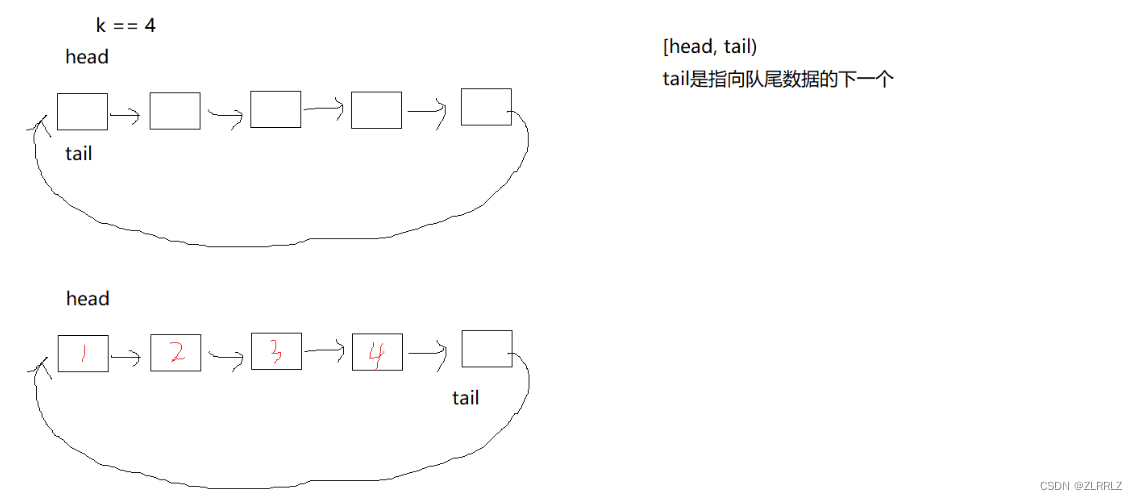
那么回到一开始的问题,为什么笔者说,使用链表不像看上去那样简单呢?首先,用链表形成循环队列,不像数组那样直接申请一块空间方便,其次由于tail是指向尾的下一个位置,因此我们如果想要找尾会很麻烦,对此可以使用双向链表、遍历寻找尾、专门创建变量记录tail前一个节点,总的来说,使用链表不光没有什么实质的好处,反而还会有不少麻烦。当然,如果读者想要用链表完成,也不无不可。
4.概念选择题
4.1题目
1.一个栈的初始状态为空。现将元素1、2、3、4、5、A、B、C、D、E依次入栈,然后再依次出栈,则元素出栈的顺序是( )。
A 12345ABCDE
B EDCBA54321
C ABCDE12345
D 54321EDCBA
2.若进栈序列为 1,2,3,4 ,进栈过程中可以出栈,则下列不可能的一个出栈序列是()
A 1,4,3,2
B 2,3,4,1
C 3,1,4,2
D 3,4,2,1
3.循环队列的存储空间为 Q(1:100) ,初始状态为 front=rear=100 。经过一系列正常的入队与退队操作 后, front=rear=99 ,则循环队列中的元素个数为( )
A 1
B 2
C 99
D 0或者100
4.以下( )不是队列的基本运算?
A 从队尾插入一个新元素
B 从队列中删除第i个元素
C 判断一个队列是否为空
D 读取队头元素的值
5.现有一循环队列,其队头指针为front,队尾指针为rear;循环队列长度为N。其队内有效长度为?(假设 队头不存放数据)
A (rear - front + N) % N + 1
B (rear - front + N) % N
C ear - front) % (N + 1)
D (rear - front + N) % (N - 1)
4.2答案
1.B //依次入栈,入完再出栈,后入先出
2.C //不可能出现2不出,就出到1
3.D //属于没有多开一个空间的方法,相等时可能为空,可能满。
4.B
5.B
5.附录源码:
5.1栈:
Stack.h
#pragma once
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
#include<stdio.h>
// 支持动态增长的栈
typedef int STDataType;
typedef struct Stack
{
STDataType* _a;
int _top; // 栈顶
int _capacity; // 容量
}Stack;
// 初始化栈
void StackInit(Stack* ps);
// 入栈
void StackPush(Stack* ps, STDataType data);
// 出栈
void StackPop(Stack* ps);
// 获取栈顶元素
STDataType StackTop(Stack* ps);
// 获取栈中有效元素个数
int StackSize(Stack* ps);
// 检测栈是否为空,如果为空返回0 ,如果不为空返回非零结果
bool StackEmpty(Stack* ps);
// 销毁栈
void StackDestroy(Stack* ps);
Stack.c
#include"Stack.h"
// 初始化栈
void StackInit(Stack* ps)
{
assert(ps);
ps->_a = NULL;
// top指向栈顶数据的下一个位置
ps->_top = 0;
// top指向栈顶数据
//ps->_top = -1;
ps->_capacity = 0;
}
// 入栈
void StackPush(Stack* ps, STDataType data)
{
assert(ps);
//扩容
if(ps->_capacity == ps->_top)
{
int newcapacity = ps->_capacity == 0 ? 4 : 2 * ps->_capacity;
STDataType* newnode = (STDataType*)realloc(ps->_a, newcapacity * sizeof(STDataType));
if (NULL == newnode)
{
perror("StackInit:realloc");
exit(1);
}
ps->_a = newnode;
ps->_capacity = newcapacity;
}
ps->_a[ps->_top] = data;
ps->_top++;
}
// 出栈
void StackPop(Stack* ps)
{
assert(ps);
assert(ps->_top > 0);
ps->_top--;
}
// 获取栈顶元素
STDataType StackTop(Stack* ps)
{
assert(ps);
assert(ps->_top > 0);
return ps->_a[ps->_top - 1];
}
// 获取栈中有效元素个数
int StackSize(Stack* ps)
{
assert(ps);
return ps->_top;
}
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
bool StackEmpty(Stack* ps)
{
assert(ps);
return ps->_top == 0;
}
// 销毁栈
void StackDestroy(Stack* ps)
{
assert(ps);
free(ps->_a);
ps->_a = NULL;
ps->_capacity = ps->_top = 0;
}
5.2队列
Queue.h
#pragma once
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include"stdbool.h"
typedef int QDataType;
// 链式结构:表示队列
typedef struct QListNode
{
struct QListNode* _next;
QDataType _data;
}QNode;
// 队列的结构
typedef struct Queue
{
QNode* _front;
QNode* _rear;
int _size;
}Queue;
// 初始化队列
void QueueInit(Queue* q);
// 队尾入队列
void QueuePush(Queue* q, QDataType data);
// 队头出队列
void QueuePop(Queue* q);
// 获取队列头部元素
QDataType QueueFront(Queue* q);
// 获取队列队尾元素
QDataType QueueBack(Queue* q);
// 获取队列中有效元素个数
int QueueSize(Queue* q);
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
bool QueueEmpty(Queue* q);
// 销毁队列
void QueueDestroy(Queue* q);
Queue.c
#include"queue.h"
// 初始化队列
void QueueInit(Queue* q)
{
q->_front = NULL;
q->_rear = NULL;
q->_size = 0;
}
// 队尾入队列
void QueuePush(Queue* q, QDataType data)
{
assert(q);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (NULL == newnode)
{
perror("QueuePush:malloc failed");
exit(1);
}
newnode->_data = data;
newnode->_next = NULL;
if (NULL == q->_rear)
{
q->_front = q->_rear = newnode;
}
else
{
q->_rear->_next = newnode;
q->_rear = newnode;
}
q->_size++;
}
// 队头出队列
void QueuePop(Queue* q)
{
assert(q);
assert(q->_size);
QNode* next = q->_front->_next;
free(q->_front);
q->_front = next;
if (q->_size == 1)
{
q->_rear = NULL;
}
q->_size--;
}
// 获取队列头部元素
QDataType QueueFront(Queue* q)
{
assert(q);
assert(q->_front);
return q->_front->_data;
}
// 获取队列队尾元素
QDataType QueueBack(Queue* q)
{
assert(q);
assert(q->_rear);
return q->_rear->_data;
}
// 获取队列中有效元素个数
int QueueSize(Queue* q)
{
assert(q);
return q->_size;
}
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
bool QueueEmpty(Queue* q)
{
assert(q);
return q->_size == 0;
}
// 销毁队列
void QueueDestroy(Queue* q)
{
assert(q);
QNode* cur = q->_front;
while(cur)
{
QNode* next = cur->_next;
free(cur);
cur = next;
}
q->_front = q->_rear = NULL;
q->_size = 0;
}
























 825
825

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










