简单程序语言理论与编译技术·7 Lambda演算

本文是记录专业课“程序语言理论与编译技术”的部分笔记。

LECTURE 7（Lambda演算）
1、Lambda演算早于计算机系统，把计算看做是函数的应用(application，一次替换)，允许无名函数进行函数抽象。是个很好的core language。
2、Lambda演算基础：

定义风格以lambda开头，后跟的n是参数，如上图的factorial函数。文法定义如下图：（要么是变量，要么是函数抽象，要么是代入）

上图最后一个例子，x是函数，y可能是值。
语法树、语义定义如下图：

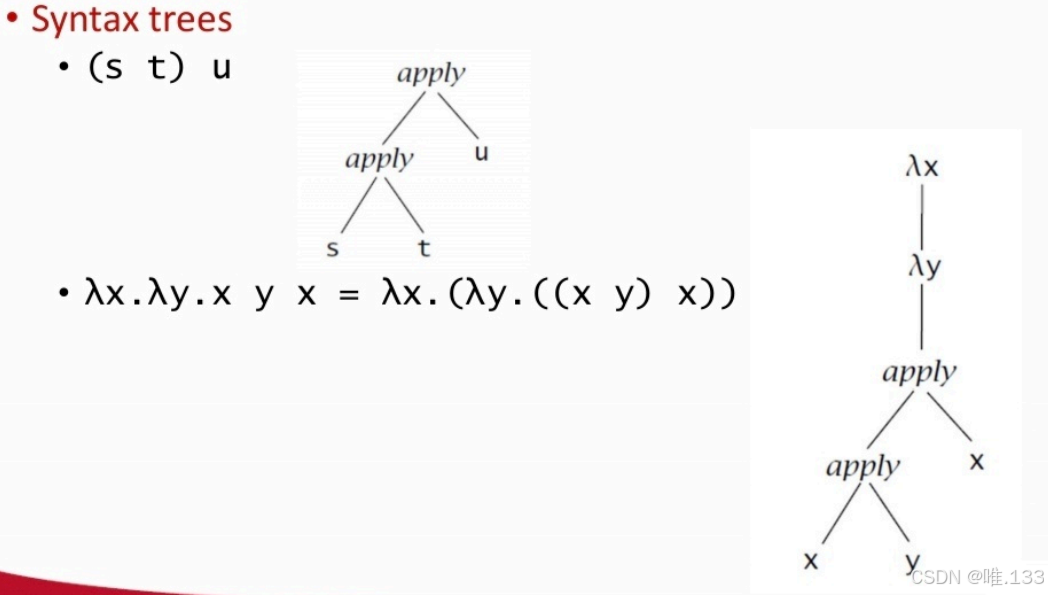
上图最后一个例子，内部未更换的那部分x是约束变量。语法树往上走没有lambda的就是自由变量，有的就是约束变量。替代时，蒙住第一个lambda，然后只替换自由变量（称为beta-reduction）

3、计算顺序很重要！以下是常见规定：

4、没有布尔型，可以添加定义函数如下图。这两个函数都有两个参数，tru只返回第一个参数，而tru和fls符合布尔计算，下例的test就可以看做if l then m else n。

tru tru fls是tru (tru fls)，返回括号里的第一个参数，即tru。
5、没有数据结构，也必须定义函数。序偶pair如下图。b是结构中的参数，用于传入tru或fls进而选择返回的参数。

6、数字常量的定义如下：

常量也是函数，在这里s是后继。scc的意思是，z作为零元，进行n次后继构造，在这基础上再次后继，得到n的后继。times是乘法。
https://lambdacalc.io/ 用于测试
前驱比较麻烦，重新定义数字常量的集合，提前存好自己的前驱，然后返回第一个参数就是返回前驱了。

7、函数无名，如何实现递归呢？观察omega不动，因此可以使用不动点来构造递归函数。

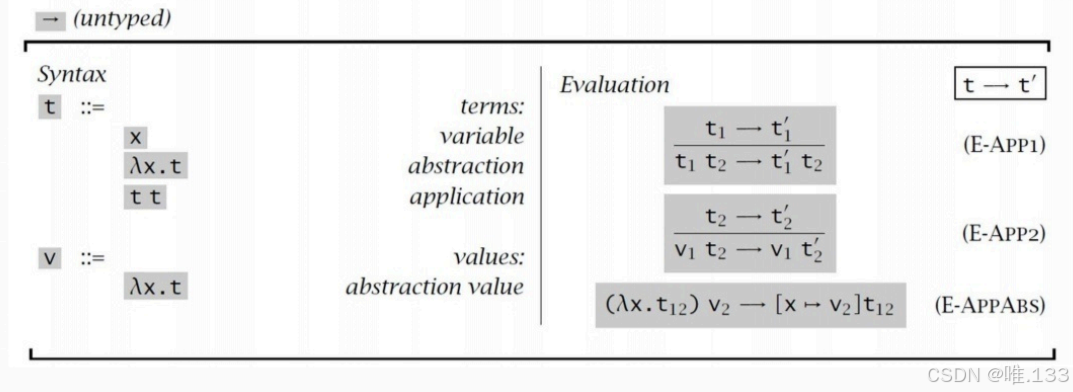
8、lambda演算的最终定义：