孩子们的游戏/约瑟夫环(链表模拟,数组模拟,队列模拟,动态规划四种解法)

题目

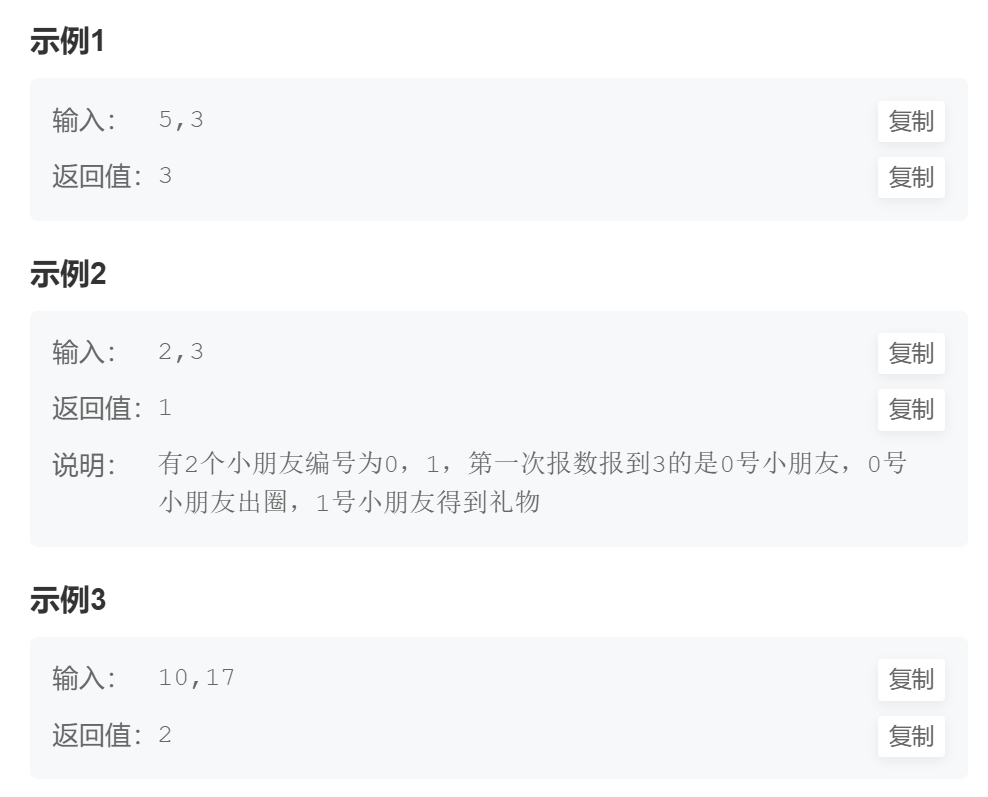
题目解析:

看完题目以后,你可能会嗅到一丝熟悉的味道,这不就是约瑟夫环换了一个说法吗.就是一群人围成一个环,然后进行报数游戏,报出数字的那个人出列,直到找到最后的赢家

算法原理

第一种:使用链表模拟

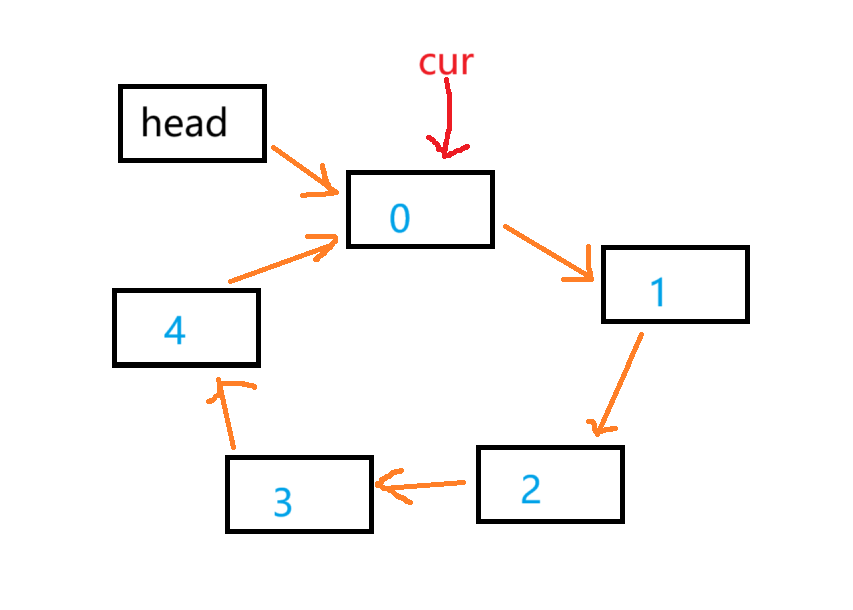
首先new出一个头结点标记起始位置,然后按照要求建立链表,然后一步一步的模拟过程,直到链表中只剩下一个元素.
注意:每次要删除一个节点的时候是会用到上一个节点的,因此需要prev指针保存cur的上一个节点信息

代码:

import java.util.*;
public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param n int整型 
     * @param m int整型 
     * @return int整型
     */
     static class Node{
        int val;
        Node next;
        public Node(int val,Node next){
            this.val = val;
            this.next = next;
        }
     }
      public int LastRemaining_Solution (int n, int m) {
        //构造链表:
        Node head = new Node(-1,null);
        Node cur = head;
        for(int i=0;i<n;i++){
            Node tmp = new Node(i,null);
            cur.next = tmp;
            cur = cur.next;
        }
        //成环:
        cur.next = head.next;

        //模拟整个过程:
        //注意一定要理清这个cur到底是从哪开始的,走几步停
        Node prev = head;
        cur = head.next;
        for(int i =0;i<n-1;i++){
            for(int j =1;j<=m-1;j++){
                prev = cur;
                cur = cur.next;
            }
            //此时的cur指向的就是要删除的元素
            prev.next = cur.next;
            cur = cur.next;
        }
        //将这个n-1个节点都删掉后,剩下的那个节点,prev和cur指针一定同时指向它
        int ret = cur.val;

        return ret;
        
    }
}

第二种:使用数组模拟

如果很陌生,强烈建议自己动手实践,切记脑子会了,手不一定会.耐住性子,相信自己,一步一个脚印,时间会检验一切.

正确思路

思路:使用一个数组存储元素,一个数组标记该元素是否已经被访问过,按照题意模拟
注意:我这里的示意图有"步长"这样的概念,这是自创的一个词汇,帮助理解的,仅限于此题,此方法,此人.
“步长”:规定是从起始位置找到停止位置的有效长度

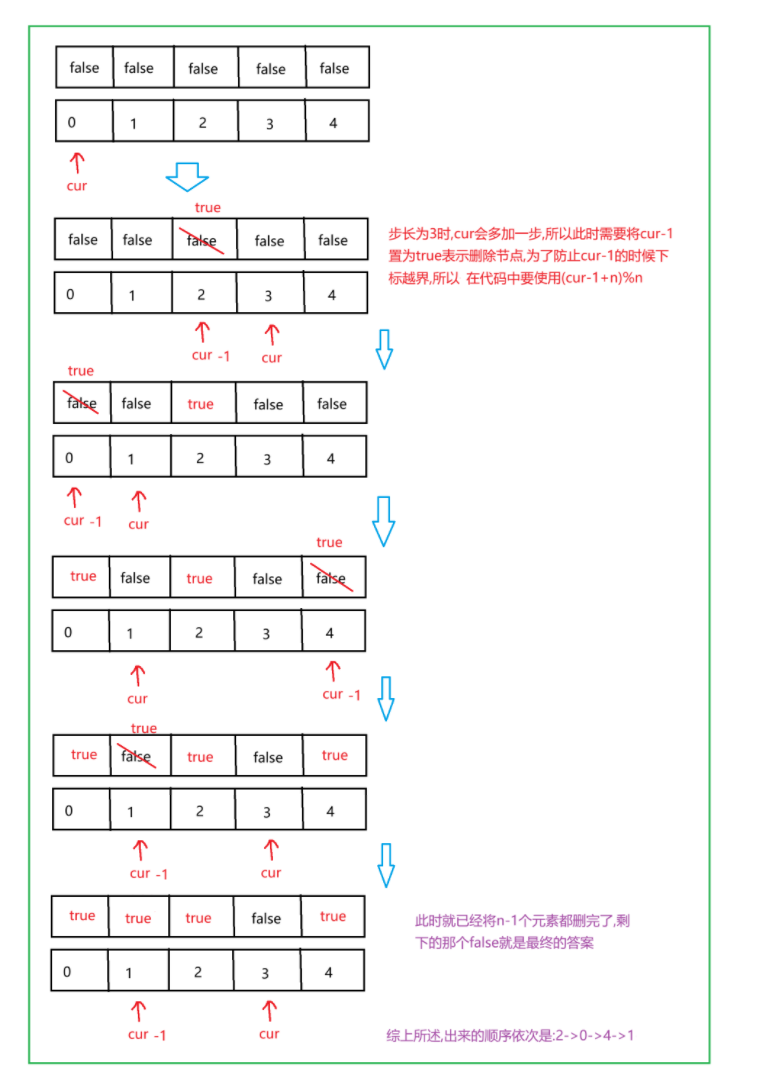
正确代码

 public static int LastRemaining_Solution (int n, int m) {
        int[] a = new int[n];
        //使用数组模拟:
        for(int i =0;i<n;i++)a[i] = i;
        //使用check数组来标记是否已经被删除掉了
        boolean[] check = new boolean[n];

        int cur = 0;
        for(int i =0;i<n-1;i++){
            int cnt = m;
            //这个while循环起到:找到下一个起始位置,以及遍历的作用
            while(cnt !=0){
                if(check[cur] == false){
                    cnt--;
                }
                cur=(cur+1)%n;
            }
            check[(cur-1+n)%n] = true;
            //原则上来讲,下一步需要找到cur的起始位置,但是由于while循环里使用了check[cur] == false进行判断
            //巧妙的节省了这一步
        }
        for(int i =0;i<n;i++){
            if(check[i]== false){
                return i;
            }
        }
        return -1;

    }

错误思路

“步长”,就是从起始位置找到停止位置的有效长度,这里设置成了cnt = m -1,
之所以这样搞,是主观上我们会更倾向于让 cur直接能指向要删掉的元素,而不是它的下一个,让我们看看是否有错.
思路虽然听起来好像很对,但是它有一个致命的错误:就是它将"步长"减了1,看起来好像没啥问题,但是:实际上cur指向的元素根本没有判断,那万一cur指向的元素已经被用过了呢?此时答案就错了,如下简图:

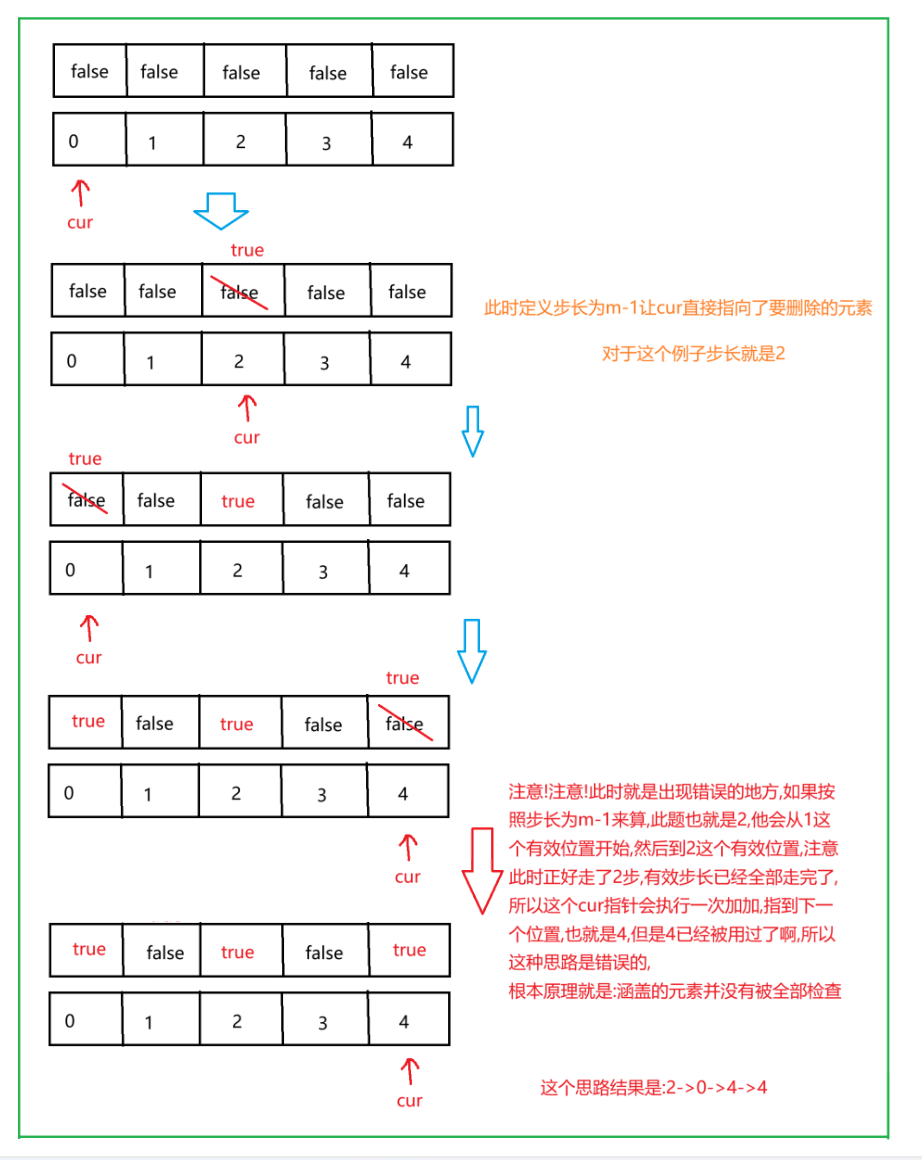
错误代码

 public static int LastRemaining_Solution2 (int n, int m) {
        int[] a = new int[n];
        for(int i =0;i<n;i++)a[i] = i;
        boolean[] check = new boolean[n];
        int cur = 0;
        for(int i =0;i<n-1;i++){
            int cnt = m-1;
            while(cnt !=0){
                if(check[cur] == false){
                    cnt--;
                }
                cur=(cur+1)%n;
            }
            check[cur] = true;
        }
        for(int i =0;i<n;i++){
            if(check[i]== false){
                return i;
            }
        }
        return -1;
    }

第三种:使用队列模拟

思路很简单:先将所有的元素都入队,模拟整个过程,要出队n-1个元素,每次将第m个元素给删掉,直到只剩下一个元素,即为答案

代码

 public int LastRemaining_Solution (int n, int m) {
        Queue<Integer> q = new LinkedList<>();
        //先将所有元素加入队列
        for(int i=0;i<n;i++)q.offer(i);
        n--;
        //将n-1个元素出队,剩下的那个就是答案
        while(n--!=0){
            int cnt = m -1; 
            while(cnt--!=0){
                q.offer(q.poll());
            }
            //删除元素:
            q.poll();
        }
        return q.peek();
    }

第四种:使用递推,动态规划思想

先看思路简图:

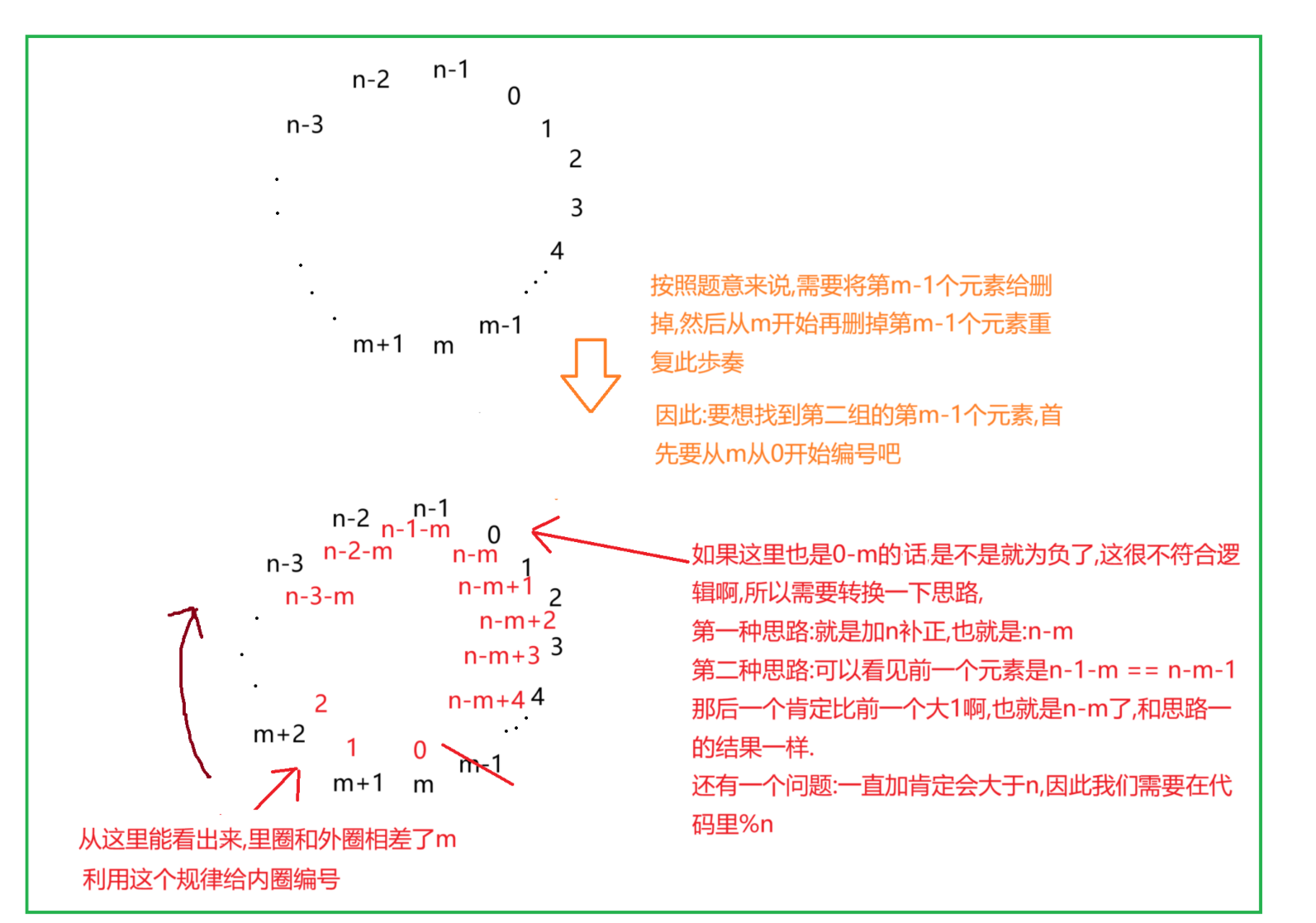
那这里的动态规划我们该怎么定义状态表示呢?怎么下手呢?
要知道,动态规划和递推是脱不了干系的,因为动态规划本质上使用的就是递推,所以这里和递推脱不了干系,根据以往的经验,都是根据前一个的状态推导后一个的状态,以上简图就是在找前一个轮的获胜这个和后一轮的获胜者的关系.
无论有多少个孩子在玩游戏,4个->3个->2个,他的获胜者是不是都是一样的,赢家没有变,只有编号变了.只需要找到编号变化的规律.

• 状态表示:所以dp[i]表示:当有i个孩子玩游戏时最终的获胜者的编号
• 转移方程:通过上诉简图不难发现,他们具有一一对应关系:

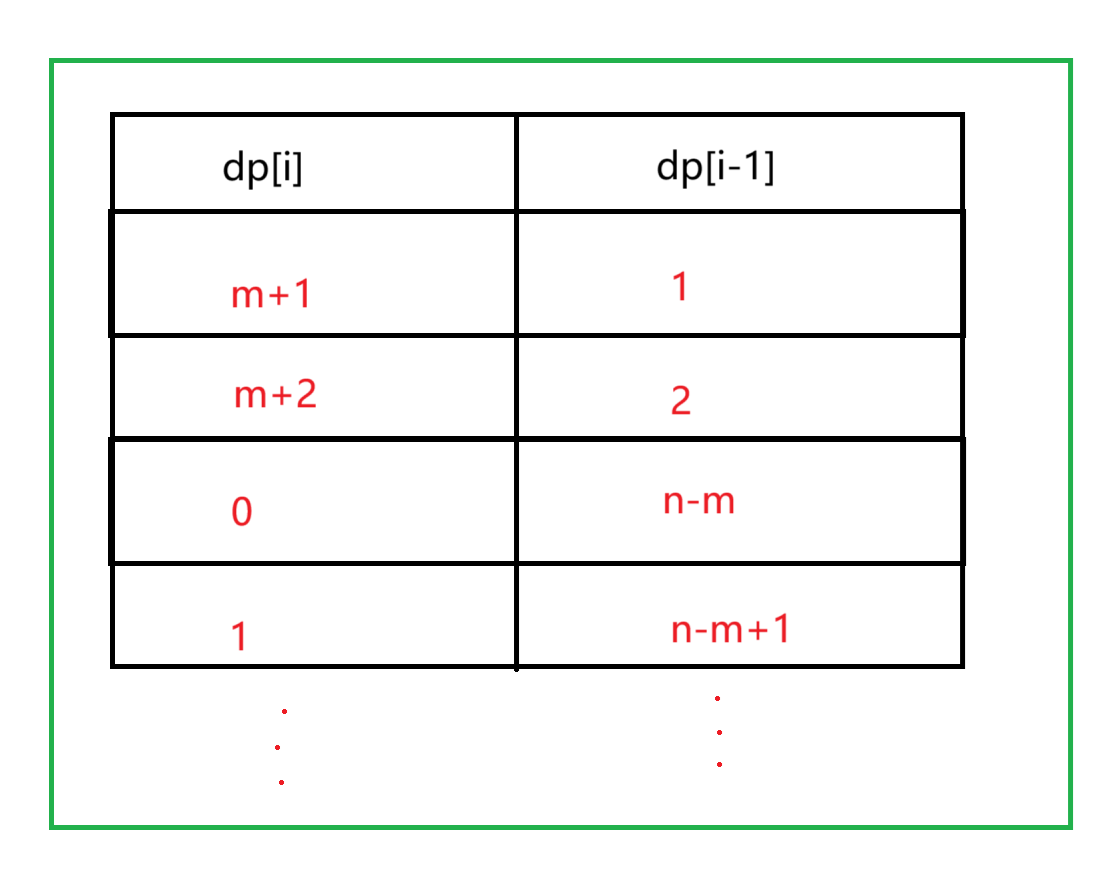
		dp[i] = (dp[i-1] +m)  %i

• 初始化:初始化dp[0] = 0,就能保证dp[1]正确
• 填表顺序:左->右
• 返回值:dp[n]

代码

当你深究这个dp过程的时候,你可能会疑惑,假设,n = 5,m = 3,
此时,算出来的具体过程就是:

• dp[1] = (dp[0]+3)%1 = 0
• dp[2] = (dp[1]+3)%2 = 1
• dp[3] = (dp[2]+3)%3 = 1
• dp[4] = (dp[3]+3)%4 = 0
• dp[5] = (dp[4]+3)%5 = 3
  不知道你会不会疑问,这里的结果除了dp[5]最终结果和我们手动使用链表/数组/队列推出来的结果对上了,其他的完全对不上.如果你在疑惑这,说明你已经成功的混了,这里的递推和之前的递推是完全不一样的两个东西,以前是按照歩奏一步一步模拟出来的,是按照固定的5个人做游戏一步一步模拟的.
  而此时是另一个思路,是按照有几个人做游戏来进行的,这里的人数是变化的,它涵盖了上诉的模拟,直接出了结果,可以说是一个全能的方法.

普通版:

      public int LastRemaining_Solution (int n, int m) {
        int[] dp = new int[n+1];
        for(int i=1;i<=n;i++){
            dp[i] = (dp[i-1] +m)%i;
        }
        return dp[n];
    }

进阶版:

有两种版本,第一种就是直接创建dp表的形式,但是还能简化

      public int LastRemaining_Solution (int n, int m) {
        int f =0;
        for(int i =1;i<=n;i++){
            f=(f+m)%i;
        }
        return f;
    }