二分查找（深入理解二分查找，每日一题）_为什么二分查找需要两个while循环,一个不能找到结果吗-优快云博客

本文详细解析了二分查找中的细节，包括正确设置while循环条件（left<=right），以及在特定情况下right的赋值。重点讲解了左右边界条件的区别，强调了在处理有序无重复数据时的正确实践。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

关于二分查找，我相信有很多人都已经会了，但是其中的一些细节，你可能没注意到
在这里插入图片描述
上面是力扣上的一道非常简单的基础题，但是，很多人可能虽然表面上学好了二分查找，但是，实际上，也是有一点小小的疑惑的，不过没有关系，跟进我的步伐，你一定会对他有一个更深刻的理解：在进入正文之前我们可以先熟悉一下二分查找的具体实现：代码如下：

class Solution {
    public int search(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;
        while(left <= right){//在这里我们的条件是<= 说明即使是left==rigt了也能进入循环，我们再下面会详细讲到
            int  mid = left + (right - left)/2;//这一步，很巧妙，既能达到（right+left）/2的效果，也能防止数字太大出现栈溢出的情况
            if(target < nums[mid]){//其实，这一步也是很多人的疑惑点，就是你可能想把这里的< 改成<= ，你认为假如等于了也没啥影响，
                //直接再判断一次，再返回不就行了；但是我想告诉你：你图啥呢？你与其在这个if语句里面判断一次到底是小于还是等于，还不如直接
                //从开始就分成三种情况呢，况且，从一开始分就只是需要三种情况，而你要是这样再分两种，就是2*2=4 种情况，你图啥呢？是吧
                //不过我相信你在看完我这个解析的时候机会恍然大悟，然后做出一些改变。
                right = mid-1;//这一步需要注意
            }
            else if(target > nums[mid]){
                left = mid + 1;//这一步也需要注意
            }
            else{
                return mid;

            }
        }
        return -1;

    }//以上代码这里力扣上运行也是没有问题的
    }

正文

对于二分查找，他的一个核心思想就是找出中间值然后进一步进行折半查找，反复循环，他的时间复杂度是O（logn），空间复杂度是：O（1）他的核心前提是我们查找的数据是有序的，并且没有重复（没有重复是因为：假如数据重复了，我们返回的下标可能就不唯一了，这样的结果就不准确了），在第一次写二分查找的时候我们可能会有这样一个疑问：到底我们的while 循环里的条件是left < right 还是left <= right 呢？正解：其实都是可以的
那么我们接下来就分两种情况对这个条件进行讨论（上面的代码是一种正解，在力扣上运行也是没有问题的）：

第一种：left <= right
对于这种情况，我们先不说结论，先进一步探究：我们依据上面的代码进行探究，
我们先探究第一个问题：这个left到底是应该等于 mid-1 还是mid呢？可能你猛然想一下好像都行，但是，这其实是不同的，我们就依据一个最简单的例子来说

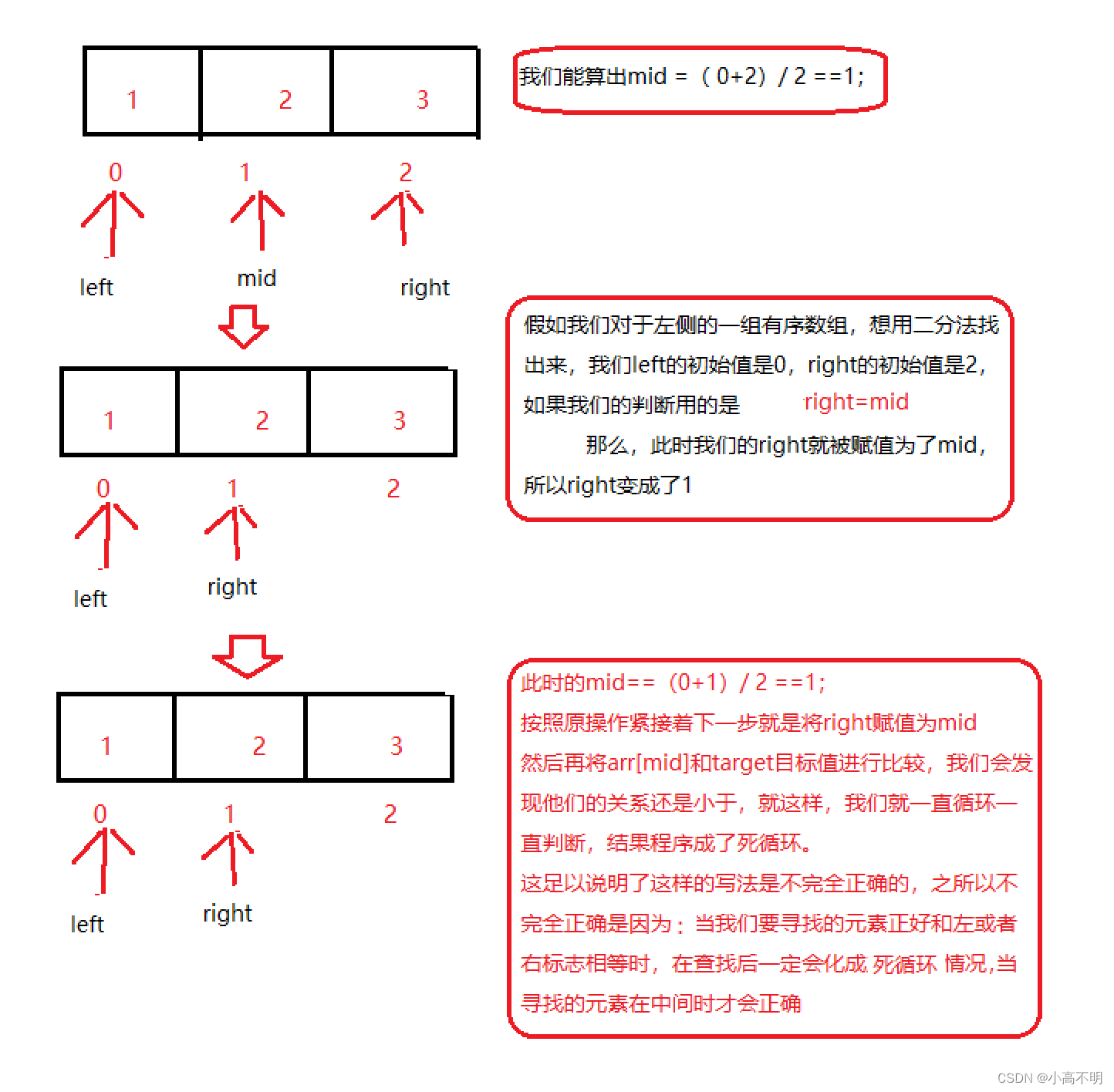
通过上面的简单的解答，我们也初步了解了right = mid 到底错在哪里了，接下来就有一个很明显的结论了：就是right=mid不对，那只有 right=mid-1对了。如果你这样想，那就又错了，为什么呢？你可能会问：不是只有两种情况吗？一个错，那另一个一定是对的，其实不是，这也是要分情况的，其实啊right=mid在某种情况下是对的，我们先上代码：

public int search(int[] nums, int target) {
        int left = 0;
        int right = nums.length ;//最大的秘密在这里，这是一个大前提，记住：好好体会这一步
        while (left < right){//这里和我们讨论的情况有些不一样，其实这也是我们将要引出的第二种判断方法的写法，这是要特别注意，只有在上面right=leng时候才能用
            int mid = left + (right - left)/2;
            if(target < nums[mid]){
                right = mid ;//你看他这不就来了， 这说明直接写right = mid也是正确的，只是我们要注意当有大前提的时候才能用，这一步要自己好好举例体会
            } else if (target > nums[mid]) {
                left = mid+1;//这一步就比较平常了
            }else{
                return mid;
            }
        }
        return -1;
    }
    //以上代码在力扣上运行也没有问题

上面与第一个代码最大的不同就是我们，将right直接赋值为了nums.length，这直接是数组的长度，如果用这个下标访问数组的话肯定是会发生越界访问的，所以毫无疑问，我们是默认将区间定义成了左闭右开，（在这里谈到区间你可能会有点懵，不过没关系，他的实质其实就是：原先的right不是增加了1吗，这时我们的赋值也要增加1，也就是mid-1+1），其实啊，上面的代码只有多多自己去悟才能深刻理解。
下面，我们就要说一下 left < right 和 left <=right 究竟有什么区别，我们以其他的所有歩奏都正确的前提下去思考这个问题，假如我们选择了第一种，我们知道如果target在 left 和 right 之间那肯定是能成功返回的，我们就考虑，target 正好与left或者right重合时的情况，这时，代码肯定会进行到我们上面的画图所展示的情况，只不过这次不是死循环了，left 可以和 right 重合了。但是，我们回头想一想，假如，我们把条件设置为left < right 那么当我们进行到最后一步的时候，我们会发现left一定会等于right，此时我们再进行一步循环就能得到结果，但是大前提left < right ，他不让我们进啊，所以啊，我们在最后需要手动 return mid；但是，你们们可以再动动你的小脑袋瓜，这样写是可以，但是我们写代码，求的不就是一次到底吗，有了更优的方案，我们绝对不会去取选择更差的方案，所以我呢还是最好选择正解。所以我们还是最好用left <= right ，上面的那种left < right 的情况是一种特例，只有在那种条件下才能用，要记住。
当然啊，看了这么多正面例子我们来看看反面的：

public int search2(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;
        while (left < right){//这里的写法也不全对，要时刻注意使用这一种用法的前提是int right= nums.length ；
            int mid = left + (right - left)/2;
            if(target < nums[mid]){
                right = mid ;//说明如下：
            } else if (target > nums[mid]) {
                left = mid;//这里和上面写的一致就足以确定一定在某些值上会发生死循环，这样的写法是不对的所以他在力扣上一定通不过
            }else{
                return mid;
            }
        }
        return -1;
    }