【回归预测】多元岭回归 (Ridge Regression) -MATLAB

 一、前言

        随着数据科学和机器学习的迅猛发展，回归分析作为一种经典的统计学方法，广泛应用于经济学、金融学、工程学等领域。在回归问题中，最小二乘法是一种常用的优化方法。然而，当面对多重共线性问题时，普通的线性回归方法可能会表现不佳。为了解决这一问题，多元岭回归（Ridge Regression）应运而生，它通过在损失函数中加入L2正则化项，有效避免了多重共线性和过拟合问题。

        本文将通过一个多元岭回归的实现示例，详细介绍多元岭回归的原理、相关公式及其应用，并逐步解析MATLAB代码的每个部分。通过实验，我们将展示如何使用多元岭回归进行模型训练、预测和性能评估。

---

二、技术与原理简介

        多元岭回归（Ridge Regression）是一种在线性回归的基础上，加入L2正则化项的回归模型。该方法通过惩罚回归系数的大小，减少模型的复杂度，从而提高其泛化能力。特别适用于自变量之间存在多重共线性（即自变量之间存在线性关系）的情况。

        1. 岭回归的基本思想

        岭回归的目标是通过最小化带有正则化项的损失函数来拟合模型。在普通最小二乘回归中，目标是最小化残差平方和：

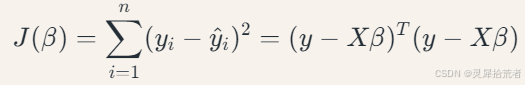
其中，𝑦 为目标变量，𝑋 为自变量矩阵，𝛽 为回归系数，𝑦^𝑖​ 为预测值。

        在岭回归中，目标函数增加了一个正则化项，用来惩罚回归系数的大小：

其中，𝜆 是正则化参数，𝜆≥0。当𝜆=0时，岭回归退化为普通的最小二乘回归；当𝜆很大时，回归系数趋近于零，模型更加简单。

        2. 岭回归的公式推导

        为求解最优回归系数，我们对目标函数 𝐽(𝛽) 进行最小化，得到以下推导结果：

        目标函数：

        对 𝛽 求导并令其为零：