【算法＋城堡问题、迷宫问题】BFS（广度优先）和DFS（深度优先）

目录

BFS（广度优先）算法

 DFS（深度优先）算法

城堡问题（DFS）

迷宫问题

BFS解法

DFS解法

BFS（广度优先）算法

BFS的代码实现可以描述为“BFS = 队列”，核心思想是从起始顶点开始，逐层访问所有相邻顶点。队列内的节点有以下两个特征：

（1）处理完第 i 层后，才会处理第 i + 1层

（2）队列中在任意时刻最多有两层节点，其中第 i 层节点都在第 i + 1 层前面 

例如以下图：先从顶点0开始广度优先遍历，首先访问顶点0

之后访问它的所有邻居顶点（距离顶点0的路径为1的顶点），该图中为1、2（1和2的顺序可以交换） 

接着访问距离为2的顶点，该图为3、4

以此类推 ，一直持续到将图中所有顶点访问完毕为止

下面详细介绍搜索相邻顶点的方法

 首先在邻接表中找到图对应的出边（例如0的相邻节点是1、2，则在矩阵中对应的是第0行中值为1、2的值标为1）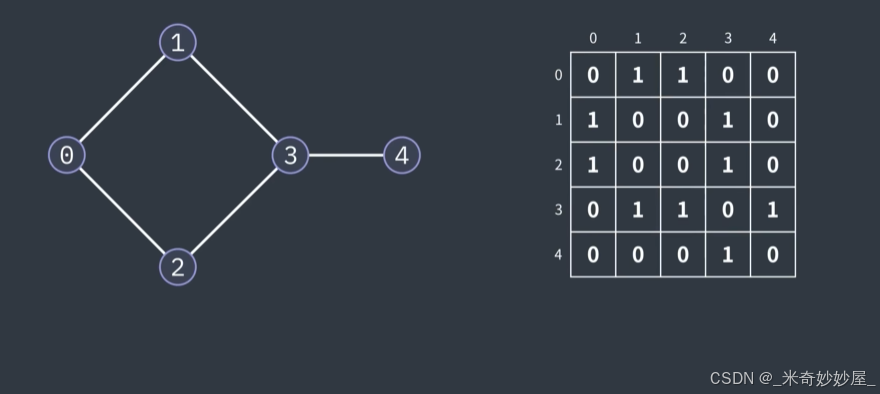

再在邻接表中找到顶点0对应的链表，从表头开始遍历

对于代码实现：首先声明一个访问标记数组（对应上图的链表），初始化为false，表示未访问过 

首先访问节点0，将数组0对应的位置改为true，表示已经访问过，再将顶点0进行入队操作，再判断队列是否为空（当前有顶点0不为空），将队列的对头元素0进行出队

通过矩阵，遍历顶点0所在行的元素，找到邻接顶点1、2 。判断顶点1是否被访问，如未访问过，就见标记数组中顶点1对应的值改为true，将顶点1入队，再判断顶点2是否被访问，重复上述操作，将2入队 。队列不为空，将对头元素1进行出队 

 再通过矩阵找到顶点1的邻接顶点0、3，顶点0的访问标记数组为true，说明被访问则不再重复访问，继续判断3是否被访问过，未访问就将标记数组的值改为true，将3入队，队列不为空则将队头元素2出队