【算法学习】尺取法（双指针）详解

_米奇妙妙屋_

已于 2024-12-11 22:25:13 修改

阅读量1.6k

点赞数 52

文章标签：算法学习 c++

于 2024-12-11 21:55:59 首次发布

本文链接：https://blog.youkuaiyun.com/2302_82116250/article/details/144315820

版权

前言

尺取法（又称双指针、Tow Pointers）常用来解决序列的区间问题。

一、二分法的介绍

应用背景：

1、给定一个序列，有时候需要它是有序的，进行排序

2、问题和序列的区间有关，且需要操作两个变量，可以用两个下标（指针）i 和 j 扫描区间

二分法优化原理：

把二重循环变成一重循环，在这个循环中同时处理 i 和 j ，复杂度也就从O(n^2)变成O(n)

二、用法介绍

1.反向扫描（对撞指针）

i、j 方向相反，i从头到尾，j从尾到头，在中间相会

终⽌条件⼀般是两个指针相遇或者错开（也可能在循环内部找到结果直接跳出循环），也就是：

left == right （两个指针指向同⼀个位置）

left > right （两个指针错开）

以下是具体应用：

找指定和的指数队

问题描述：

输入n（n<=100000）个整数，放在数组a[ ]中。找出其中的两个数，它们之间和等于整数m（假的肯定有解）。所有整数都是int型

假设m=5, 将数组排序（sort），再使用两个指针 i 和 j，分别从数组的开始和结束位置向中间遍历

计算 sum = a[i] + a[j] = 1 + 9 = 10，因为 6 > 5，说明加的数太大，需要减小被加数，所以 j--

不断重复以上判断直到sum = a[i] + a[j] = 1 + 4 = 5，因为 5 == 5，输出 1 4，然后 i++ 和 j--

代码实现

void find_sum(int a[ ], int n, int m){
    sort(a,a+n);
    int i = 0, j = n - 1;
    while(i < j){
        int sum = a[i] + a[j];
        if(sum > m)
            j--;
        if(sum < m)
            i++;
        if(sum == m){
            cout << a[i] << " " << a[i] << endl;
            i++;
            j--;
        }
    }
}

2.同向扫描（快慢指针）

i、j方向相同，从头到尾，可以让 j 跑在 i 前面

使用两个移动速度不同的指针在数组或链表等序列结构上移动。这种方法对于处理环形链表或数组非常有用。

其实不单单是环形链表或者是数组，如果我们要研究的问题出现循环往复的情况时，均可考虑使用快慢指针的思想

寻找区间和

问题描述：

给定一个长度为 n 的数组 a[ ] 和一个数 s ，在这个数组中找一个区间，使这个区间的数组元素之和等于 s 。输出区间的起点和终点位置

思路：

如果sum = s，输出一个解，继续，把sum减掉元素a[ i ]，并把 i 向后移动一位

如果sum > s，让sum减掉元素 a[ i ]，并把 i 向后移动一位

如果sum < s，把 j 向后移动一位，并把sum的值加上这个新元素

假设给定的 s = 6，初始 i = 0，j = 0（都指向第1个元素） sum = a [ 0 ] = 1

sum < s，所以 j++，sum += a[j] = 1 + 2 = 3

i = 0, j = 1, sum = 3

sum < s，所以 j++，sum += a[j] = 3 + 3 = 6

sum == s，输出 0 2

sum -= a[i] = 6 - 1 = 5，i++

i = 1, j = 2, sum = 4

sum < s，所以 j++，sum += a[j] = 5 + 7 = 12

sum > s，所以 sum -= a[i] = 12 - 7 = 5，i++

不断重复以上遍历

此时i > j ，sum -= a[j] = 13 - 7 = 6，j++

重复以上操作直至遍历完数组中的所有元素

void findsum(int *a, int n, int s) {
    int i = 0, j = 0;
    int sum = a[0];
    while (j < n) {
        if (sum >= s) {
            if (sum == s) {
                cout << i << " " << j << endl; 
            }
            sum -= a[i]; 
            i++; 
            if (i > j) {
                j++;
                if (j < n) sum += a[j];
            }
        } 
        else {
            j++;
            if (j < n) sum += a[j];
        }
    }
}

3、多指针

有时候两个指针不够用，需要更多指针

总体思路：

定义三个指针k，i，j，先固定 k 的位置不变，通过移动 i ，j 的位置寻找当 k 一定时符合提议的答案，在移动 k 的位置，同时改变 i , j 的检索范围，直至 k ，i , j ,指向最后三个元素的位置

初始状态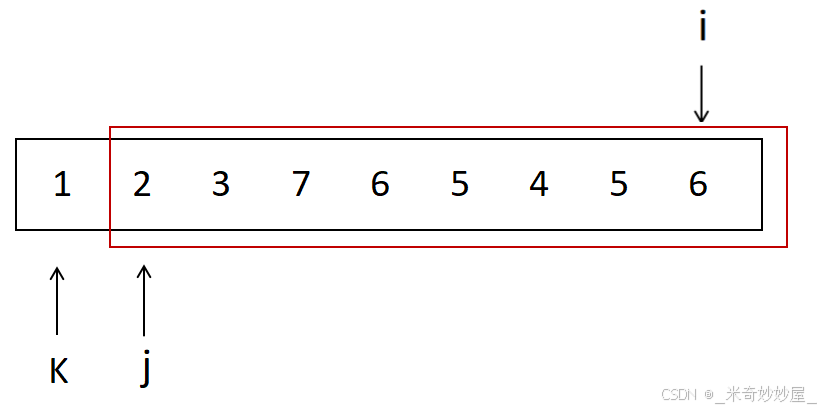

检索完毕，移动 k 的位置，缩小 i , j 的检索范围

不断重复，直至到达结束位置（假设有序列nums，结束条件为：k < nums.size() - 2）

问题描述：

给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c 使得 a + b + c = 0 ？请你找出所有和为 0 且不重复的三元组。

注意： 答案中不可以包含重复的三元组

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

vector<vector<int>> threeSum(vector<int>& nums) {
    vector<vector<int>> result;
    if (nums.size() < 3) return result;
    
    sort(nums.begin(), nums.end());
    int n = nums.size();
    
    for (int i = 0; i < n - 2; ++i) {
        if (i > 0 && nums[i] == nums[i - 1]) continue; // 跳过重复元素
        
        int j = i + 1, k = n - 1;
        while (j < k) {
            int curSum = nums[i] + nums[j] + nums[k];
            if (curSum == 0) {
                result.push_back({nums[i], nums[j], nums[k]});
                ++j;
                --k;
                while (j < k && nums[j] == nums[j - 1]) ++j; // 跳过重复元素
                while (j < k && nums[k] == nums[k + 1]) --k; // 跳过重复元素
            } else if (curSum < 0) {
                ++j;
            } else {
                --k;
            }
        }
    }
    
    return result;
}