模糊聚类分析

Hole_up

于 2025-05-10 13:54:47 发布

阅读量963

点赞数 9

CC 4.0 BY-SA版权

分类专栏：数学建模 matlab 机器学习文章标签：人工智能算法机器学习数学建模模糊数学

本文链接：https://blog.youkuaiyun.com/2302_81240667/article/details/147784670

数学建模同时被 3 个专栏收录

15 篇文章

订阅专栏

matlab

6 篇文章

订阅专栏

机器学习

3 篇文章

订阅专栏

模糊集理论

简介

模糊集理论（Fuzzy Set Theory）是处理不确定性和模糊性现象的一种数学理论，由美国控制论专家扎德（Lotfi A. Zadeh）于1965年首次提出。这一理论突破了传统集合论中“非此即彼”的严格划分，为解决现实世界中大量存在的模糊性问题提供了有效工具。

提出者：扎德教授在1965年的论文中首次提出了模糊集的概念。
核心思想：模糊集理论认为，一个元素可以以不同的程度属于某个集合，而非传统集合论中的“属于”或“不属于”。

核心概念

（1）模糊集合

模糊集合是模糊集理论的核心概念。与普通集合不同，模糊集合允许元素以不同的隶属度（介于0和1之间）属于某个集合。例如，在“高个子”的模糊集合中，身高180cm的人可能隶属度为0.9，而身高170cm的人可能隶属度为0.5。

（2）隶属函数

隶属函数是模糊集合的数学表达方式，用于描述元素对集合的隶属程度。例如，对于“高个子”这一模糊集合，隶属函数可以定义为：

$\mu =x-\frac{x-20}{160}$

其中，x表示身高（单位：cm），μ(x)表示隶属度。当身高为180cm时，μ(180)=1，表示完全属于“高个子”集合；当身高为160cm时，μ(160)=0μ(160)=0，表示完全不属于该集合。

（3）模糊运算

模糊集合支持多种运算，包括并集、交集和补集等，这些运算基于隶属度函数进行计算。例如：

并集：两个模糊集合的并集的隶属度是两个集合隶属度的最大值。
交集：两个模糊集合的交集的隶属度是两个集合隶属度的最小值。
补集：模糊集合的补集的隶属度是1减去原隶属度。

模糊特征的事物

带有模糊特征的事物是指那些边界不清晰、难以用精确的数学语言来描述的事物。它们往往具有以下特点：

边界不清晰: 它们没有明确的界限，与其他事物的区分是渐进的，而不是突变的。例如，"高个子"和"矮个子"之间没有明确的界限，身高在170cm到180cm之间的人既可以被认为是高个子，也可以被认为是矮个子。
不确定性: 它们的属性或状态不是确定的，而是存在一定的概率或可能性。例如，明天的天气可能是晴天、阴天或雨天，我们无法完全确定，只能预测各种天气情况发生的概率。
主观性: 它们的分类或评价标准往往带有主观性，不同的人可能会有不同的看法。例如，对于"美丽的风景"的定义，每个人心中都有自己的标准。
复杂性: 它们往往涉及多个因素，这些因素之间相互影响，使得事物难以用简单的模型来描述。例如，股票市场的走势受到经济、政治、社会等多种因素的影响，难以准确预测。

FCM算法

模糊C-均值聚类算法（Fuzzy C-Means, FCM）是一种基于模糊集理论的经典聚类算法，广泛用于数据分析、图像处理等领域。

1. 算法概述

模糊C-均值聚类算法（FCM）是一种无监督学习算法，用于将数据点划分到不同的类别中，属于软聚类算法。与传统的硬聚类算法（如K-means）不同，FCM允许数据点以不同的隶属度同时属于多个类别，从而更好地处理数据中的模糊性和不确定性。

核心思想：通过计算每个数据点对所有聚类中心的隶属度，将数据点划分为多个类别，并不断优化隶属度和聚类中心，最终得到稳定的聚类结果。
提出背景：FCM算法由扎德教授提出，旨在解决传统聚类算法在处理模糊性数据时的局限性。

2. 原理与步骤

FCM算法的核心在于模糊隶属度和聚类中心的迭代更新。以下是算法的具体步骤：

（1）初始化

确定参数：选择聚类数量 K和模糊因子 m（通常 m取值为1.5到2.5之间）。
初始化隶属度矩阵：随机生成一个 N×K的隶属度矩阵 U，其中 N 是数据点的数量，K是聚类数量。矩阵中的每个元素 $u_{ij}$ 表示数据点 i 属于聚类 j 的隶属度，满足 0≤ $u_{ij}$ ≤1且每行元素之和为1。

（2）计算聚类中心

根据当前的隶属度矩阵 U 计算每个聚类的中心 Cj。
聚类中心 Cj 是数据点的加权平均值，权重由隶属度决定。计算公式为：

$C_{j}=\frac{\sum_{i=1}^{N}\cdot u_{ij}^{m}\cdot X_{i}}{\sum_{i=1}^{N} u_{ij}^{m}}$

其中，Xi是数据点 i 的位置， $u_{ij}$ 是数据点 i 属于聚类 j 的隶属度，m 是模糊因子。

（3）更新隶属度

根据当前的聚类中心Cj更新隶属度矩阵 U。
隶属度 uij的计算公式为：

$u_{ij}=\frac{1}{\sum_{k=1}^{K} (\frac{\left \| X_{i}-C_{j} \right \|}{\left \| X_{i}-C_{k} \right \|})}$

其中， $\left \| X_{i}-C_{j} \right \|$ 表示数据点 i 到聚类中心Cj的欧氏距离。

（4）迭代

重复步骤（2）和（3），直到隶属度矩阵 U和聚类中心 C的变化小于某个阈值，或者达到预设的迭代次数。

3. 优缺点

优点

灵活性：允许数据点以不同隶属度属于多个类别，适用于模糊性数据的处理。
鲁棒性：对噪声和异常值具有一定的抗干扰能力。
应用广泛：在图像处理、市场分析、生物信息学等领域表现优异。

缺点

参数敏感：聚类数量 K 和模糊因子 m 的选择对结果影响较大。
计算复杂度：迭代过程需要多次计算距离和隶属度，计算量较大。
主观性：隶属度矩阵的初始化和参数选择可能依赖于经验。

模糊聚类一般步骤

建立数据矩阵

在实际问题中，数据又不同的量纲，需要标准化。

标准差标准化

${x_{ij}^{'}}=\frac{x_{ij}-\overline{x_{j}}}{S_{j}}^{}$

其中， $\overline{x_{j}}$ 是平均数， $S_{j}$ 是标准差。

适用于数据呈正态分布的情况（钟形曲线）。通过将数据转换为均值为0，标准差为1的分布，可以消除量纲的影响，使不同量纲的数据可以进行比较。

极差正规化

${x_{ij}^{'}}=\frac{x_{ij}-min\{x_{ij}\}}{max\{x_{ij}\}-min\{x_{ij}\}}$

适用于数据不需要遵循正态分布的情况。通过将数据缩放到一个固定的范围（通常是0到1），可以保持数据的原始分布形状，同时消除量纲的影响。

极差标准化

${x_{ij}^{'}}=\frac{x_{ij}-\overline{x_{j}}}{max\{x_{ij}\}-min\{x_{ij}\}}$

与极差正规化类似，但处理方式略有不同，具体选择取决于数据的特点和分析需求。

最大值规格化

${x_{ij}^{'}}=\frac{x_{ij}}{M_{j}}$

其中， $M_{j}$ 为第j列中的最大数

适用于需要突出数据中最大值的情况。通过将数据除以最大值，可以消除量纲的影响，并使数据在0到1之间。

建立模糊相似矩阵

距离法

适用于分析变量之间的距离或差异。

贴近度法

最大最小法

$r_{ij}=\frac{\sum_{k=1}^{m}\left | x_{ik}\wedge x_{jk} \right |}{\sum_{k=1}^{m}\left | x_{ik}\vee x_{jk} \right |}$

适用于分析变量之间的相似度。通过计算变量之间的最大最小相似度，可以衡量它们之间的相似性。

算数平均法

$r_{ij}=\frac{\sum_{k=1}^{m}\left | x_{ik}\wedge x_{jk} \right |}{\frac{1}{2}\sum_{k=1}^{m}\left | x_{ik}+x_{jk} \right |}$

适用于分析变量之间的相似度。通过计算变量之间的算数平均相似度，可以衡量它们之间的相似性。

几何平均法

$r_{ij}=\frac{\sum_{k=1}^{m}\left | x_{ik}\wedge x_{jk} \right |}{\sum_{k=1}^{m}\sqrt{x_{ik}\cdot x_{jk}}}$

适用于分析变量之间的相似度。通过计算变量之间的几何平均相似度，可以衡量它们之间的相似性。

指数相似法

适用于分析变量之间的相似度。通过计算变量之间的指数相似度，可以衡量它们之间的相似性。

兰氏距离法

$r_{ij}=1-C\left [\sum_{k=1}^{m}\left | \frac{x_{ik}-x_{jk}}{x_{ik}+x_{jk}} \right | \right ]^a$

适用于分析变量之间的距离或差异。通过计算变量之间的兰氏距离，可以衡量它们之间的相似性。

绝对值指数法

适用于分析变量之间的相似度。通过计算变量之间的绝对值指数相似度，可以衡量它们之间的相似性。

绝对值导数法

适用于分析变量之间的相似度。通过计算变量之间的绝对值导数相似度，可以衡量它们之间的相似性。

模糊矩阵可以对论域进行划分，这正是聚类分析所需要的。

例题

考虑某环保部门对该地区的5个环境区域,按照污染情况进行分类,设每个区域包含空气、水分、土壤、作物四个要素,环境区域的污染情况由污染物在四个要素中的含量的超过程度来衡量.设这5个环境区域的污染程度数据为

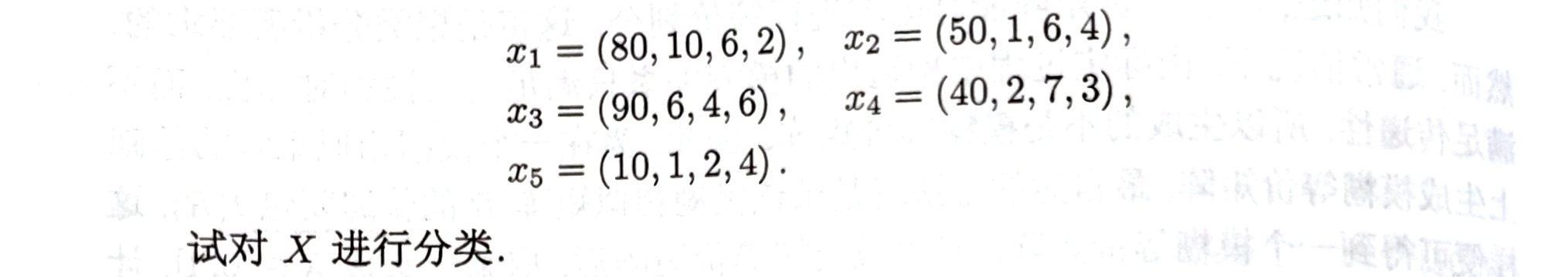
解题

数据标准化

选择最大值规格化法进行标准化的原因如下：

突出最大污染程度：最大值规格化法将每个要素的值除以该要素的最大值，这样可以将最大的污染程度标准化为1，而其他值则介于0和1之间。这种标准化方法可以突出每个要素中最大的污染程度，使得分析者能够直观地看出哪些区域或要素的污染最为严重。
保持相对差异：通过最大值规格化，虽然数值范围被压缩到了0到1之间，但各个区域或要素之间的相对差异得到了保留。这意味着，如果某个区域的空气污染程度是另一个区域的两倍，那么在标准化后，这种两倍的差异关系仍然存在。
简化计算：最大值规格化法的计算相对简单，只需要找到每个要素的最大值，然后进行除法运算。这种简化计算在实际应用中是非常有用的，特别是当处理大量数据时。
适用于比较分析：由于所有数据都被标准化到了0到1的范围，因此可以很容易地对不同区域或要素的污染程度进行直接比较。这种比较分析在环境评估中是非常重要的，因为它可以帮助决策者识别出需要优先关注的问题区域或要素。
符合问题背景：在这个特定的题目中，污染程度是由污染物在四个要素中的含量的超过程度来衡量的。使用最大值规格化法可以直观地展示出每个要素中污染物的超过程度相对于最大超过程度的比例，这符合问题的背景和需求。

模糊相似矩阵

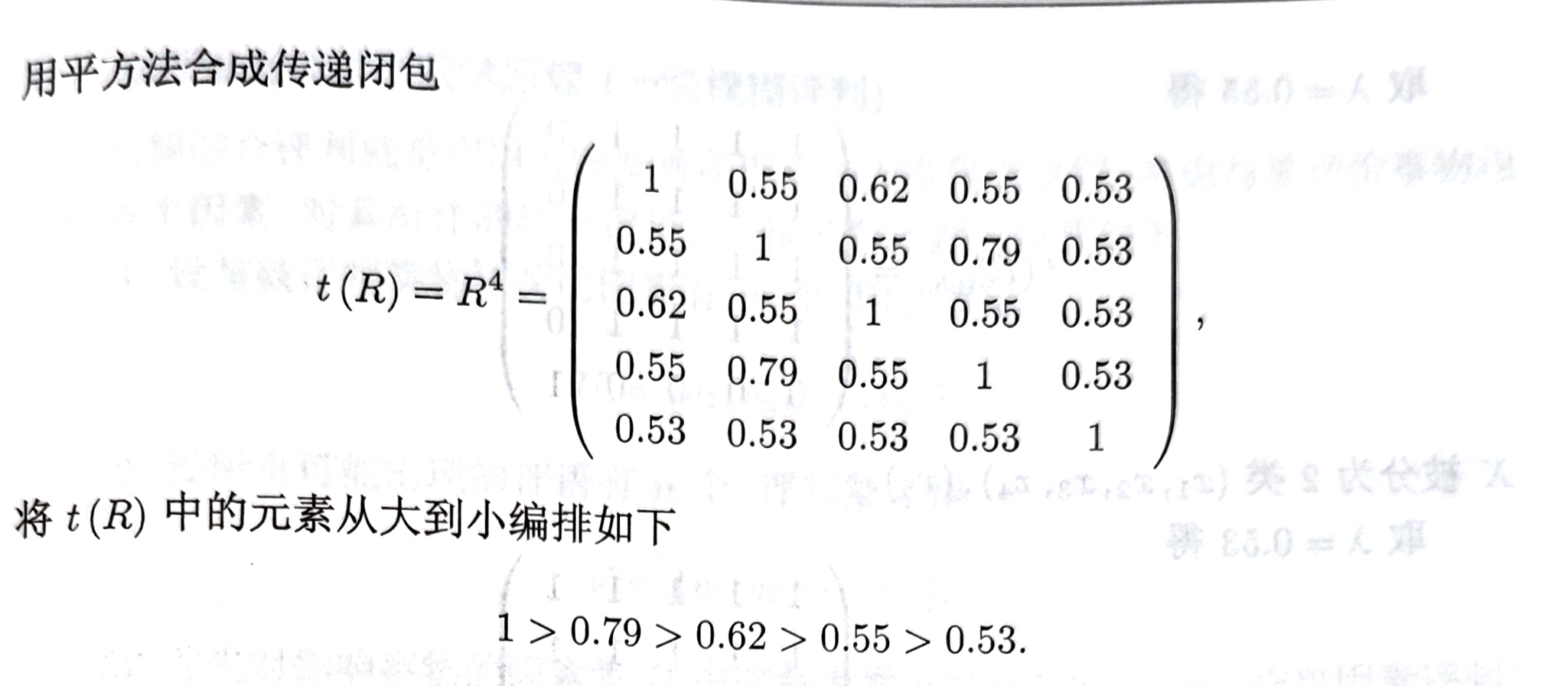
分类讨论

代码

编程题目：模糊 C 均值聚类算法实现与可视化

问题描述：
编写 MATLAB 代码实现模糊 C 均值聚类（Fuzzy C-Means, FCM）算法，并应用于二维数据集的聚类分析。

%% 参数设置与数据生成
rng(20250508); % 固定随机种子保证可复现
c = 2;         % 聚类类别数
m = 2;         % 模糊指数（通常取2）
n = 200;       % 总样本数（每类100个）
iter_max = 10; % 最大迭代次数

% 生成两类二维数据
mu1 = [2, 2];     Sigma1 = eye(2);     % 第一类参数
mu2 = [-2, -2];   Sigma2 = 2*eye(2);   % 第二类参数
X1 = mvnrnd(mu1, Sigma1, 100);         % 第一类数据（100×2）
X2 = mvnrnd(mu2, Sigma2, 100);         % 第二类数据（100×2）
X = [X1; X2];                          % 合并数据集（200×2）

%% 初始化隶属度矩阵（n×c，每行和为1）
U = rand(n, c);                        % 随机生成初始隶属度
U = U ./ repmat(sum(U,2), 1, c);       % 行归一化保证和为1

%% 模糊C均值迭代优化
for iter = 1:iter_max
    % 计算聚类中心（c×2矩阵）
    v = (U.^m)' * X ./ repmat(sum(U.^m,1)', 1, 2);  % 正确维度：(c×n)*(n×2) = c×2
    
    % 计算样本到各中心的欧氏距离（n×c矩阵）
    dist = pdist2(X, v);  % n×c矩阵（每行是样本到c个中心的距离）
    
    % 修正：隶属度更新公式的正确矩阵实现（关键修改）
    D = dist.^(2/(m-1));                % 距离的2/(m-1)次方（n×c）
    U_new = D ./ repmat(sum(D,2), 1, c); % 每行除以该行和（保证行和为1）
    U_new(isnan(U_new)) = 1/c;          % 处理距离全零的特殊情况（如所有中心重合）
    
    % 检查收敛（维度一致，现U_new与U均为n×c）
    if max(max(abs(U_new - U))) < 1e-5
        break;
    end
    U = U_new;
end

%% 可视化结果（代码保持不变）
figure('Position', [100 100 800 600])

% 绘制原始数据（用真实类别区分）
subplot(1,2,1)
scatter(X1(:,1), X1(:,2), 30, [0 0.5 1], 'filled')  % 第一类蓝色
hold on
scatter(X2(:,1), X2(:,2), 30, [1 0.3 0.3], 'filled') % 第二类红色
title('原始数据分布（真实类别）')
xlabel('X1'), ylabel('X2')
axis square tight

% 绘制聚类结果（用隶属度最大值分类）
subplot(1,2,2)
[~, label] = max(U, [], 2);        % 获取硬分类标签
color = [label==1, label==2] * [0 0.5 1; 1 0.3 0.3];  %颜色映射
scatter(X(:,1), X(:,2), 30, color, 'filled')
hold on
scatter(v(:,1), v(:,2), 200, [0 0 0], 's', 'LineWidth', 2)  %聚类中心（黑色方块）
title('模糊C均值聚类结果（迭代10次）')
xlabel('X1'), ylabel('X2')
axis square tight
legend('聚类中心', 'Location', 'best')

sgtitle('模糊C均值聚类（FCM）修正版 | 数据生成参数：均值[2,2]/[-2,-2]，协方差I/2I')