引言
在现实世界中,我们面临的问题往往充满了不确定性。无论是医疗诊断、金融分析还是智能控制,都需要人工智能系统能够处理不完整、不准确或模糊的信息。本章将深入探讨不确定性推理的核心方法,帮助读者理解如何让机器在不确定环境中做出合理决策。
本章知识思维导图

4.1 不确定性推理的概念
不确定性推理是指在证据和知识都不确定的情况下,通过运用不确定性知识进行的推理。不确定性主要来源于以下几个方面:
- 知识的不确定性:规则本身的正确性不确定
- 证据的不确定性:观察到的证据不完整或有误差
- 结论的不确定性:推理结果的不确定性
不确定性推理的基本问题
- 不确定性的表示:包括知识不确定性的表示和证据不确定性的表示
- 不确定性的匹配:判断证据与知识的匹配程度
- 组合证据不确定性的计算:多个证据组合时的不确定性计算
- 不确定性的传递:推理过程中不确定性的传递算法
- 结论不确定性的合成:多个推理路径得到结论的不确定性合成
不确定性推理的类型
常见的不确定性推理方法可分为如下几类:
- 模型方法:对不确定性的表示与处理建立明确的模型
- 数值方法:用数值表示不确定性,如概率方法、可信度方法等
- 非数值方法:如古典逻辑方法、非单调推理方法等
- 控制方法:通过控制策略来处理不确定性,如启发式搜索等
4.2 可信度方法
可信度方法是由 Shortliffe 等人在确定性理论的基础上,结合概率方法提出的一种不确定性推理方法,广泛应用于专家系统中。
基本概念
-
可信度:对某一命题的相信程度,用 CF (H,E) 表示,取值范围 [-1,1]
- CF (H,E)>0:证据 E 支持结论 H
- CF (H,E)=0:证据 E 与结论 H 无关
- CF (H,E)<0:证据 E 不支持结论 H
-
可信度的计算:
- 证据 E 的可信度 CF (E)
- 规则的可信度 CF (H,E)
- 结论 H 的可信度 CF (H) = CF (H,E) × max {0, CF (E)}
组合证据的可信度计算
- 合取证据:E = E1 ∧ E2 ∧ ... ∧ En,CF(E) = min{CF(E1), CF(E2), ..., CF(En)}
- 析取证据:E = E1 ∨ E2 ∨ ... ∨ En,CF(E) = max{CF(E1), CF(E2), ..., CF(En)}
可信度方法案例与代码实现
下面通过一个医疗诊断的例子来实现可信度方法:
import numpy as np
class CertaintyFactorSystem:
def __init__(self):
# 存储规则库:{结论: [(证据列表, 可信度)]}
self.rules = {
"感冒": [
(["头痛", "流鼻涕"], 0.7),
(["发热", "咳嗽"], 0.8)
],
"肺炎": [
(["发热", "咳嗽", "胸痛"], 0.9),
(["发热", "呼吸困难"], 0.85)
],
"过敏": [
(["流鼻涕", "打喷嚏", "皮肤瘙痒"], 0.8),
(["眼睛红肿", "流鼻涕"], 0.75)
]
}
# 存储证据的可信度
self.evidence_cf = {}
def set_evidence_cf(self, evidence, cf):
"""设置证据的可信度"""
self.evidence_cf[evidence] = cf
def get_evidence_cf(self, evidence):
"""获取证据的可信度,如果不存在则返回0"""
return self.evidence_cf.get(evidence, 0)
def calculate_conjunction_cf(self, evidence_list):
"""计算合取证据的可信度"""
if not evidence_list:
return 0
return min(self.get_evidence_cf(e) for e in evidence_list)
def calculate_disjunction_cf(self, evidence_list):
"""计算析取证据的可信度"""
if not evidence_list:
return 0
return max(self.get_evidence_cf(e) for e in evidence_list)
def infer(self):
"""进行推理,返回各结论的可信度"""
results = {}
for disease, rule_list in self.rules.items():
disease_cf = 0
for evidence_list, rule_cf in rule_list:
# 计算组合证据的可信度
evidence_cf = self.calculate_conjunction_cf(evidence_list)
# 计算该规则对结论的可信度
cf = rule_cf * evidence_cf
# 组合多个规则的可信度
if cf > 0: # 只考虑支持结论的证据
if disease not in results:
results[disease] = cf
else:
# 多个规则支持同一结论时的合成公式
results[disease] = results[disease] + cf * (1 - results[disease])
# 对结果按可信度排序
return sorted(results.items(), key=lambda x: x[1], reverse=True)
# 使用示例
if __name__ == "__main__":
# 创建可信度系统
cf_system = CertaintyFactorSystem()
# 设置患者症状的可信度
cf_system.set_evidence_cf("发热", 0.9)
cf_system.set_evidence_cf("咳嗽", 0.8)
cf_system.set_evidence_cf("胸痛", 0.7)
cf_system.set_evidence_cf("头痛", 0.4)
cf_system.set_evidence_cf("流鼻涕", 0.5)
# 进行推理
results = cf_system.infer()
# 输出推理结果
print("诊断结果:")
for disease, cf in results:
print(f"{disease}: 可信度 = {cf:.4f}")
可信度方法流程图
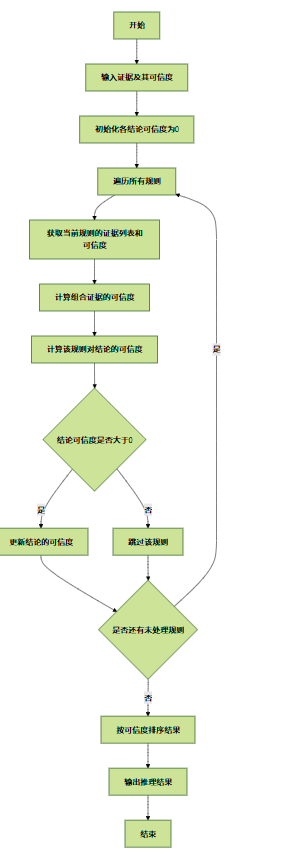
4.3 证据理论
证据理论由 Dempster 提出,Shafer 进一步发展,又称 D-S 理论,是一种处理不确定性的重要方法,尤其适用于多源信息融合。
4.3.1 概率分配函数
设 Ω 为样本空间,函数 m: 2^Ω → [0,1],且满足:
- m(∅) = 0
- ∑{m(A) | A⊆Ω} = 1
则称 m 为 2^Ω 上的概率分配函数,m (A) 为 A 的基本概率数,表示对 A 的精确信任。
4.3.2 信任函数
信任函数 Bel: 2^Ω → [0,1] 定义为:
Bel (A) = ∑{m (B) | B⊆A}
Bel (A) 表示对 A 的总体信任程度。
4.3.3 似然函数
似然函数 Pl: 2^Ω → [0,1] 定义为:
Pl (A) = 1 - Bel (¬A) = ∑{m (B) | B∩A≠∅}
Pl (A) 表示对 A 非假的信任程度,即 A 可能为真的信任程度。
4.3.4 概率分配函数的正交和(证据的组合)
设 m1 和 m2 是两个概率分配函数,其正交和 m = m1 ⊕ m2 定义为:
m (∅) = 0
m (A) = K^(-1) × ∑{m1 (B) × m2 (C) | B∩C=A},其中 K = 1 - ∑{m1 (B) × m2 (C) | B∩C=∅}
4.3.5 基于证据理论的不确定性推理
基于证据理论的推理过程主要包括:
- 建立样本空间
- 获得各个证据的概率分配函数
- 计算信任函数和似然函数
- 用正交和组合各证据的概率分配函数
- 根据组合后的概率分配函数进行决策
证据理论案例与代码实现
下面通过一个多传感器天气判断的例子来实现证据理论:
import numpy as np
class DempsterShaferTheory:
def __init__(self, frame_of_discernment):
"""
初始化证据理论系统
frame_of_discernment: 辨识框架,如['晴天', '多云', '雨天', '雪天']
"""
self.Ω = frame_of_discernment
self.evidence = [] # 存储各个证据的概率分配函数
def add_evidence(self, mass_function):
"""
添加一个证据的概率分配函数
mass_function: 字典,键为辨识框架的子集,值为对应的基本概率数
"""
# 检查概率分配函数的有效性
if sum(mass_function.values()) != 1:
raise ValueError("概率分配函数的和必须为1")
for key in mass_function.keys():
# 检查子集是否合法
if not all(element in self.Ω for element in key):
raise ValueError(f"子集{key}包含不属于辨识框架的元素")
self.evidence.append(mass_function)
def orthogonal_sum(self, m1, m2):
"""计算两个概率分配函数的正交和"""
result = {}
# 计算K值
K = 0
for A, m1_val in m1.items():
for B, m2_val in m2.items():
if set(A).isdisjoint(set(B)): # A和B的交集为空
K += m1_val * m2_val
K = 1 - K
if K == 0:
raise ValueError("证据冲突,无法计算正交和")
# 计算正交和
for A, m1_val in m1.items():
for B, m2_val in m2.items():
intersection = set(A).intersection(set(B))
if intersection:
intersection = tuple(sorted(intersection))
if intersection in result:
result[intersection] += (m1_val * m2_val) / K
else:
result[intersection] = (m1_val * m2_val) / K
return result
def combine_evidence(self):
"""组合所有证据的概率分配函数"""
if not self.evidence:
return {}
result = self.evidence[0].copy()
for i in range(1, len(self.evidence)):
result = self.orthogonal_sum(result, self.evidence[i])
return result
def calculate_belief(self, mass_function, subset):
"""计算子集的信任函数"""
belief = 0
subset = set(subset)
for A, m in mass_function.items():
if set(A).issubset(subset):
belief += m
return belief
def calculate_plausibility(self, mass_function, subset):
"""计算子集的似然函数"""
# 似然函数 = 1 - 信任函数(补集)
complement = set(self.Ω) - set(subset)
if not complement:
return 1.0
# 计算补集的信任函数
belief_complement = 0
for A, m in mass_function.items():
if set(A).issubset(complement):
belief_complement += m
return 1 - belief_complement
def make_decision(self, mass_function):
"""根据概率分配函数做出决策"""
# 对单元素子集的基本概率数进行排序
single_element_masses = {k: v for k, v in mass_function.items() if len(k) == 1}
if not single_element_masses:
return None, 0
decision = max(single_element_masses.items(), key=lambda x: x[1])
return decision
# 使用示例
if __name__ == "__main__":
# 定义辨识框架:天气情况
weather_Ω = ['晴天', '多云', '雨天', '雪天']
# 创建证据理论系统
d_s = DempsterShaferTheory(weather_Ω)
# 添加第一个证据:气象站1的报告
evidence1 = {
('晴天',): 0.5,
('多云',): 0.3,
('雨天',): 0.1,
('雪天',): 0.05,
tuple(weather_Ω): 0.05 # 将列表转换为元组
}
d_s.add_evidence(evidence1)
# 添加第二个证据:气象站2的报告
evidence2 = {
('晴天', '多云'): 0.6,
('雨天',): 0.3,
tuple(weather_Ω): 0.1 # 将列表转换为元组
}
d_s.add_evidence(evidence2)
# 添加第三个证据:卫星云图分析
evidence3 = {
('晴天',): 0.4,
('多云', '雨天'): 0.5,
tuple(weather_Ω): 0.1 # 将列表转换为元组
}
d_s.add_evidence(evidence3)
# 其余代码保持不变...
# 组合所有证据
combined_mass = d_s.combine_evidence()
print("组合后的概率分配函数:")
for key, value in combined_mass.items():
print(f"{key}: {value:.4f}")
# 计算各个天气情况的信任函数和似然函数
print("\n信任函数和似然函数:")
for weather in weather_Ω:
belief = d_s.calculate_belief(combined_mass, (weather,))
plausibility = d_s.calculate_plausibility(combined_mass, (weather,))
print(f"{weather}: Belief = {belief:.4f}, Plausibility = {plausibility:.4f}")
# 做出决策
decision, confidence = d_s.make_decision(combined_mass)
print(f"\n最终决策: 天气最可能是{decision[0]}, 可信度为{confidence:.4f}")

4.4 模糊推理方法
模糊推理是处理模糊性问题的重要方法,能够模拟人类在模糊环境下的思维方式,广泛应用于智能控制、模式识别等领域。
4.4.1 模糊逻辑的提出与发展
模糊逻辑由 Zadeh 于 1965 年提出,旨在处理现实世界中普遍存在的模糊概念,如 "高"、"矮"、"热"、"冷" 等。与传统二值逻辑不同,模糊逻辑允许命题具有介于 0 和 1 之间的真值。
4.4.2 模糊集合
设 U 为论域,模糊集合 A 由隶属度函数 μ_A: U → [0,1] 表示,μ_A (u) 表示元素 u 属于模糊集合 A 的程度。
常见的隶属度函数包括:
- 三角形隶属度函数:μ(x; a, b, c)
- 梯形隶属度函数:μ(x; a, b, c, d)
- 高斯隶属度函数:μ(x; σ, c) = e^(-(x-c)²/(2σ²))
- S 型隶属度函数:μ(x; a, b) = 1/(1 + e^(-a (x-b)))
4.4.3 模糊集合的运算
设 A 和 B 为论域 U 上的模糊集合,隶属度函数分别为 μ_A 和 μ_B:
- 并集:μ_A∪B (x) = max {μ_A (x), μ_B (x)}
- 交集:μ_A∩B (x) = min {μ_A (x), μ_B (x)}
- 补集:μ_¬A (x) = 1 - μ_A (x)
4.4.4 模糊关系与模糊关系的合成
- 模糊关系:论域 U×V 上的模糊集合,用隶属度函数 μ_R (u, v) 表示 u 和 v 之间关系的程度
- 模糊关系的合成:设 R 是 U×V 上的模糊关系,S 是 V×W 上的模糊关系,其合成 R∘S 是 U×W 上的模糊关系,隶属度函数为:
μ_R∘S (u, w) = max_v {min {μ_R (u, v), μ_S (v, w)}}
4.4.5 模糊推理
模糊推理的基本模式是模糊假言推理:
- 大前提:如果 x 是 A,则 y 是 B
- 小前提:x 是 A'
- 结论:y 是 B'
其中 A, A' 是论域 X 上的模糊集合,B, B' 是论域 Y 上的模糊集合。
4.4.6 模糊决策
模糊决策是指在模糊环境下进行决策的过程,主要步骤包括:
- 确定决策目标和评价指标
- 建立模糊评价矩阵
- 确定各指标的权重
- 进行模糊综合评价
- 根据评价结果做出决策
4.4.7 模糊推理的应用
下面通过一个空调温度模糊控制系统的例子来实现模糊推理:
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
class FuzzyController:
def __init__(self):
# 初始化温度论域和隶属度函数参数
self.temperature_universe = np.linspace(10, 40, 101) # 温度论域:10-40℃
self.humidity_universe = np.linspace(20, 90, 101) # 湿度论域:20%-90%
self.fan_speed_universe = np.linspace(0, 100, 101) # 风扇速度论域:0-100%
# 温度模糊集合的参数:冷、适中、热
self.temp_cold = {"type": "triangular", "params": [10, 10, 25]}
self.temp_moderate = {"type": "triangular", "params": [15, 25, 35]}
self.temp_hot = {"type": "triangular", "params": [25, 40, 40]}
# 湿度模糊集合的参数:干燥、适中、潮湿
self.humidity_dry = {"type": "triangular", "params": [20, 20, 50]}
self.humidity_moderate = {"type": "triangular", "params": [30, 50, 70]}
self.humidity_潮湿 = {"type": "triangular", "params": [50, 90, 90]}
# 风扇速度模糊集合的参数:慢、中、快
self.fan_slow = {"type": "triangular", "params": [0, 0, 30]}
self.fan_medium = {"type": "triangular", "params": [20, 50, 80]}
self.fan_fast = {"type": "triangular", "params": [70, 100, 100]}
# 模糊控制规则
self.rules = [
# 温度冷
{"temp": "cold", "humidity": "dry", "fan": "slow"},
{"temp": "cold", "humidity": "moderate", "fan": "slow"},
{"temp": "cold", "humidity": "潮湿", "fan": "medium"},
# 温度适中
{"temp": "moderate", "humidity": "dry", "fan": "slow"},
{"temp": "moderate", "humidity": "moderate", "fan": "medium"},
{"temp": "moderate", "humidity": "潮湿", "fan": "fast"},
# 温度热
{"temp": "hot", "humidity": "dry", "fan": "medium"},
{"temp": "hot", "humidity": "moderate", "fan": "fast"},
{"temp": "hot", "humidity": "潮湿", "fan": "fast"}
]
def membership_function(self, x, mf_type, params):
"""计算隶属度函数值"""
if mf_type == "triangular":
a, b, c = params
if x <= a:
return 0
elif a < x <= b:
return (x - a) / (b - a)
elif b < x <= c:
return (c - x) / (c - b)
else:
return 0
elif mf_type == "gaussian":
sigma, c = params
return np.exp(-((x - c) ** 2) / (2 * sigma ** 2))
else:
raise ValueError(f"不支持的隶属度函数类型: {mf_type}")
def fuzzify(self, value, universe, mf_dict):
"""模糊化:将精确值转换为模糊集合的隶属度"""
result = {}
for name, mf in mf_dict.items():
memberships = [self.membership_function(x, mf["type"], mf["params"]) for x in universe]
# 计算该值在模糊集合中的隶属度
mu = self.membership_function(value, mf["type"], mf["params"])
result[name] = mu
return result
def apply_rules(self, temp_fuzzy, humidity_fuzzy):
"""应用模糊规则,得到风扇速度的模糊集合"""
fan_fuzzy = {
"slow": 0,
"medium": 0,
"fast": 0
}
for rule in self.rules:
# 计算规则前件的满足度
temp_mu = temp_fuzzy[rule["temp"]]
humidity_mu = humidity_fuzzy[rule["humidity"]]
antecedent_strength = min(temp_mu, humidity_mu) # 取小运算
# 更新后件的隶属度
fan_fuzzy[rule["fan"]] = max(fan_fuzzy[rule["fan"]], antecedent_strength)
return fan_fuzzy
def defuzzify(self, fan_fuzzy, universe, mf_dict):
"""去模糊化:将模糊集合转换为精确值(重心法)"""
numerator = 0
denominator = 0
for fan_speed in universe:
# 计算该速度在各模糊集合中的隶属度
mu = 0
for name, mf in mf_dict.items():
if fan_fuzzy[name] > 0:
mu = max(mu, min(fan_fuzzy[name], self.membership_function(fan_speed, mf["type"], mf["params"])))
numerator += fan_speed * mu
denominator += mu
if denominator == 0:
return 0
return numerator / denominator
def control(self, temperature, humidity):
"""模糊控制主函数"""
# 模糊化
temp_fuzzy = self.fuzzify(temperature, self.temperature_universe, {
"cold": self.temp_cold,
"moderate": self.temp_moderate,
"hot": self.temp_hot
})
humidity_fuzzy = self.fuzzify(humidity, self.humidity_universe, {
"dry": self.humidity_dry,
"moderate": self.humidity_moderate,
"潮湿": self.humidity_潮湿
})
# 应用规则
fan_fuzzy = self.apply_rules(temp_fuzzy, humidity_fuzzy)
# 去模糊化
fan_speed = self.defuzzify(fan_fuzzy, self.fan_speed_universe, {
"slow": self.fan_slow,
"medium": self.fan_medium,
"fast": self.fan_fast
})
return fan_speed, temp_fuzzy, humidity_fuzzy, fan_fuzzy
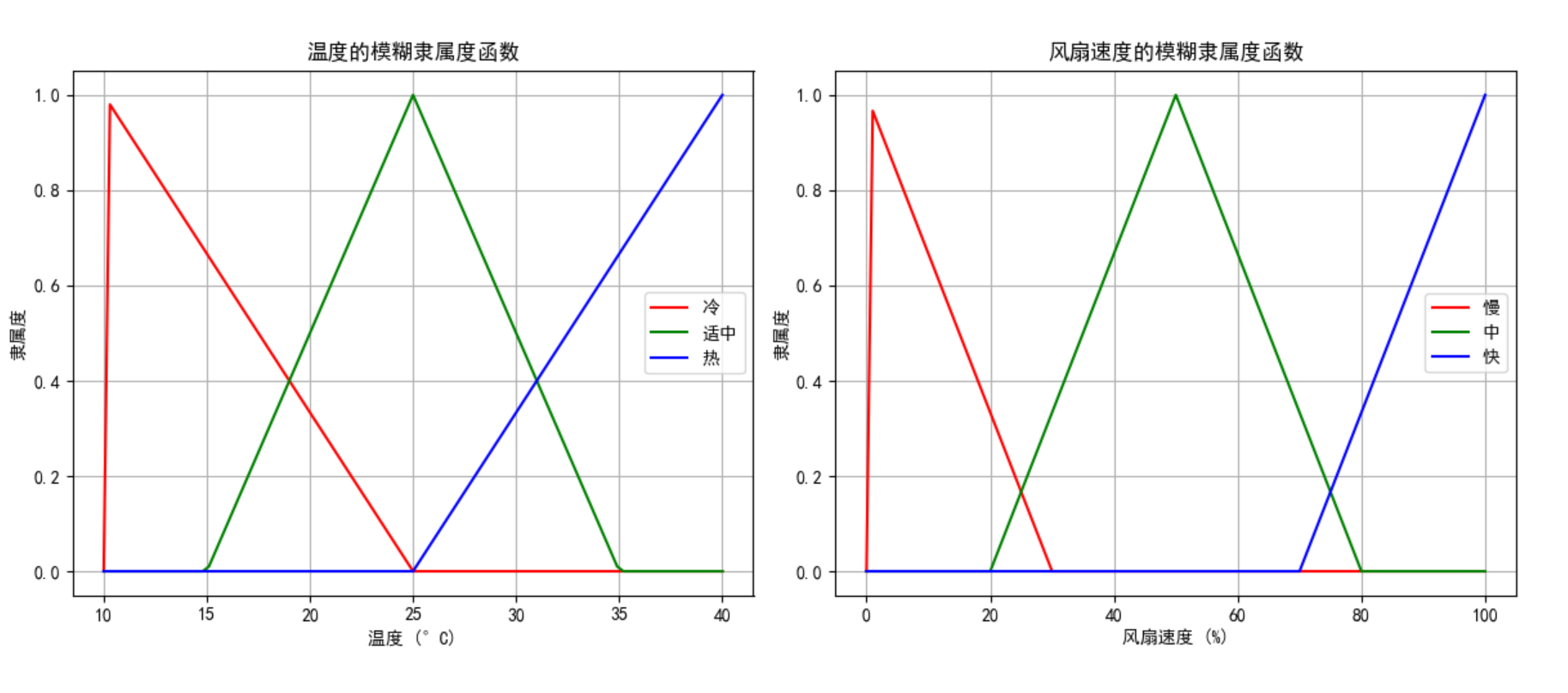
def plot_membership_functions(self):
"""绘制温度和风扇速度的隶属度函数"""
plt.figure(figsize=(12, 5))
# 绘制温度隶属度函数
plt.subplot(1, 2, 1)
plt.plot(self.temperature_universe,
[self.membership_function(x, self.temp_cold["type"], self.temp_cold["params"]) for x in
self.temperature_universe], 'r-', label='冷')
plt.plot(self.temperature_universe,
[self.membership_function(x, self.temp_moderate["type"], self.temp_moderate["params"]) for x in
self.temperature_universe], 'g-', label='适中')
plt.plot(self.temperature_universe,
[self.membership_function(x, self.temp_hot["type"], self.temp_hot["params"]) for x in
self.temperature_universe], 'b-', label='热')
plt.xlabel('温度 (°C)')
plt.ylabel('隶属度')
plt.title('温度的模糊隶属度函数')
plt.legend()
plt.grid(True)
# 绘制风扇速度隶属度函数
plt.subplot(1, 2, 2)
plt.plot(self.fan_speed_universe,
[self.membership_function(x, self.fan_slow["type"], self.fan_slow["params"]) for x in
self.fan_speed_universe], 'r-', label='慢')
plt.plot(self.fan_speed_universe,
[self.membership_function(x, self.fan_medium["type"], self.fan_medium["params"]) for x in
self.fan_speed_universe], 'g-', label='中')
plt.plot(self.fan_speed_universe,
[self.membership_function(x, self.fan_fast["type"], self.fan_fast["params"]) for x in
self.fan_speed_universe], 'b-', label='快')
plt.xlabel('风扇速度 (%)')
plt.ylabel('隶属度')
plt.title('风扇速度的模糊隶属度函数')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.savefig('fuzzy_membership_functions.png')
plt.show()
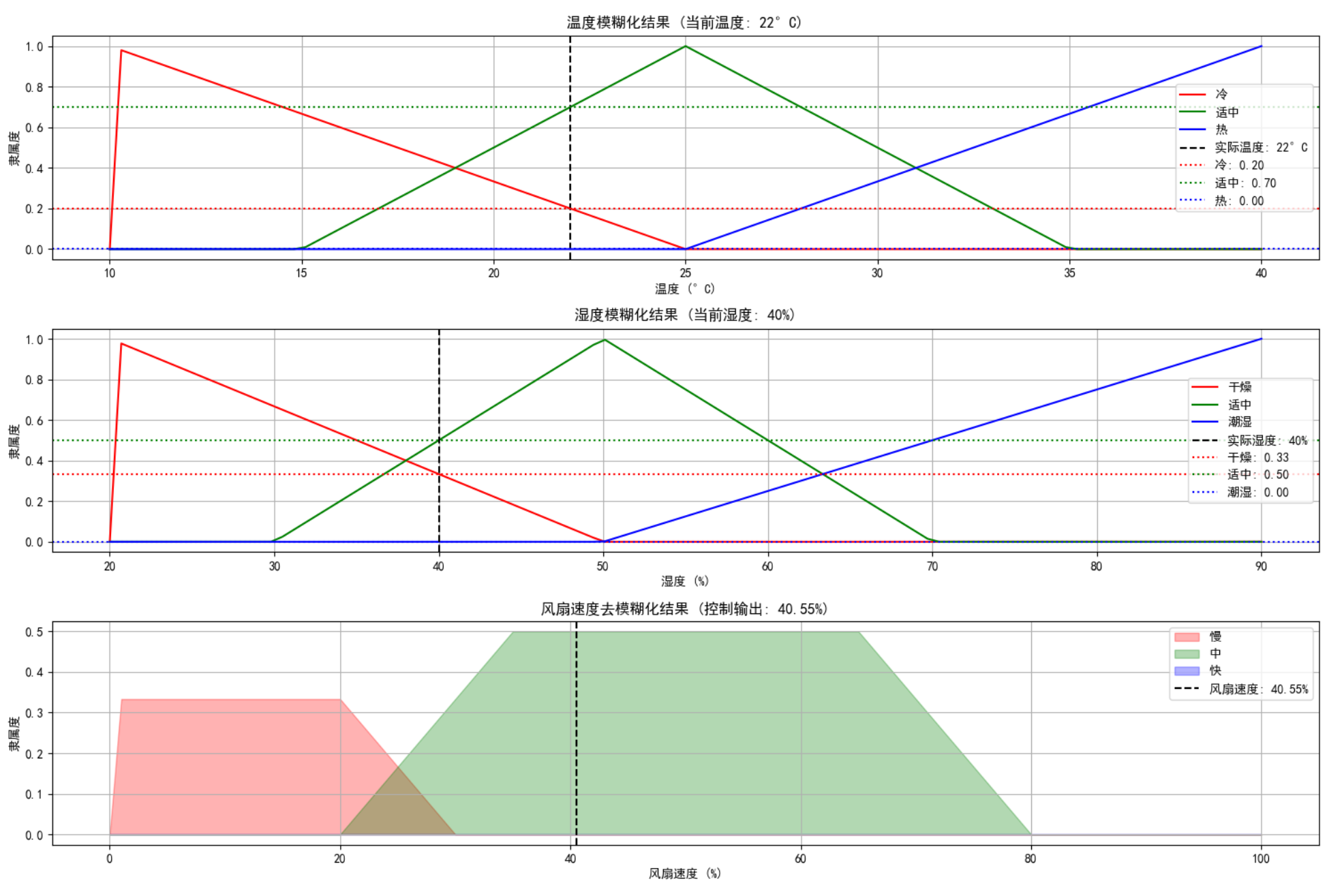
def plot_fuzzy_control_process(self, temperature, humidity):
"""绘制模糊控制过程"""
fan_speed, temp_fuzzy, humidity_fuzzy, fan_fuzzy = self.control(temperature, humidity)
plt.figure(figsize=(15, 10))
# 绘制温度模糊化结果
plt.subplot(3, 1, 1)
plt.plot(self.temperature_universe,
[self.membership_function(x, self.temp_cold["type"], self.temp_cold["params"]) for x in
self.temperature_universe], 'r-', label='冷')
plt.plot(self.temperature_universe,
[self.membership_function(x, self.temp_moderate["type"], self.temp_moderate["params"]) for x in
self.temperature_universe], 'g-', label='适中')
plt.plot(self.temperature_universe,
[self.membership_function(x, self.temp_hot["type"], self.temp_hot["params"]) for x in
self.temperature_universe], 'b-', label='热')
plt.axvline(x=temperature, color='k', linestyle='--', label=f'实际温度: {temperature}°C')
plt.axhline(y=temp_fuzzy["cold"], color='r', linestyle=':', label=f'冷: {temp_fuzzy["cold"]:.2f}')
plt.axhline(y=temp_fuzzy["moderate"], color='g', linestyle=':', label=f'适中: {temp_fuzzy["moderate"]:.2f}')
plt.axhline(y=temp_fuzzy["hot"], color='b', linestyle=':', label=f'热: {temp_fuzzy["hot"]:.2f}')
plt.xlabel('温度 (°C)')
plt.ylabel('隶属度')
plt.title(f'温度模糊化结果 (当前温度: {temperature}°C)')
plt.legend()
plt.grid(True)
# 绘制湿度模糊化结果
plt.subplot(3, 1, 2)
plt.plot(self.humidity_universe,
[self.membership_function(x, self.humidity_dry["type"], self.humidity_dry["params"]) for x in
self.humidity_universe], 'r-', label='干燥')
plt.plot(self.humidity_universe,
[self.membership_function(x, self.humidity_moderate["type"], self.humidity_moderate["params"]) for x in
self.humidity_universe], 'g-', label='适中')
plt.plot(self.humidity_universe,
[self.membership_function(x, self.humidity_潮湿["type"], self.humidity_潮湿["params"]) for x in
self.humidity_universe], 'b-', label='潮湿')
plt.axvline(x=humidity, color='k', linestyle='--', label=f'实际湿度: {humidity}%')
plt.axhline(y=humidity_fuzzy["dry"], color='r', linestyle=':', label=f'干燥: {humidity_fuzzy["dry"]:.2f}')
plt.axhline(y=humidity_fuzzy["moderate"], color='g', linestyle=':',
label=f'适中: {humidity_fuzzy["moderate"]:.2f}')
plt.axhline(y=humidity_fuzzy["潮湿"], color='b', linestyle=':', label=f'潮湿: {humidity_fuzzy["潮湿"]:.2f}')
plt.xlabel('湿度 (%)')
plt.ylabel('隶属度')
plt.title(f'湿度模糊化结果 (当前湿度: {humidity}%)')
plt.legend()
plt.grid(True)
# 绘制风扇速度去模糊化结果
plt.subplot(3, 1, 3)
x = self.fan_speed_universe
slow = [min(fan_fuzzy["slow"], self.membership_function(s, self.fan_slow["type"], self.fan_slow["params"])) for
s in x]
medium = [
min(fan_fuzzy["medium"], self.membership_function(s, self.fan_medium["type"], self.fan_medium["params"]))
for s in x]
fast = [min(fan_fuzzy["fast"], self.membership_function(s, self.fan_fast["type"], self.fan_fast["params"])) for
s in x]
plt.fill_between(x, slow, color='r', alpha=0.3, label='慢')
plt.fill_between(x, medium, color='g', alpha=0.3, label='中')
plt.fill_between(x, fast, color='b', alpha=0.3, label='快')
plt.axvline(x=fan_speed, color='k', linestyle='--', label=f'风扇速度: {fan_speed:.2f}%')
plt.xlabel('风扇速度 (%)')
plt.ylabel('隶属度')
plt.title(f'风扇速度去模糊化结果 (控制输出: {fan_speed:.2f}%)')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.savefig(f'fuzzy_control_process_{temperature}_{humidity}.png')
plt.show()
# 使用示例
if __name__ == "__main__":
# 创建模糊控制器
controller = FuzzyController()
# 绘制隶属度函数
controller.plot_membership_functions()
# 测试不同温度和湿度下的控制效果
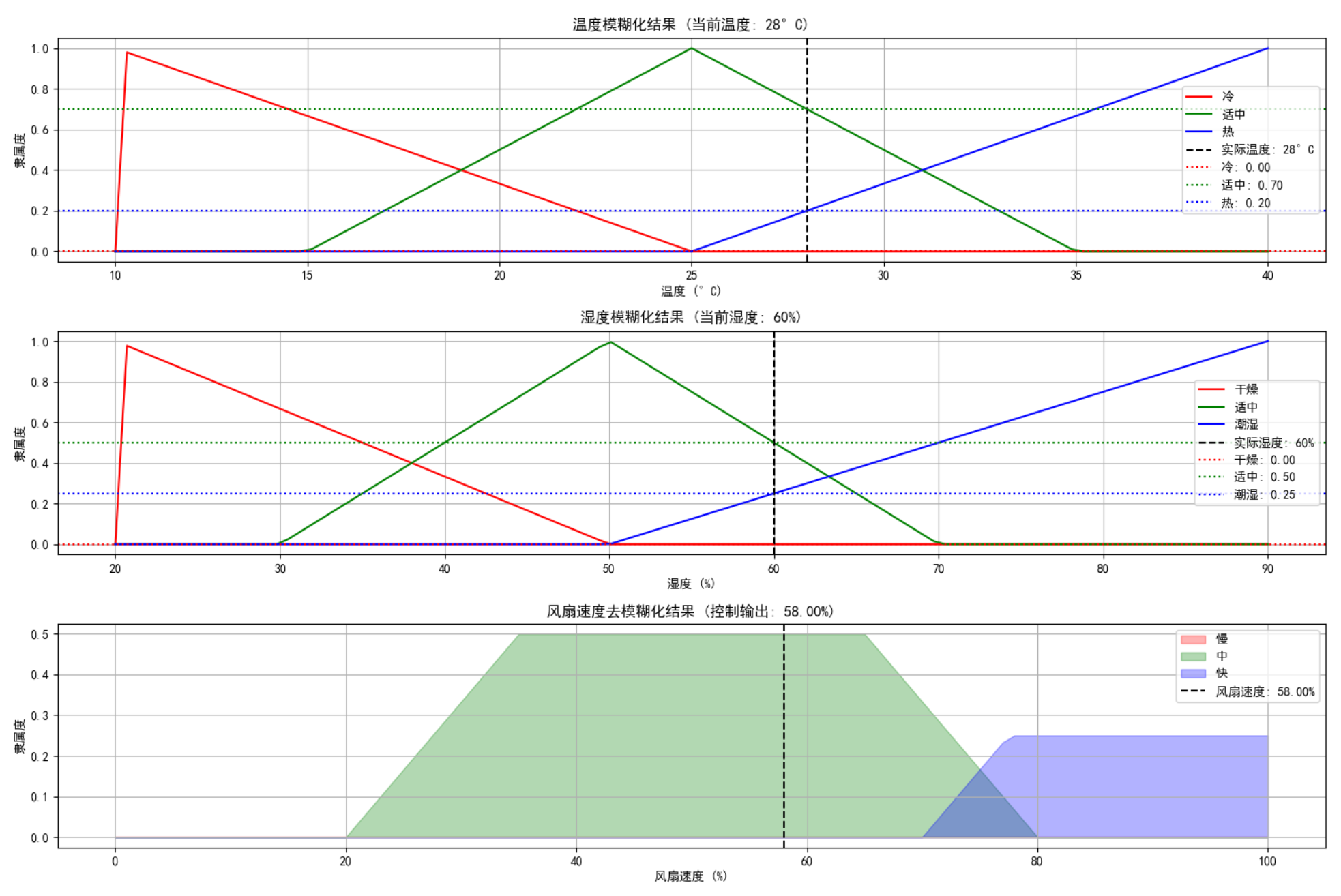
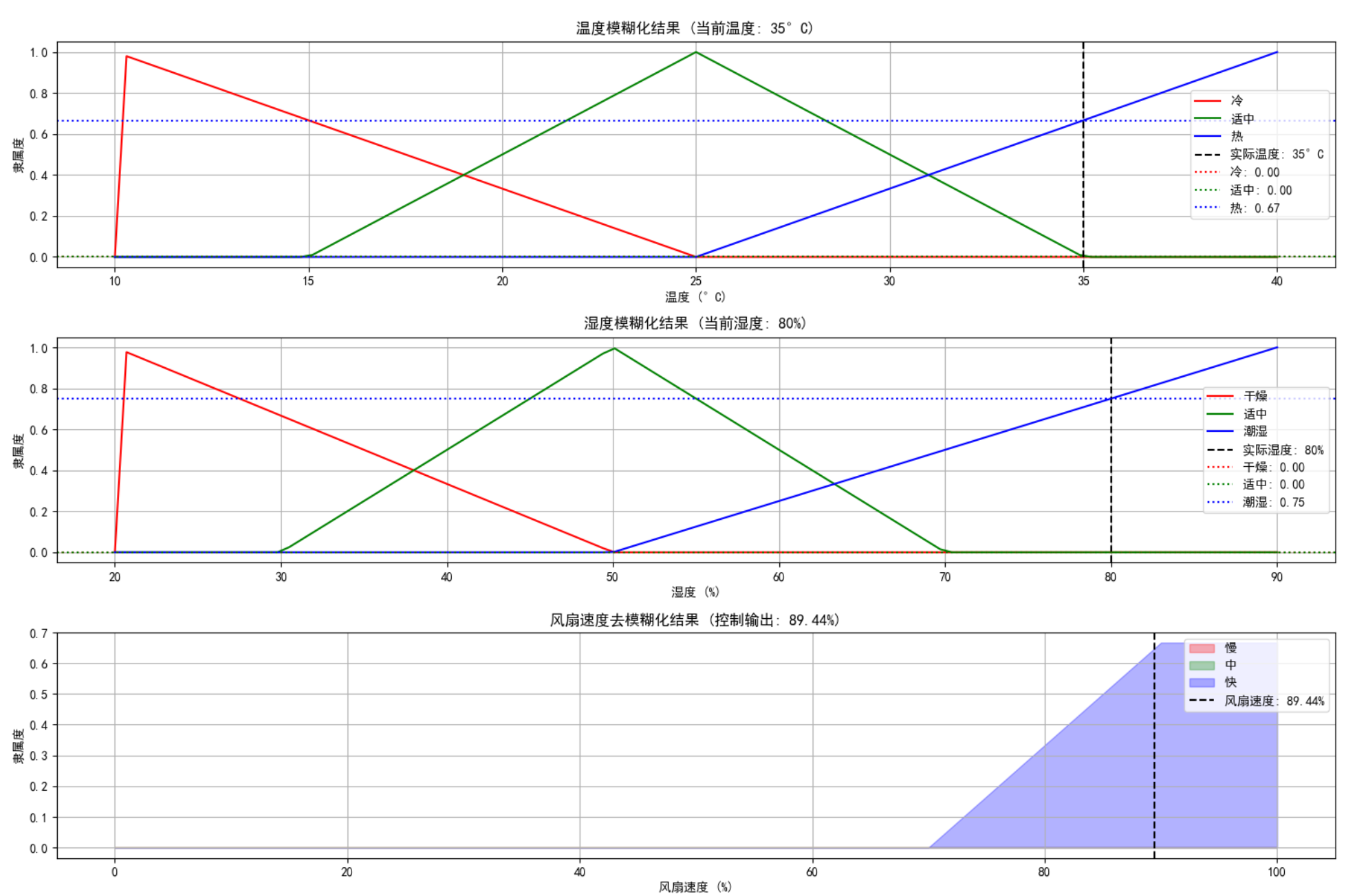
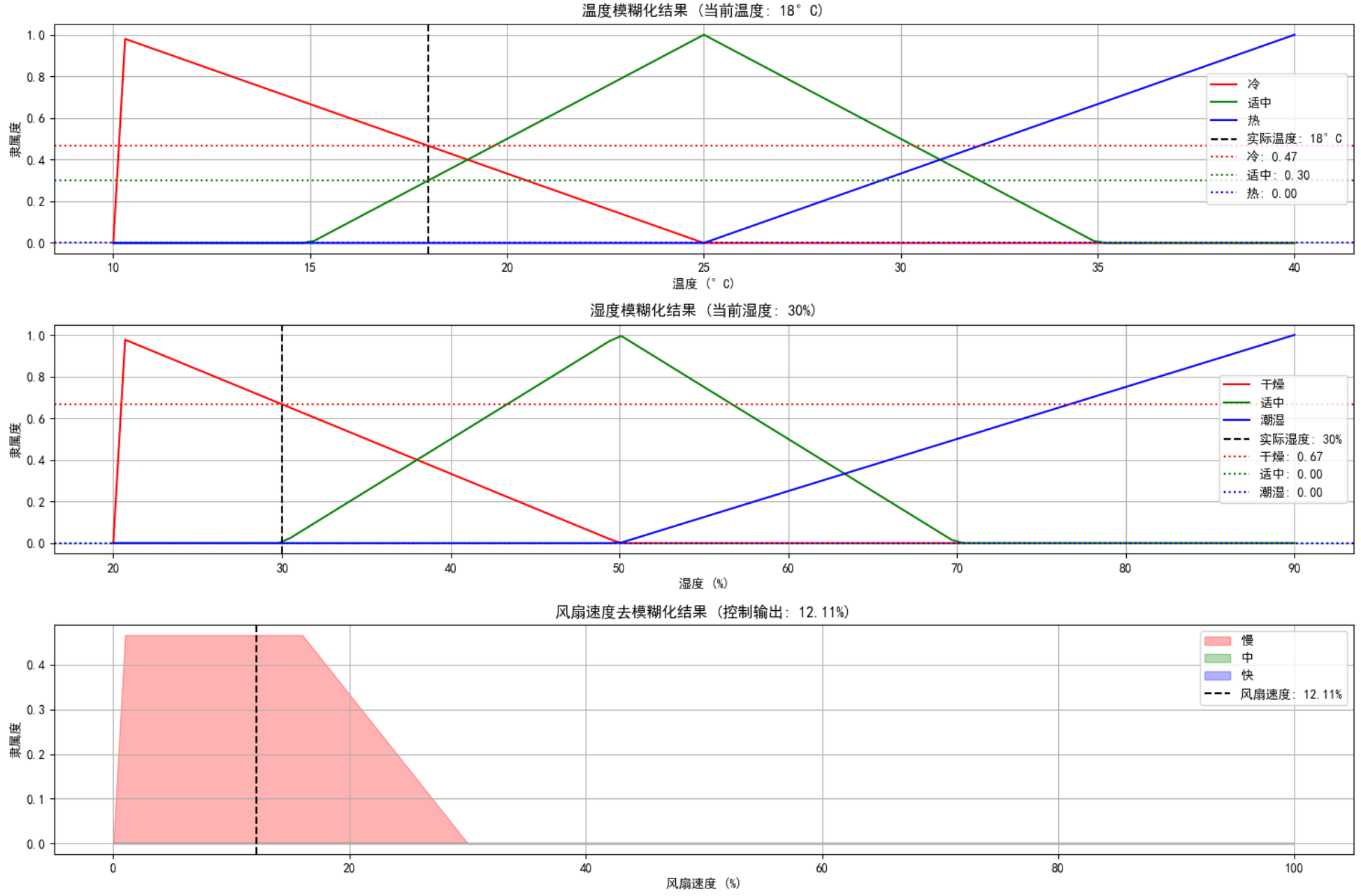
test_cases = [(22, 40), (28, 60), (35, 80), (18, 30)]
for temp, humidity in test_cases:
print(f"当前温度: {temp}°C, 湿度: {humidity}%")
fan_speed, _, _, _ = controller.control(temp, humidity)
print(f"建议风扇速度: {fan_speed:.2f}%\n")
controller.plot_fuzzy_control_process(temp, humidity)
模糊推理流程图
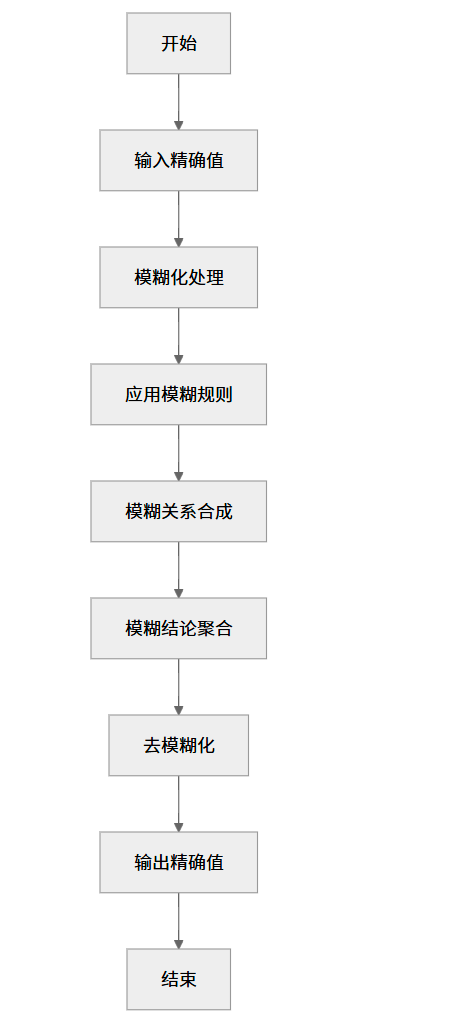
4.5 小结
本章详细介绍了人工智能中处理不确定性的三种重要方法:可信度方法、证据理论和模糊推理方法。
-
可信度方法基于确定性理论,通过可信度因子表示不确定性,计算简单直观,适用于专家系统等领域。
-
证据理论通过概率分配函数、信任函数和似然函数来处理不确定性,能够有效组合多源证据,适用于多传感器融合等场景。
-
模糊推理方法通过模糊集合和隶属度函数处理模糊性问题,能够模拟人类的模糊思维,广泛应用于智能控制、决策分析等领域。
每种方法都有其独特的优势和适用场景,在实际应用中,可根据问题的特点选择合适的不确定性推理方法,或结合多种方法以获得更好的效果。
总结与实践建议
不确定性推理是人工智能领域的核心问题之一,掌握这些方法对于开发实际的智能系统至关重要。建议读者通过以下方式加深理解:
- 动手实现本章的代码案例,尝试修改参数观察结果变化
- 寻找实际生活中的不确定性问题,尝试用本章方法建模解决
- 阅读相关文献,了解这些方法的最新发展和应用
- 比较不同方法的优缺点,思考如何结合多种方法处理复杂问题
通过理论学习和实践操作的结合,能够更好地掌握不确定性推理方法,为开发更智能、更鲁棒的人工智能系统奠定基础。























 1953
1953

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








