NO.2 《机器学习期末复习篇》以题（问答题）促习（人学习），满满干huo，大胆学大胆补！

本文链接：https://blog.youkuaiyun.com/2302_80644606/article/details/144012610

一、试根据以下数据使用最小二乘估计确定房价与其位置之间的大致关系。

现有一组某市的房价与其位置数据如表 2-12 所示，其中 D 表示房屋到市中心的直线距离，单位为 km，R 表示房屋单价，单位为元/m²。

表 2-12 房价与其位置数据表

序号	1	2	3	4	5	6	7	8	9
D/km	4.2	7.1	6.3	1.1	0.2	4.0	3.5	8	2.3
R/(元/m²)	8600	6100	6700	12000	14200	8500	8900	6200	11200

设定模型： 我们假设房价和距离之间的关系是线性的：

其中：
- a 是房价对距离的斜率，表示距离每增加 1 km，房价的变化。
- b 是截距，表示距离市中心为 0 时的房价。
最小二乘法公式： 最小二乘法的核心是找到 a 和 b，使得预测值和实际值之间的误差平方和最小化。公式为：
- n是数据点个数（这里 n=9）。
- $D_i$ 和 $R_i$ 分别是第 i 个数据点的距离和房价。
其中：
计算中间值： 根据公式，我们需要计算：
- $\sum D_i$ ：距离的总和。
- $\sum R_i$ ：房价的总和。
- $\sum D_i^2$ ：距离平方的总和。
- $\sum (D_i \cdot R_i)$ ：距离和房价的乘积的总和。

计算过程

我们将表格补充中间值，进行计算：

序号	$D_i$ (km)	$R_i$ (元/m²)	$\sum D_i^2$	$\sum (D_i \cdot R_i)$
1	4.2	8600	17.64	36120
2	7.1	6100	50.41	43310
3	6.3	6700	39.69	42210
4	1.1	12000	1.21	13200
5	0.2	14200	0.04	2840
6	4.0	8500	16.00	34000
7	3.5	8900	12.25	31150
8	8.0	6200	64.00	49600
9	2.3	11200	5.29	25760

接下来，我们计算求和：

$\sum D_i = 4.2 + 7.1 + 6.3 + 1.1 + 0.2 + 4.0 + 3.5 + 8.0 + 2.3 = 36.7$
$\sum R_i = 8600 + 6100 + 6700 + 12000 + 14200 + 8500 + 8900 + 6200 + 11200 = 82400$
$\sum D_i^2 = 17.64 + 50.41 + 39.69 + 1.21 + 0.04 + 16.00 + 12.25 + 64.00 + 5.29 = 206.53$
$\sum (D_i R_i) = 36120 + 43310 + 42210 + 13200 + 2840 + 34000 + 31150 + 49600 + 25760 = 248190$

代入公式计算 a和 b

现在将上述值代入最小二乘法公式：

得出模型：

最终的房价与距离关系为：

结果：

a=−1546：每远离市中心 1 km，房价平均下降 1546 元/m²。
b=15407：市中心（距离 D=0）的房价估计为 15407 元/m²。

可视化

二、试通过表中数据使用最大似然估计法估计 $\mu$ 和 $\sigma_2$ 的取值。（单位：cm）

最大似然估计讲的太高级，其实就是知道数据，然后要让能够观测到这些数据的概率最大化

公式的话：就是一个求均值，一个求偏方差

假设某学校男生的身高服从正态分布 N(μ,σ2)，现从全校所有男生中随机采样测量得到身高数据如表 2-13 所示

表 2-13 身高数据表

序号	1	2	3	4	5	6	7	8
身高	167	175	163	169	174	187	168	176

正态分布的概率密度函数为：

最大似然估计原理：给定样本数据 $x_1,x_2,x_3....x_n$ ，最大似然估计通过最大化样本数据联合概率（似然函数）来估计参数。

似然函数 $L(\mu, \sigma^2)$ 为：

（1）取对数，得到对数似然函数：

（2）对 $\mu$ 求偏导，令其等于 0：

$\frac{\partial \ln L}{\partial \mu} = \frac{1}{\sigma^2} \sum_{i=1}^n (x_i - \mu) = 0$

样本均值是 $\mu$ 的最大似然估计值

（3）对 $\sigma$ 求偏导，令其等于 0：

（4）得到：

数据如下：
$x=[167,175,163,169,174,187,168,176]$
样本大小：
n=8
计算均值 $\mu$ ：
$\mu = \frac{1}{n} \sum_{i=1}^n x_i = \frac{167 + 175 + 163 + 169 + 174 + 187 + 168 + 176}{8}$ $\mu = \frac{1379}{8} = 172.375$
计算方差 $\sigma^2$ ： 先计算每个样本与均值的差平方：

差平方结果：

然后求和并除以样本大小 n：

让我们计算并展示最终结果。

通过计算得到：

均值 $\mu$ ： 172.375 cm
方差 $\sigma^2$ ： 47.984 cm²

三、试根据表 2-13 中数据和最大后验估计法确定 $\mu$ 和 $\sigma_2$ 的估计值。

假设某学校男生的身高服从正态分布 N(μ,σ2)，上一次测试时得到身高均值的估计值为 172 cm，方差为 36。故在本次测试前，以 0.7 的概率相信该校男生身高服从 N(172,36)。

先验分布（Prior Distribution）
根据题意，上一次的测试结果表明：

且先验权重为 0.7（即我们对先验分布有较高的置信度）。
似然函数（Likelihood Function）
表 2-13 的数据代表样本，假设其服从正态分布 $N(\mu, \sigma^2)$ ：
- 样本数据 $x=[167,175,163,169,174,187,168,176]$
- 样本大小 n=8
- 样本均值： $\bar{x} = \frac{1}{n} \sum_{i=1}^n x_i$
- 样本方差： $s^2 = \frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})^2$
后验分布（Posterior Distribution）
根据贝叶斯定理，结合先验分布和似然函数，后验分布为：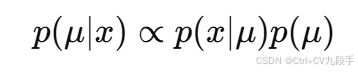

最大后验估计（MAP）通过最大化后验分布，来估计 $\mu$ 和 $\sigma^2$ 。
最大后验估计公式
- 均值 μ的 MAP 估计：其中 α=0.7是先验权重。
- 方差 $\sigma^2$ 的 MAP 估计：在 MAP 方法中， $\sigma^2$ 的估计需要结合样本方差和先验分布。公式为：

计算步骤

1. 样本均值和方差

计算样本均值 $\bar{x}$ 和样本方差 $s^2$ ：

2. MAP 均值估计 $\hat{\mu}$

将 $\mu_0 = 172$ 、 $\sigma_0^2 = 36$ 、先验权重 $\alpha = 0.7$ 、样本数据代入公式：

3. MAP 方差估计 $\hat{\sigma}^2$

代入数据计算：

让我们一步步计算得到结果。

通过最大后验估计法（MAP），得到男生身高分布参数的估计值为：

均值 $\hat{\mu} = 172.34 \, \text{cm}$
方差 $\hat{\sigma}^2 = 44.13 \, \text{cm}^2$

四、试用梯度下降算法求解无约束非线性规划问题

其中， $\mathbf{X}=(x_1,x_2)^T$ ，要求选取初始点 $X_0=(0,3)^T$ ，终止误差 $\varepsilon =0.1$ 。

梯度下降法是迭代优化方法，其核心是沿目标函数的负梯度方向更新解：

其中：

$\nabla f(X)$ 是目标函数的梯度。
$\alpha$ 是学习率（步长）。
迭代停止条件： $\|\nabla f(X^k)\| < \epsilon$

计算目标函数的梯度

迭代过程

初始点： $X^0 = (0, 3)^T$
计算梯度 $\nabla f(X^k)$
更新公式：

检查停止条件： $\|\nabla f(X^k)\| < \epsilon=0.1$

让我们选择一个合适的学习率 α，并开始计算迭代过程。

通过梯度下降法计算，得到的结果为：

该解满足终止条件 $\|\nabla f(X^k)\| < \epsilon=0.1$ 。

代码：

import numpy as np

# Define the objective function and its gradient
def f(X):
    x1, x2 = X
    return (x1 - 2)**4 + (x1 - 2*x2)**2

def grad_f(X):
    x1, x2 = X
    df_dx1 = 4 * (x1 - 2)**3 + 2 * (x1 - 2 * x2)
    df_dx2 = -4 * (x1 - 2 * x2)
    return np.array([df_dx1, df_dx2])

# Gradient descent parameters
X = np.array([0, 3])  # Initial point
epsilon = 0.1  # Stopping criterion
alpha = 0.01  # Learning rate
iterations = 0  # Iteration counter

# Gradient descent loop
while np.linalg.norm(grad_f(X)) >= epsilon:
    X = X - alpha * grad_f(X)  # Update rule
    iterations += 1

X, f(X), iterations

可视化：

背景等高线：目标函数 f(X) 的值，越靠近中心越接近最优解。
红色路径：梯度下降的优化路径，从初始点 (0,3)开始逐步向最优解收敛。
蓝点：最终的最优解 (1.83,0.92)。

五、计算前两次迭代的结果

若要使用表 2-12 中的数据构造一个用于预测房屋价格与房屋到市区距离之间关系的线性模型，其中模型优化过程使用梯度下降算法，试取任意初始点开始迭代，步长取 0.05，计算前两次迭代的结果。

线性模型
假设房价 R和距离 D 的关系为：

目标是通过梯度下降法优化模型参数 a和 b。
损失函数
损失函数采用均方误差（MSE）：
梯度计算
对损失函数分别对 a 和 b 求偏导数：
参数更新公式
使用梯度下降法更新 a 和 b：

其中 α是学习率。
代码

# Data from Table 2-12
D = np.array([4.2, 7.1, 6.3, 1.1, 0.2, 4.0, 3.5, 8.0, 2.3])  # Distances
R = np.array([8600, 6100, 6700, 12000, 14200, 8500, 8900, 6200, 11200])  # Prices

# Initialize parameters
a = 0  # Initial value for slope
b = 0  # Initial value for intercept
alpha = 0.05  # Learning rate
n = len(D)  # Number of data points

# Function to compute gradients
def compute_gradients(a, b, D, R):
    da = -(1 / n) * np.sum(D * (R - (a * D + b)))  # Gradient for a
    db = -(1 / n) * np.sum(R - (a * D + b))        # Gradient for b
    return da, db

# Store results for the first two iterations
results = []
for i in range(2):  # Compute two iterations
    da, db = compute_gradients(a, b, D, R)  # Compute gradients
    a = a - alpha * da                      # Update a
    b = b - alpha * db                      # Update b
    results.append((a, b))                  # Store updated parameters

results

得到结果：

六、与共轭梯度法相比较，梯度下降法有何缺陷？共轭梯度法为何能避免这种缺陷？

特性	梯度下降法	共轭梯度法
方向选择	沿负梯度方向	沿共轭方向（结合前几步信息）
收敛速度	慢，可能震荡	快，避免震荡
学习率依赖	需要选择学习率，调试较复杂	自动线搜索，无需人工调整
适用场景	简单问题或小规模优化	大规模、复杂或条件数较大问题

梯度下降法的缺陷

收敛速度慢：
- 梯度下降法沿当前梯度的负方向更新参数，但在复杂情况下，尤其是目标函数的等高线呈长条形（条件数较大）时，梯度下降会呈现“锯齿”状的前进轨迹，导致收敛速度非常慢。
- 当函数的二次曲面有陡峭和扁平方向（如椭圆形等高线）时，梯度下降可能需要大量的迭代才能到达最优点。
学习率依赖性强：
- 梯度下降法对学习率（步长）敏感，学习率过大会导致发散，过小则收敛缓慢。
- 通常需要人工调节学习率，这增加了使用的难度。
无法保证避免局部极值点：梯度下降法可能会陷入局部最优点（对于非凸函数），而无法保证找到全局最优解。

共轭梯度法的优势

共轭梯度法通过引入共轭方向解决了梯度下降法的上述问题，特别是在处理二次优化问题时效果显著。

共轭方向减少重复计算：
- 共轭梯度法在每次迭代时不是简单地沿梯度方向前进，而是选择一种新的搜索方向，该方向与前面的搜索方向是共轭的。
- 共轭的意义是使得每次更新后，新的方向对之前的方向是正交的，在二次曲面问题上，最多经过 nnn 次迭代即可到达最优点（理论上）。
收敛速度快：
- 共轭梯度法通过结合前几次迭代的信息，能更快地沿函数曲面移动到全局最优点，避免了梯度下降中“锯齿状”震荡的问题。
- 特别适用于目标函数的等高线呈现长条形时，收敛速度远远快于梯度下降。
无需选择学习率：共轭梯度法在每次迭代中使用线搜索自动选择最优步长，从而避免了梯度下降法中手动调整学习率的问题。

七、利用共轭梯度算法求解无约束非线性规划问题

其中， $X=(x_1,x_2)^T$ ，取迭代起始点为 $X_0=(1,1)^T$ 。

目标函数：

其中

初始点：

共轭梯度法特点：

共轭梯度法的核心是以共轭方向作为搜索方向，可以快速找到目标函数的极小值。
更新公式：其中：
- $P^k$ 是第 k 步的搜索方向。
- $\alpha_k$ 是步长，通过线搜索确定。
- H是海森矩阵
搜索方向更新公式：
其中：
- ∇f(X)是梯度向量。

梯度计算

目标函数：

梯度为：

# Define the gradient and Hessian of the function
def gradient(X):
    x1, x2 = X
    df_dx1 = 1 + 4 * x1 + 2 * x2
    df_dx2 = -1 + 2 * x1 + 2 * x2
    return np.array([df_dx1, df_dx2])

def hessian():
    # Hessian matrix of the quadratic function
    return np.array([[4, 2], [2, 2]])

# Initialize variables
X = np.array([1, 1])  # Starting point
grad = gradient(X)    # Initial gradient
P = -grad             # Initial search direction (negative gradient)
H = hessian()         # Hessian matrix

# Store results for the first two iterations
results = []
for _ in range(2):
    # Compute step size alpha_k
    alpha = -(grad @ P) / (P @ H @ P)
    # Update X
    X_new = X + alpha * P
    # Store the result
    results.append((X_new, alpha))
    # Compute new gradient
    grad_new = gradient(X_new)
    # Compute beta_k
    beta = (grad_new @ grad_new) / (grad @ grad)
    # Update search direction
    P = -grad_new + beta * P
    # Update X and gradient for next iteration
    X, grad = X_new, grad_new

results

得到结果：

八、计算前两次迭代的结果

若要使用表 2-12 中的数据构造一个用于预测房屋价格与房屋到市区距离之间关系的线性模型，其中模型优化过程使用共轭梯度法，试取任意初始点开始迭代，计算前两次迭代的结果。

目标

根据表 2-12 中的数据，构建一个线性模型：

$R=aD+b$

其中：

R为房价。
D 为距离市中心的距离。
a 和 b 为模型参数。

优化方法

通过共轭梯度法优化损失函数：

这里，损失函数是均方误差（MSE），且目标是找到参数 a和 b 使得 J(a,b) 最小。

共轭梯度法流程

损失函数梯度：梯度对参数 a 和 b的形式为：
Hessian矩阵：目标函数 J(a,b)为二次型函数，其 Hessian 矩阵为：

对于线性回归模型的 MSE：
迭代更新公式：

已知数据

让我们计算结果。

通过共轭梯度法计算得到前两次迭代结果如下：

# Re-importing necessary libraries
import numpy as np

# Data from Table 2-12
D = np.array([4.2, 7.1, 6.3, 1.1, 0.2, 4.0, 3.5, 8.0, 2.3])  # Distances
R = np.array([8600, 6100, 6700, 12000, 14200, 8500, 8900, 6200, 11200])  # Prices
n = len(D)

# Initial parameters
a, b = 0, 0  # Starting point
X = np.array([a, b])  # Parameter vector

# Hessian matrix
H = (1 / n) * np.array([
    [np.sum(D**2), np.sum(D)],
    [np.sum(D), n]
])

# Gradient function
def gradient(X):
    a, b = X
    da = -(1 / n) * np.sum(D * (R - (a * D + b)))
    db = -(1 / n) * np.sum(R - (a * D + b))
    return np.array([da, db])

# Store results for first two iterations
results = []

# Initial gradient and search direction
grad = gradient(X)
P = -grad

# Perform two iterations of conjugate gradient method
for _ in range(2):
    # Step size alpha
    alpha = -(grad @ P) / (P @ H @ P)
    # Update parameters
    X_new = X + alpha * P
    # Store the result
    results.append((X_new, alpha))
    # Compute new gradient
    grad_new = gradient(X_new)
    # Compute beta
    beta = (grad_new @ grad_new) / (grad @ grad)
    # Update search direction
    P = -grad_new + beta * P
    # Update X and gradient for the next iteration
    X, grad = X_new, grad_new

results

九、使用牛顿法求解无约束非线性规划问题

其中， $X=(x_1,x_2)^T$ ，取迭代起始点为 $X_0=(1,2)^T$ 。

代码：

# Define the gradient and Hessian functions
def gradient(X):
    x1, x2 = X
    df_dx1 = 3 * (x1 - x2)**2 + 2 * (x1 + 3 * x2)
    df_dx2 = -3 * (x1 - x2)**2 + 6 * (x1 + 3 * x2)
    return np.array([df_dx1, df_dx2])

def hessian(X):
    x1, x2 = X
    d2f_dx1dx1 = 6 * (x1 - x2) + 2
    d2f_dx1dx2 = -6 * (x1 - x2) + 6
    d2f_dx2dx2 = 6 * (x1 - x2) + 18
    return np.array([[d2f_dx1dx1, d2f_dx1dx2],
                     [d2f_dx1dx2, d2f_dx2dx2]])

# Initial conditions
X = np.array([1.0, 2.0])  # Starting point

# Store results for the first two iterations
results = []

# Perform two iterations of Newton's method
for _ in range(2):
    grad = gradient(X)  # Gradient at X
    H = hessian(X)      # Hessian at X
    H_inv = np.linalg.inv(H)  # Inverse of Hessian
    X_new = X - H_inv @ grad  # Newton update
    results.append(X_new)  # Store the updated X
    X = X_new  # Update X for the next iteration

results

十、牛顿法存在哪些缺陷？拟牛顿法为何能克服这些缺陷？

Hessian 矩阵计算

需要明确计算

通过梯度近似逐步构造

Hessian 矩阵逆计算

显式计算

通过递推公式逐步更新逆矩阵

计算成本

高，复杂度O(n^3)

较低，复杂度 O(n^2)

稳定性

可能发散（Hessian 非正定）

更稳定，近似矩阵保持正定

适用场景

低维问题或二次优化问题

高维问题，非线性优化

牛顿法的缺陷

需要计算 Hessian 矩阵：
- 牛顿法需要计算目标函数的 Hessian 矩阵（即二阶导数矩阵）。
- 在高维问题中，Hessian 矩阵的计算和存储成本很高（尤其是当维度较高时，Hessian 是一个 $n \times n$ 的矩阵）。
- 若 Hessian 矩阵稀疏性较差，计算代价会进一步增加。
需要计算 Hessian 的逆矩阵：
- 每次迭代中需要求解线性方程组（等价于求 Hessian 矩阵的逆矩阵）。
- Hessian 矩阵逆的计算复杂度为 $O(n^3)$ ，对高维优化问题来说非常昂贵。
Hessian 矩阵可能是非正定的：
- 如果目标函数的 Hessian 矩阵不是正定矩阵，牛顿法可能会走向错误的方向，导致迭代发散。
- 特别是在非凸优化问题中，Hessian 可能有负特征值。
初始点敏感：
- 牛顿法是基于二阶泰勒展开，假设当前点附近的函数曲率能够很好地反映全局行为。
- 如果初始点距离最优解较远，可能会导致牛顿法不收敛甚至发散。

拟牛顿法如何克服牛顿法的缺陷

拟牛顿法（Quasi-Newton Method）通过近似 Hessian 矩阵及其逆矩阵，克服了牛顿法的上述缺陷。其主要思想是逐步构造一个对 Hessian 的近似，而不直接计算 Hessian。

核心优点

避免显式计算 Hessian 矩阵：
- 拟牛顿法通过梯度信息来逐步更新一个 Hessian 的近似矩阵。
- 避免了昂贵的 Hessian 矩阵计算，尤其在高维优化问题中显得更加高效。
避免直接求 Hessian 的逆矩阵：
- 拟牛顿法使用更新公式构造 Hessian 近似的逆矩阵（如 BFGS 方法）。
- 在每次迭代中，仅通过向量运算更新近似矩阵，计算成本大大降低。
更好的数值稳定性：
- 拟牛顿法使用的近似 Hessian 通常能保持正定性，从而避免了非正定 Hessian 导致的问题。
- 例如，BFGS 算法通过修正保证近似矩阵始终正定。
对初始点鲁棒性更强：相较于牛顿法，拟牛顿法对初始点的依赖性更低，即使远离最优解，仍能逐步收敛。

常见拟牛顿方法

DFP 方法（Davidon–Fletcher–Powell）：
- 最早的拟牛顿方法，通过逐步更新 Hessian 矩阵的逆。
BFGS 方法（Broyden–Fletcher–Goldfarb–Shanno）：
- 最常用的拟牛顿方法，直接更新 Hessian 矩阵逆的近似。
- 保证更新的近似矩阵始终对称且正定。
L-BFGS 方法（Limited-memory BFGS）：
- BFGS 方法的变种，适用于高维问题。
- 不存储完整的 Hessian 矩阵，只存储最近几次迭代的信息。

十一、使用拟牛顿法求解无约束非线性规划问题

$\min f(X) = (4 - x_2)^3 + (x_1 + 4x_2)^2$
其中， $X = (x_1, x_2)^T$ ，取迭代起始点为 $X^0 = (2, 1)^T$ 。

代码：

# Define the gradient function
def gradient(X):
    x1, x2 = X
    df_dx1 = 2 * (x1 + 4 * x2)
    df_dx2 = -3 * (4 - x2)**2 + 8 * (x1 + 4 * x2)
    return np.array([df_dx1, df_dx2])

# Initialize parameters
X = np.array([2.0, 1.0])  # Starting point
B = np.eye(2)  # Initial Hessian approximation (identity matrix)

# Store results for the first two iterations
results = []

# Perform two iterations of quasi-Newton method (BFGS update)
for _ in range(2):
    grad = gradient(X)  # Gradient at current X
    # Compute the search direction
    P = -np.linalg.inv(B) @ grad
    # Update X
    X_new = X + P
    # Store the result
    results.append(X_new)
    # Compute new gradient
    grad_new = gradient(X_new)
    # Update B using the BFGS formula
    s = X_new - X
    y = grad_new - grad
    B = B + np.outer(y, y) / (y.T @ s) - (B @ np.outer(s, s) @ B) / (s.T @ B @ s)
    # Update X for the next iteration
    X = X_new

results

十二、证明：当损失函数是对数损失函数时，经验风险最小化等价于极大似然估计。

十三、与梯度下降方法相比，随机梯度方法为何能降低算法的时间复杂度？

方法	每次梯度计算复杂度	适用场景
梯度下降法 (GD)	O(n)	小规模数据，追求高精度
随机梯度下降法 (SGD)	O(1)	大规模数据，在线学习，训练时间较短需求

梯度下降法（GD, Gradient Descent）

原理：每次迭代计算整个训练集上的梯度（全局梯度）来更新模型参数。
计算公式：

其中：
计算特点：
- 每次梯度计算需要遍历整个训练集，时间复杂度为 O(n)，其中 n 是样本数量。
- 对于大规模数据集（如数百万或更多样本），计算代价非常高。

随机梯度下降法（SGD, Stochastic Gradient Descent）

原理：每次迭代随机抽取一个样本计算梯度，用该样本的梯度近似全局梯度，更新模型参数。
计算公式：

其中：
- $x_i, y_i$ 是随机抽取的一个样本。
- $\nabla \ell(y_i, f(x_i; \theta))$ 是该样本的梯度。
计算特点：
- 每次迭代仅需计算单个样本的梯度，时间复杂度为 O(1)。
- 随着训练的进行，随机梯度下降在总体上会接近全局最优解。

随机梯度下降法如何降低时间复杂度

每次梯度计算更快：
- 梯度下降法需要对整个数据集计算平均梯度，计算复杂度为 O(n)。
- 随机梯度下降法只需单个样本的梯度，计算复杂度为 O(1)。
迭代次数的折中：
- 虽然随机梯度下降的收敛速度可能比梯度下降稍慢（波动性较大），但每次迭代的时间开销远低于梯度下降法。
- 对于大规模数据集，随机梯度下降在整体运行时间上仍然显著优于梯度下降。
适合在线学习：在实时或动态数据环境中，随机梯度下降可以直接更新模型，而不需要等到所有数据都准备好后再计算全局梯度。
可实现更高频率的更新：随机梯度下降方法的快速更新使其可以更频繁地调整模型参数，从而在许多实践场景中能更快地获得性能提升。

十四、小批量随机梯度下降法与随机梯度下降法有何区别？这样设计小批量随机梯度下降法的原因是什么？

每次迭代样本量

单个样本

小批量样本

计算复杂度

每次更新计算快，复杂度低

较 SGD 高，但低于全梯度下降

梯度波动性

较大，容易不稳定

较小，更接近全局梯度

收敛速度

较慢，收敛过程不平稳

更快，收敛稳定性更强

硬件利用

计算无法并行化，效率低

利用并行计算能力，效率高

适用场景

超大规模数据

中大规模数据，适配并行硬件

小批量随机梯度下降法（Mini-batch SGD）

原理：每次迭代时，从训练数据中随机抽取一个小批量（mini-batch）样本，基于该批量的平均梯度更新模型参数。
公式：其中 m 是小批量的样本数。
特点：
- 优点：
  - 梯度波动性小于 SGD，提高了收敛的稳定性。
  - 通过小批量数据计算，可以更好地利用硬件（如 GPU）的并行能力，加速梯度计算。
- 缺点：相比 SGD，每次更新的计算量略大。

随机梯度下降法（SGD）

原理：每次迭代时，从训练数据中随机抽取一个样本，基于该样本计算梯度，更新模型参数。
- 公式：
- 其中 $(x_i, y_i)$ 是一个随机样本。
特点：
- 优点：计算量小，每次只处理一个样本，适合大规模数据集。
- 缺点：梯度计算波动较大，可能导致收敛过程不稳定；无法充分利用硬件的并行计算能力。

十五、证明

设 $P(Y \mid \theta)$ 为观测数据的似然函数， $\theta^{(i)} (i=1,2,\cdots)$ 为用 EM 算法得到的参数估计序列， $P(Y \mid \theta^{(i)}) (i=1,2,\cdots)$ 为对应的似然函数序列，则 $P(Y \mid \theta^{(i)})$ 是单调递增的。

1. 定义辅助函数 $Q(\theta \mid \theta^{(i)})$

在第 i 次迭代中，辅助函数 $Q(\theta \mid\theta^{(i)})$ 表示条件期望：

$Q(\theta \mid \theta^{(i)}) = \int P(Z \mid Y, \theta^{(i)}) \ln P(Y, Z \mid \theta) \, dZ$

2. 似然函数的关系

根据 Jensen 不等式，可以证明对数似然函数有以下关系：

$\ln P(Y \mid \theta) \geq Q(\theta \mid \theta^{(i)})$

3. E 步和 M 步的单调性

E 步：不改变似然值，仅计算 $Q(\theta \mid \theta^{(i)})$ 。
M 步：更新参数
因此： $Q(\theta^{(i+1)} \mid \theta^{(i)}) \geq Q(\theta^{(i)} \mid \theta^{(i)})$

4. 似然函数的单调性

由 EM 算法性质：

$Q(\theta^{(i+1)} \mid \theta^{(i)}) \geq Q(\theta^{(i)} \mid \theta^{(i)})$

结合 Jensen 不等式，得到：

$\ln P(Y \mid \theta^{(i+1)}) \geq \ln P(Y \mid \theta^{(i)})$

结论

通过以上分析，EM 算法在每次迭代中都保证：

$P(Y \mid \theta^{(i+1)}) \geq P(Y \mid \theta^{(i)})$

即似然函数 $P(Y \mid \theta^{(i)})$ 是单调递增的。

简单来说：

在 EM 算法中，E 步不改变似然值，只是计算期望；
在 M 步中，通过最大化辅助函数 Q，保证似然值 P(Y∣θ)增大；
因此，EM 算法的似然函数 P(Y∣θ) 在每次迭代后都不会减少。

十六、蒙特卡洛方法的理论基础是什么？如何使用蒙特卡洛方法估计圆周率的取值？马可夫链蒙特卡洛方法有哪些具体应用？

简单讲一下：

蒙特卡洛方法的基础是随机采样和大数法则，用于近似期望值、积分或分布。
估算圆周率通过统计随机点落在圆内的比例，利用几何关系得出结果。
MCMC 方法结合了马尔可夫链和蒙特卡洛采样，能够高效处理复杂分布的采样问题，在贝叶斯统计、机器学习和物理模拟中有广泛应用。

蒙特卡洛法核心思想

蒙特卡洛方法是一种基于随机采样的数值计算方法，其理论基础是大数法则和概率统计理论：

大数法则：
- 大数法则表明，当随机变量的独立样本数足够大时，其样本均值会收敛于总体期望值。
- 如果随机变量 X 的期望为 E[X]，通过多次采样 $X_1, X_2, \dots, X_n$ ，可以近似计算： $\mathbb{E}[X] \approx \frac{1}{n} \sum_{i=1}^n X_i$
概率理论：
- 蒙特卡洛方法利用随机采样的分布来近似复杂的概率分布或积分。
- 通过构造采样过程和统计样本的性质，可以求解高维积分、期望或概率等问题。

使用蒙特卡洛方法估计圆周率

原理

假设在单位正方形内（边长为 2，中心为原点）绘制一个单位圆（半径为 1），则：

单位圆面积占正方形面积的比例为 $\frac{\pi}{4}$ 。
通过随机生成点在正方形内的位置，统计这些点落在圆内的比例，可以近似估算 π。

步骤

随机点生成：在区间 $[-1, 1] \times [-1, 1]$ 中均匀随机生成 n 个点 (x,y)。
判断点是否落入圆内：若 $x^2 + y^2 \leq 1$ ，则点落在单位圆内。
计算比例：记落在圆内的点数为 k，则：
估计圆周率：根据上述公式，圆周率估计值为：

马尔可夫链蒙特卡洛方法（MCMC）及其应用

MCMC 方法的定义

马尔可夫链：一种随机过程，其中当前状态只依赖于前一个状态，与更早的历史无关。
MCMC 方法：结合马尔可夫链和蒙特卡洛方法，利用马尔可夫链的平稳分布性质，从复杂概率分布中进行采样，进而近似计算概率分布的期望值或其他统计量。

MCMC 的步骤

构造一个马尔可夫链，使其平稳分布为目标概率分布 p(x)。
从马尔可夫链中采样，得到依赖于 p(x) 的样本。
使用这些样本进行蒙特卡洛估计。

MCMC 的应用

贝叶斯推断：
- 在贝叶斯统计中，后验分布通常难以显式计算。
- MC 方法（如 Metropolis-Hastings 和 Gibbs 采样）可用于从后验分布中采样，近似计算期望值、概率或边际分布。
高维积分：MCMC 方法可用于求解高维积分问题，例如在物理模拟中计算系统的期望能量或分配函数。
机器学习中的应用：
- 生成对抗网络（GAN）：MCMC 方法用于生成样本。
- 隐马尔可夫模型（HMM）：通过 MCMC 方法推断隐藏状态。
图像处理：MCMC 用于图像去噪、分割或修复问题，特别是在需要随机模拟的情境中。
物理模拟：MCMC 在统计物理中用于模拟高维复杂系统，如模拟材料的分子动力学行为。

十七、模型的正则化方法有哪些？它们分别是从什么角度出发对模型进行正则化的？

正则化方法总结

正则化方法	核心思想	应用场景
L1正则化	限制特征的绝对值，产生稀疏解	特征选择、高维数据
L2 正则化	限制特征的平方和，防止权重过大	回归模型、高维数据、神经网络
Dropout	随机屏蔽神经元，减少过拟合	深度学习、全连接层
数据增强	增加数据多样性，扩展训练集规模	图像、文本、时序数据
Early Stopping	限制训练轮次，避免训练过长导致过拟合	神经网络训练

正则化方法从多个角度（损失函数、数据、训练过程）限制模型的复杂性，提升泛化能力。在实际应用中，不同任务通常会组合使用多种正则化方法来取得最优效果。

1. $L_1$ 正则化

定义：在损失函数中加入权重的 $L_1$ 范数（即权重绝对值的和）的惩罚项。

其中：
- $\text{Loss}(\theta)$ ：模型的原损失函数。
- λ：正则化强度的超参数。
- $|\theta_j|$ ：权重的绝对值。
核心思想：通过惩罚权重的绝对值，鼓励模型将部分不重要的特征权重变为零，达到特征选择的效果。
应用场景：
- 特征稀疏化，例如 Lasso 回归。
- 在数据维度较高的情况下（如文本数据），有效去除无关特征。

2. $L_2$ 正则化

定义：在损失函数中加入权重的 $L_2$ 范数（即权重平方和）的惩罚项。
核心思想：通过惩罚权重的平方，限制模型权重的大小，防止权重过大导致模型过拟合。
特点：
- 与 $L_1$ 不同， $L_2$ 正则化不会将权重变为完全的零，而是会使权重趋近于零（缩小权重值）。
- 提升模型的平滑性，适合多项式回归等高维度问题。
应用场景：
- Ridge 回归（岭回归）。
- 广泛应用于神经网络训练中，防止模型过拟合。

3. Dropout

定义：在每次训练迭代时，随机“丢弃”一定比例的神经元（即设置为零）。
- Dropout 的公式体现在训练中，并没有显式的数学表达式。
- 在预测阶段，所有神经元均参与运算，但权重按训练时的保留率缩放。
核心思想：通过随机屏蔽神经元，减弱神经元之间的协同适应性，使模型更鲁棒。
特点：
- 相当于在训练时构造多个不同的子网络并对其进行训练。
- 防止神经网络中的神经元过拟合到训练数据。
应用场景：
- 深度神经网络（特别是全连接层）。
- 图像分类、自然语言处理等领域的模型训练。

4. 数据增强（Data Augmentation）

定义：通过对训练数据进行各种合理的变换（如旋转、平移、翻转等），扩展数据集的规模。
- 不直接对损失函数添加惩罚，而是从数据层面增加数据多样性。
核心思想：通过增加数据样本的多样性，让模型在不同的样本上学习，减少过拟合风险。
应用场景：
- 图像分类（如随机翻转、裁剪、亮度调整等）。
- 自然语言处理（如同义词替换、随机删除等）。
- 时序数据（如时间窗口扩展）。

5. Early Stopping（早停法）

定义：在训练过程中，实时监控验证集上的损失，当损失不再下降（甚至上升）时，停止训练。
核心思想：通过限制训练轮次，防止模型在训练集上过度拟合。
特点：
- 不需要修改损失函数，也无需添加额外的惩罚项。
- 与验证集的表现高度相关。
应用场景：
- 深度学习模型（如神经网络）。
- 在训练时间较长的任务中，常配合 Dropout 等方法使用。

6. 正则化的贝叶斯视角

从贝叶斯统计的角度看，正则化可以视为对模型参数的先验约束：
- L1 正则化对应于拉普拉斯分布的先验假设。
- L2正则化对应于高斯分布的先验假设。

通过引入先验信息，正则化方法让模型更偏向简单解，避免过拟合。

十八、在范数惩罚正则化中

使用 $L^2$ 范数惩罚可以达到什么样的约束效果？使用 $L^1$ 范数惩罚又能达到什么样的约束效果？能够达到这些约束效果的原因是什么？

特性	L2 正则化（Ridge）	L1 正则化（Lasso）
惩罚方式	参数平方和	参数绝对值和
对权重的影响	所有权重趋于接近零，但不完全为零	部分权重直接为零，导致稀疏性
特征选择能力	不具有特征选择能力	具有特征选择能力
适用场景	数据维度不高，特征重要性较为均衡的场景	高维稀疏数据，部分特征重要性较高的场景

L2 正则化通过限制权重大小，提升模型的平滑性，防止过拟合，但不会完全去除特征。
L1 正则化通过惩罚绝对值实现稀疏解，适合特征选择和高维稀疏数据场景。
两者的约束效果与数学形式相关，L1 的“稀疏性”来源于梯度在零点处的不连续性，而 L2 则通过均匀惩罚限制权重整体大小。

L2约束效果

缩小参数值：
- L2正则化通过惩罚参数的平方，使得权重值尽可能小，接近于零，但通常不完全为零。
- 因此，它不会完全删除特征，而是倾向于保留所有特征，只是将不重要特征的权重缩小。
提升模型的平滑性：L2 正则化通过限制参数的大小，使得模型更加平滑，降低模型对噪声的敏感性，减小过拟合风险。
抗多重共线性：特别是在多项式回归或高维数据中，L2正则化可以减少不同特征之间的相互依赖，缓解多重共线性问题。

原因

L2正则化的平方和约束会对所有参数施加均匀的惩罚，限制了参数的整体大小。
数学上，L2正则化增加了目标函数的凸性，使得优化更加稳定，并倾向于寻找更小权重的解。

L1约束效果

稀疏解：
- L1正则化会将部分参数的值直接压缩到零，从而完全去除这些参数对应的特征。
- 因此，L1正则化具有特征选择的效果，适合处理高维稀疏数据。
提升模型的可解释性：由于很多参数被置为零，模型仅依赖少量的特征进行预测，使得模型更加简单、直观。
减少过拟合：通过去除不重要的特征，L1正则化降低了模型的复杂性，从而提高泛化能力。

原因

L1范数的绝对值形式导致梯度不连续，当权重接近零时，梯度变化较大，容易直接将权重压缩为零。
这种特性让 L1正则化在特征选择中表现优异，但在优化过程中可能不如 L2正则化平滑。

十九、试求将该图像顺时针旋转 $\theta$ 度后该像素点所对应的新的坐标。

对于图像 $X$ ，假设在以图像中心点为原点建立的坐标系中，某个像素点的坐标为 $(x, y)$

import numpy as np

def rotate_point(x, y, width, height, theta_degrees):
    """
    Rotate a point (x, y) around the center of an image with dimensions (width, height)
    by an angle theta (in degrees).

    Args:
        x (float): Original x-coordinate of the point.
        y (float): Original y-coordinate of the point.
        width (int): Width of the image.
        height (int): Height of the image.
        theta_degrees (float): Rotation angle in degrees (clockwise).

    Returns:
        (float, float): New coordinates of the point after rotation.
    """
    # Convert angle from degrees to radians
    theta = np.radians(theta_degrees)
    
    # Translate point to the center of the image (centered coordinates)
    x_c = x - width / 2
    y_c = y - height / 2

    # Apply rotation matrix
    x_c_rotated = x_c * np.cos(theta) + y_c * np.sin(theta)
    y_c_rotated = -x_c * np.sin(theta) + y_c * np.cos(theta)

    # Translate point back to the original coordinate system
    x_rotated = x_c_rotated + width / 2
    y_rotated = y_c_rotated + height / 2

    return x_rotated, y_rotated

# Example usage
width, height = 200, 100  # Image dimensions (width, height)
x, y = 150, 50            # Original point coordinates
theta_degrees = 45        # Rotation angle in degrees (clockwise)

rotated_x, rotated_y = rotate_point(x, y, width, height, theta_degrees)
(rotated_x, rotated_y)

得到旋转后的点坐标为 $(135.36,14.64)$ 。

二十、对抗样本的存在会对机器学习模型造成怎样的危害？对抗训练方法为何能提升模型的鲁棒性？

对抗样本的危害

降低模型预测准确性；
威胁模型在关键场景中的安全性；
揭示模型对输入扰动的脆弱性；
降低用户对模型的信任。

对抗训练的效果

提升模型在复杂场景下的鲁棒性；
减少对特定输入分布的过拟合；
优化模型的损失表面，增强对输入扰动的抵抗能力；
增强模型对潜在攻击的防御能力。

1. 降低模型的预测准确性

对抗样本通过扰动原始数据，使得模型的输出结果产生重大偏差，从而大幅降低模型在对抗样本上的性能。
在图像分类任务中，比如一个“猫”的图像加上对抗扰动后，模型可能错误地预测为“狗”或“汽车”。

2. 威胁模型的安全性

在实际应用中，对抗样本可能被恶意利用，导致安全隐患：
- 自动驾驶：摄像头中的交通标志通过对抗扰动被错误识别为错误的标志（如“限速”识别为“转向”）。
- 人脸识别：通过添加微小扰动，恶意攻击者可以使模型将其识别为其他人，从而绕过安全系统。
- 金融欺诈：对抗扰动可以导致信用评分或欺诈检测系统做出错误判断。

3. 暴露模型的脆弱性

对抗样本的存在揭示了深度学习模型的弱点：
- 模型在输入分布的微小变化下表现出极大的敏感性，说明模型并未真正学到数据的本质特征，而是对输入数据的特定模式进行了过拟合。
- 这种现象表明模型的泛化能力较差，容易受到未见数据分布的干扰。

4. 降低用户信任

对抗样本让用户对模型的可靠性产生质疑，特别是在关键任务（如医疗诊断、自动驾驶）中，模型的错误预测可能导致严重后果。

对抗训练如何提升模型的鲁棒性

1. 什么是对抗训练？

对抗训练（Adversarial Training）是一种提升模型鲁棒性的训练方法：

在训练过程中，生成对抗样本，并将这些对抗样本加入训练数据中，使得模型在这些样本上也能表现良好。
损失函数被修改为同时最小化原始样本和对抗样本的误差。

2. 对抗训练提升鲁棒性的原因

增强了模型的泛化能力
- 对抗训练通过引入对抗样本，让模型学会在更加复杂和多样的输入分布上做出正确预测。
- 模型学习到了对抗扰动的方向，减少了对这种特定扰动的敏感性，从而提升了鲁棒性。
减少模型的过拟合：对抗样本引入了不同于原始样本分布的干扰，使得模型必须在更广泛的分布上学习特征，而不是对训练数据过拟合。
优化了模型的损失表面
- 对抗训练改变了模型的损失函数表面，使得模型的预测在输入的小扰动下更加稳定。
- 通过对抗训练，模型参数的更新方向更倾向于提升整体鲁棒性，而不仅仅优化训练数据上的性能。
提升模型的安全性：通过对抗训练，模型能够有效识别并抵抗攻击者生成的对抗样本，从而降低对抗攻击的成功率。