常见递归的解题思路

引言：递归是一种强大的编程技术，通过将一个问题分解为更小的相同类型问题来解决复杂的任务。它不仅可以使代码更简洁明了，还能够有效地处理多层次的结构。在许多经典问题中，递归都扮演着重要的角色，我们可以探索递归问题的常见思路，了解何时适用于递归、如何编写递归代码，以及如何结构化和实现递归过程。
接下来我会以经典递归问题汉诺塔为例，来展示递归问题的常规思路

1.什么情况下可以用递归

想要用递归需要满足以下两种条件：

• 可以将大问题转换为相同类型子问题；
• 可以将子问题转换成相同类型子问题

由于盘子只能小的放大的上面，所以要想将a上所有的盘子放在c上，那么最大的盘子（即第n个盘子）必须放在c上；而要想将最大的盘子放在c上，需要将该盘子上面的所有盘子挪开，即将a上n-1个盘子放在b上；

而为了将a上n-1个盘子放在b上，则需要将a上最大的盘子（此时为第n-1个盘子）必须先放在b上；要想将最大的盘子放在b上，需要将该盘子上面所有的盘子挪开，即将a上n-2个盘子放在c上

…

以此不断递归，从中可以看出大问题是：将a上n个盘子放在c上；可以分为相同子问题：将a上n-1个盘子放在b上；而这子问题又可以按照此方法不断细分，所有此题可以用递归解决。

2.如何编写递归代码

解决递归问题常用以下三个步骤：

• 重复子问题->函数头
• 只关心一个子问题怎么实现->函数体
• 问题不能再细分->递归的出口

接下来以汉诺塔问题为例来进行解析

2.1.重复子问题->函数头

通过重复子问题所需要的元素来确定函数头。

重复的子问题是：将x柱子上的n个盘子通过y柱子，转到c柱子上。

• 其中所需要的元素是x，y，z三个柱子，和盘子的个数n；
• 在本题中柱子是由列表来表示的，盘子是由整数型来表示的；
• 所以函数需要3个列表x，y，z，一个整型n。

我们定义递归函数名为dfs，由此可得函数头为：

这个函数的作用就是将a柱子的n个盘子转移到c柱子上。

2.2.子问题的实现->函数体

我们只关心一个子问题是怎么实现的，然后提前子问题实现的步骤来确定函数体

本问题只有三步：

• 1.将a柱子上的n-1个盘子转移到b上，此时a上只剩1个盘子；
• 2.将a上的最后一个盘子转移到c上；
• 3.将b上的n-1个盘子转移到c上。

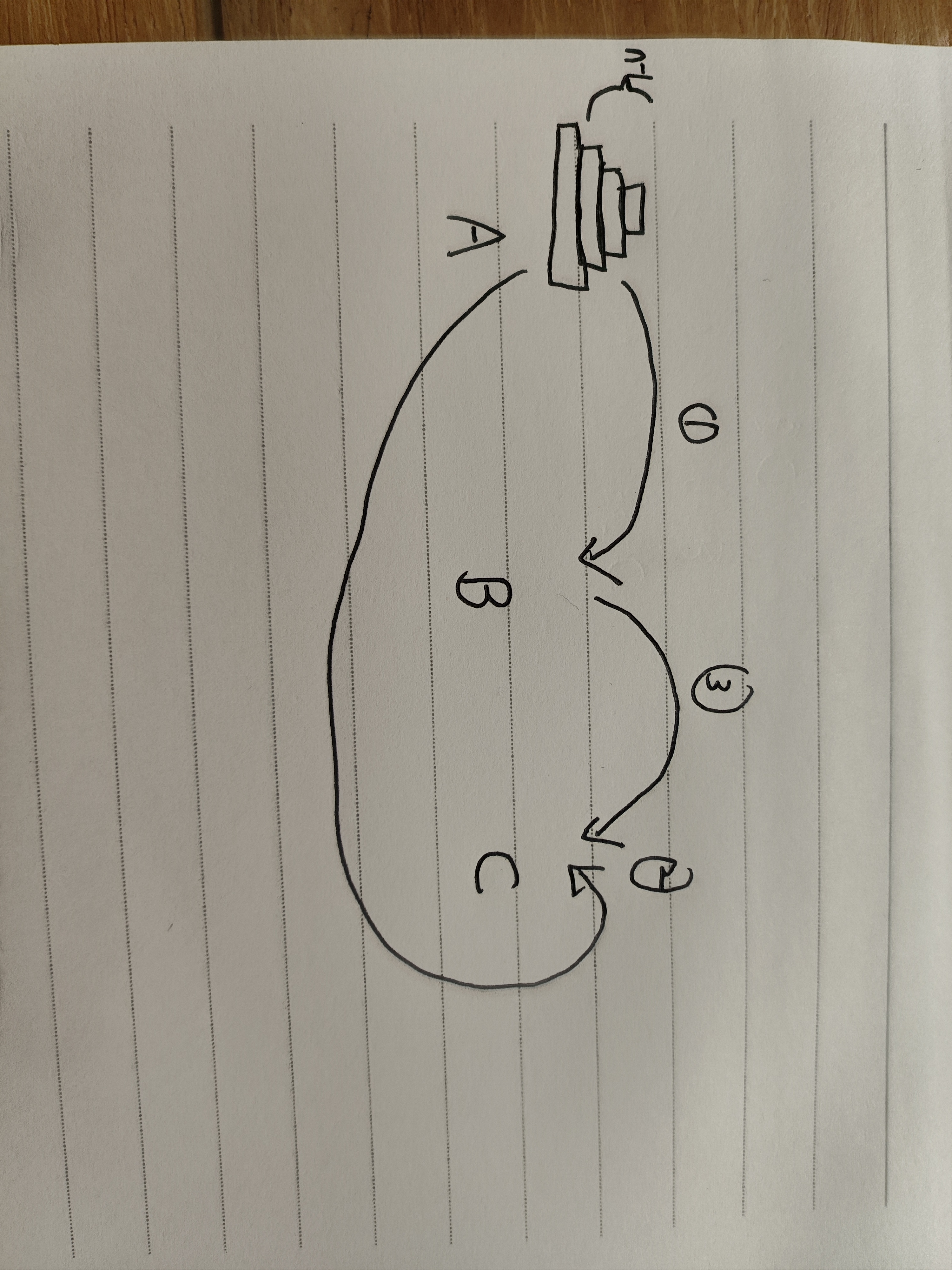
第一步转化为代码： dfs(a,c,b,n-1);

第二步转化为代码： c.add(a.remove(a.size()-1));

第三步转化为代码： dfs(b,a,c,n-1);

2.3.问题不能再细分->递归的出口

当问题不能再细分的时候，最后一个子问题就是递归的出口。

本题中当n的数量为1的时候，就不能再分成新的子问题，而是直接将a上的盘子转移到c上，所以n=1时就是递归的出口

代码为：

if(n==1){
            c.add(a.remove(a.size()-1));
            return;
        }

总代码

class Solution {
    public void hanota(List<Integer> a, List<Integer> b, List<Integer> c) {
        dfs(a,b,c,a.size());
    }

    public void dfs(List<Integer> a, List<Integer> b, List<Integer> c,int n){
        //递归出口
        if(n==1){
            c.add(a.remove(a.size()-1));
            return;
        }
        //递归函数体
        dfs(a,c,b,n-1);
        c.add(a.remove(a.size()-1));
        dfs(b,a,c,n-1);
    }
}

题目链接

面试题 08.06. 汉诺塔问题 - 力扣（LeetCode）