LeetCode螺旋矩阵II&&将所有数字用字符替换

目录

一.螺旋矩阵

题目描述：

代码实现： 

解题思路： 

二.将所有数字用字符替换 

题目描述：

代码实现：

解题思路：

---

一.螺旋矩阵

题目描述：

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

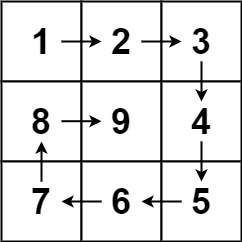
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

输入：n = 1
输出：[[1]]

提示：

• 1 <= n <= 20

代码实现： 

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
int** generateMatrix(int n, int* returnSize, int** returnColumnSizes) {
    * returnColumnSizes=(int *)malloc(sizeof(int)*n);
    * returnSize=n;
    int **arr=(int **)malloc(sizeof(int*)*n);
    for(int k=0;k<n;k++)
    {
        arr[k]=(int *)malloc(sizeof(int)*n);
        (* returnColumnSizes)[k]=n;
    }
    int i=0,j=0,startx=0,starty=0,x,y,t=1;
    int count=1;
        x=n/2;
    while(x)
    {
        int i=startx;
        int j=starty;
        for(;j<n-t;j++)
        {
            arr[i][j]=count;
            count++;
        }
        for(;i<n-t;i++)
        {
            arr[i][j]=count;
            count++;
        }
        for(;j>starty;j--)
        {
            arr[i][j]=count;
            count++;
        }
        for(;i>startx;i--)
        {
            arr[i][j]=count;
            count++;
        }
        t++;
        x--;
        startx++;
        starty++;
    }
    if(n%2!=0)
    {
        arr[n/2][n/2]=count;
    }
    return arr;
}

解题思路： 

       首先为将要返回的矩阵分配内存空间，*returnColumnSize返回生成矩阵每一列的大小，为每一行数组申请空间，在循环中为每一列数组申请空间并赋值每一列的元素数目。

      其次思考在螺旋矩阵的实现过程中每次循环的条件（也就是寻找规律，找出每一圈循环过程中的不变量），可以思考出每一圈的四个方向的赋值过程中，每个方向的元素数目都应该相同

     还有我们应确定当前矩阵的循环圈数，偶数和奇数的循环圈数都是矩阵维度整除以2，但奇数与偶数不同的是奇数最中间的最后一个数需要在循环结束后单独输入。

二.将所有数字用字符替换 

题目描述：

给你一个下标从 0 开始的字符串 s ，它的 偶数 下标处为小写英文字母，奇数 下标处为数字。

定义一个函数 shift(c, x) ，其中 c 是一个字符且 x 是一个数字，函数返回字母表中 c 后面第 x 个字符。

• 比方说，shift('a', 5) = 'f' 和 shift('x', 0) = 'x' 。

对于每个 奇数 下标 i ，你需要将数字 s[i] 用 shift(s[i-1], s[i]) 替换。

请你替换所有数字以后，将字符串 s 返回。题目 保证 shift(s[i-1], s[i]) 不会超过 'z' 。

示例 1：

输入：s = "a1c1e1"
输出："abcdef"
解释：数字被替换结果如下：
- s[1] -> shift('a',1) = 'b'
- s[3] -> shift('c',1) = 'd'
- s[5] -> shift('e',1) = 'f'

示例 2：

输入：s = "a1b2c3d4e"
输出："abbdcfdhe"
解释：数字被替换结果如下：
- s[1] -> shift('a',1) = 'b'
- s[3] -> shift('b',2) = 'd'
- s[5] -> shift('c',3) = 'f'
- s[7] -> shift('d',4) = 'h'

提示：

• 1 <= s.length <= 100
• s 只包含小写英文字母和数字。
• 对所有 奇数 下标处的 i ，满足 shift(s[i-1], s[i]) <= 'z' 。

代码实现：

char* replaceDigits(char* s) {
    int len=strlen(s);
    for(int i=0;i<len;i++)
    {
        if(i%2!=0)
        {
            s[i]=s[i-1] + (s[i] - '0');
        }
    }
    return s;
}

解题思路：

首先求出字符串的长度len,得到循环的终止条件，在循环中，判断当前字符下标是否为奇数，若为奇数则将上一个字符加上当前字符的值重新赋值给当前字符的位置。