线性代数：行列式（1）

行列式基础

1.二阶行列式计算

2.三阶行列式计算

三阶行列式为什么是这样得到的呢？

式子一：

式子二：

简单来说：三阶行列式对角线法则就是用主对角线的乘积 减掉 副对角线的乘积

3.如何判断某一项的正负

例题1：

判断4阶行列式中，项a11a23a32a44前面符号的正负

解：（先看脚标，从行和列分别看，行（行指的是每个字母后面第一位数）是1234，列（列指的是每位数字后面第二位数字）是1324）

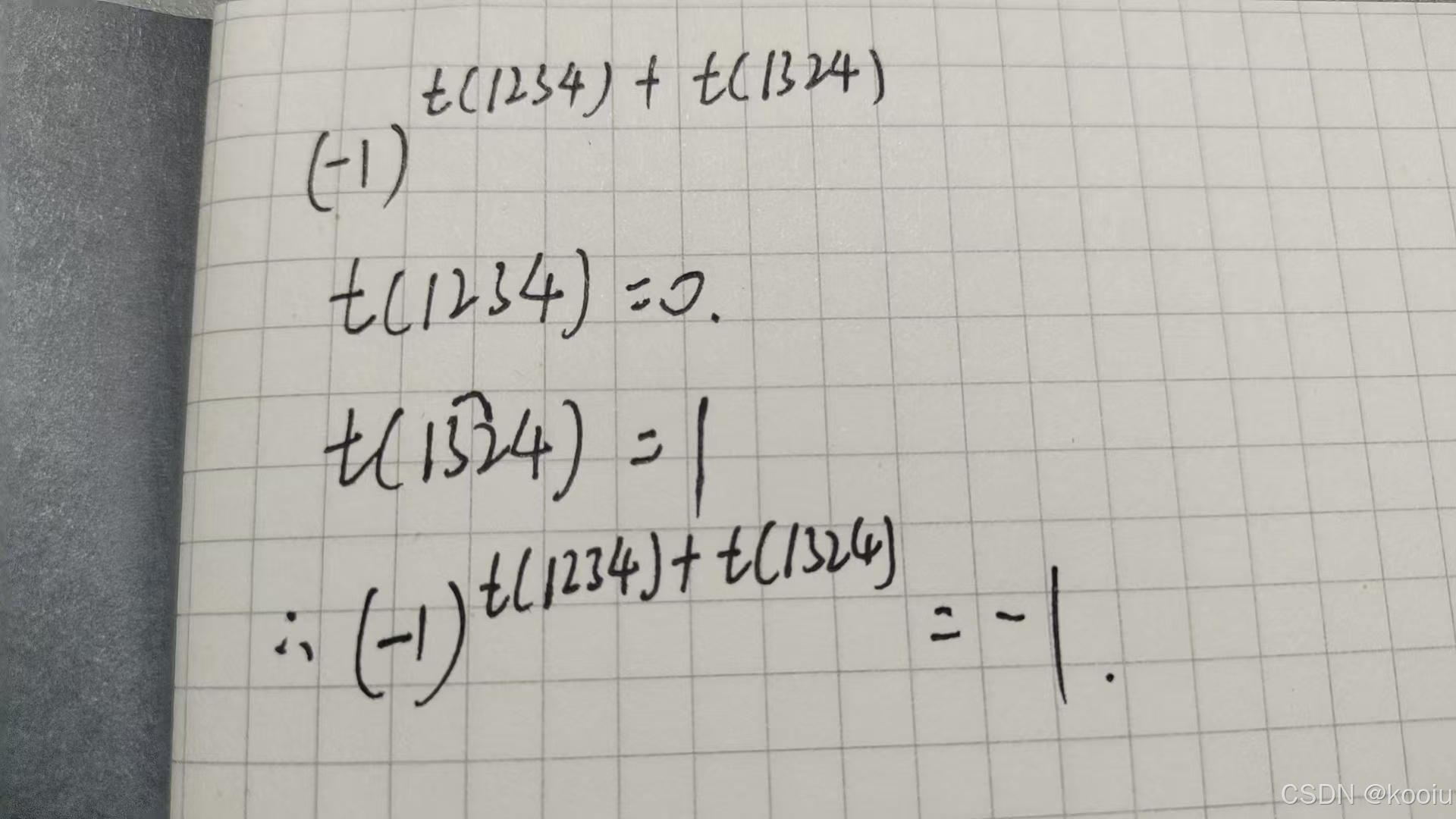
图中的 t() 代表逆序数量，”1234“都是顺序，"1324"中只有32是逆序，所以为1。

因此a11a23a32a44前面为负号。

例题2：

判断4阶行列式中，项a14a23a41a32前面符号的正负

解：（先看脚标，从行和列分别看，行（行指的是每个字母后面第一位数）是1243，列（列指的是每位数字后面第二位数字）是4312）

4.计算行列式

例题1：

解：

思路：从右上往左下选一个不为0的数字（因为0没有意义），选好后划掉该数字的行和列，以此类推。

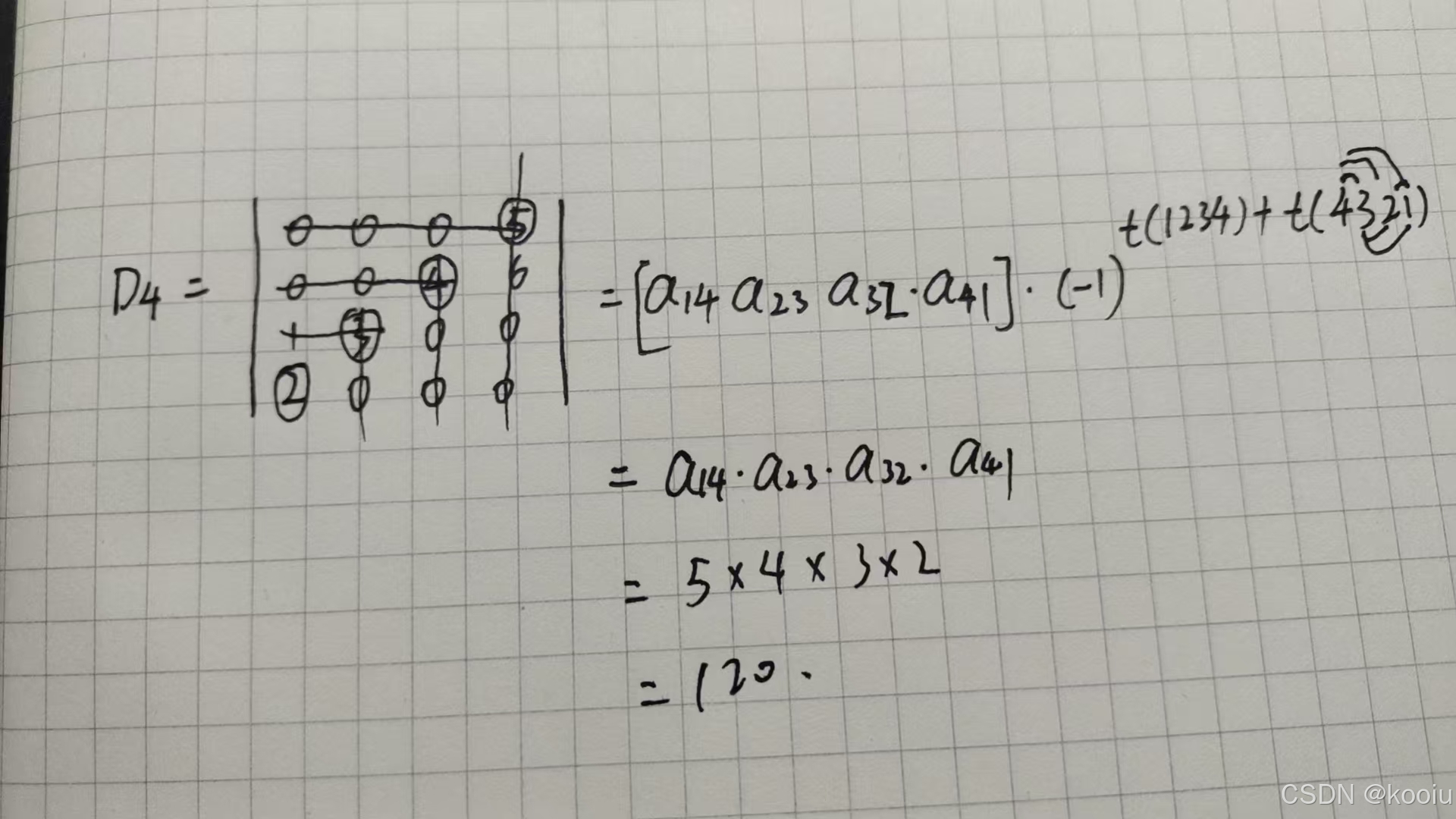
行列式的性质：

性质一

行列式转置，行列式的值不变

转置：每一行变成每一列

性质二

行列式交换两行（列），其值反号

结果相反

推论：

若行列式在两行(列)相同，其值为0

证明：设行列式为D1，交换相同的两行后为D2，则D1 = -D2

又因为 D1 = D2 （因为是相同两行交换）

所以    D1 = -D2 = -D1    

所以   D1 = 0； 

性质三

行列式某行（列）乘k，等价于k乘原行列式

推论：

行列式有两行（列）成比例，其值为0

证明：把比例系数提出来后，两行就相等了，就可以用到性质二中的推论，得到结果为0；

性质四

行列式某行（列）元素均为两个数之和，则行列式可以分解为两个行列式之和。

推论：

一次只能拆一行(列），其它必须保持不变

例题：

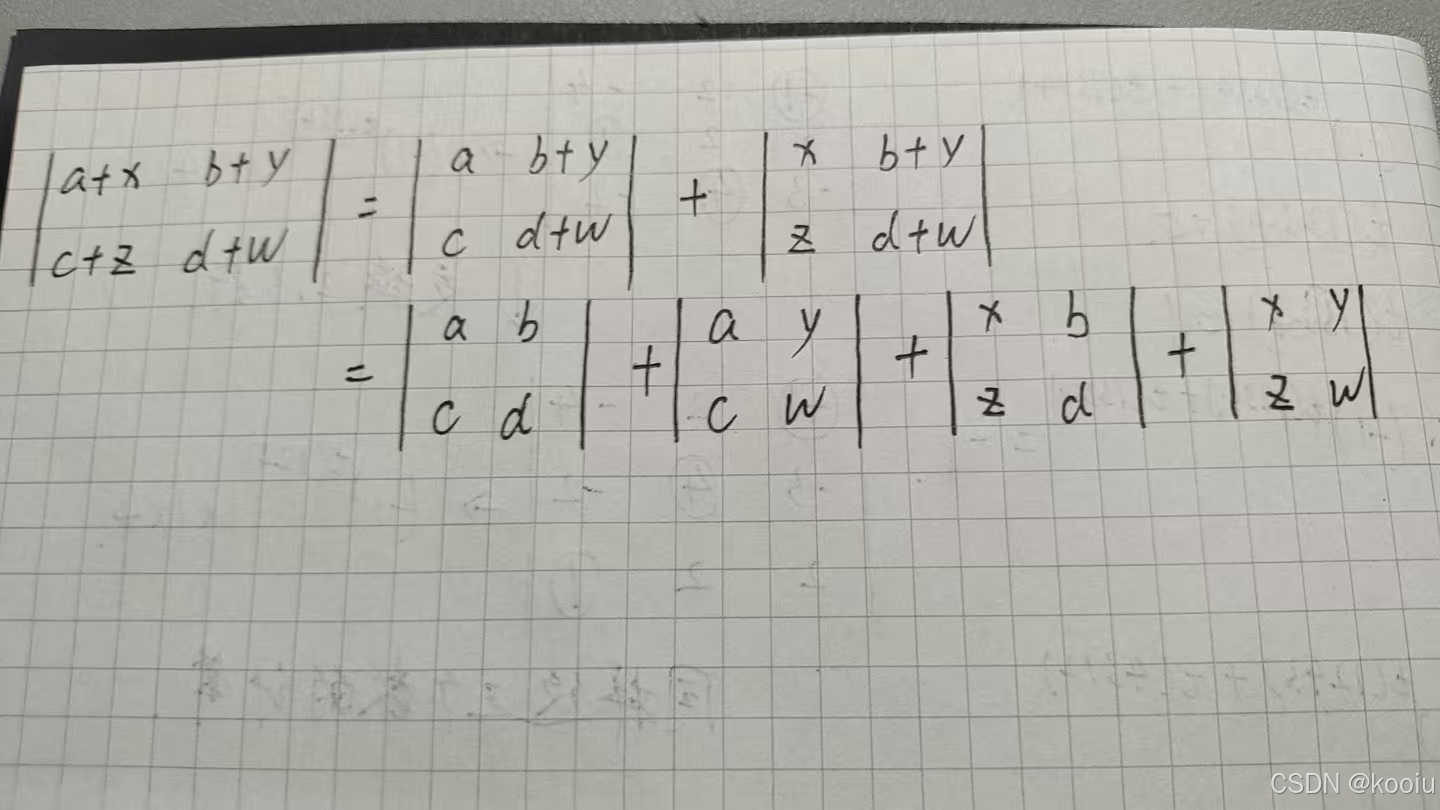
性质五

将行列式的某行（列）的k倍加到另一行(列)上，则行列式的值不变

证明如下：

例题：

四阶行列式计算：

思路.将第一行第一列的元素变为1（或合适的数），然后将主对角线左下角的数都变为0

例题：

总结