2.3.1 线性表的链式存储结构——链表
线性表的链式存储结构称为链表。
线性表的每一个元素用一个内存结点存储,每个结点包括数据域和指针域。数据域用来存储数据,指针域用来指向下一个(或上一个)结点。
指针域设置一个单向指向下一个结点的称为单链表;指针域设置前后两个,指向前驱结点和后继结点的称为双链表。

单链表示意图
空指针:不指向任何结点的指针,用常量NULL表示( ^ 代表空 )

双链表示意图
2.3.2 单链表
链表不具有随机存取的特性 只能顺序存取。
单链表中,增加一个头节点的目的是为了方便运算的实现。
在单链表中,每个结点类型都用LinkNode表示,data的类型用ElemType表示,指针域用next表示
typedef struct LNode
{
ElemType data;
struct LNode *next;
}LinkNode;
LinkNode *L;单链表的基本运算

(1) 初始化线性表InitList(&L):
构造一个空的线性表L。
void InitList(LinkNode *&L)
{
L=(LinkNode *)malloc (sizeof(LinkNode));
L->next=NULL; //创建一个头结点,将其next域置为NULL
}(2) 销毁线性表DestroyList(LinkNode *&L)):
释放线性表L占用的内存空间。
void DestroyList(LinkNode *&L)
{
LinkNode *pre=L,*p=L->next;
while(p!=NULL)
{
free(pre);
pre=p; //pre指向p的前驱结点,遍历单链表L,释放pre结点
p=pre->next; //pre,p同步后移一个结点
}
free(pre); //循环结束时p为NULL,pre指向尾结点并释放
}
(3) 判线性表是否为空表ListEmpty(L):
若L为空表,则返回真,否则返回假。
bool ListEmpty(LinkNode *L)
{
return(L->length==NULL);
}(4) 求线性表的长度ListLength(L):
返回L中元素个数。
int ListLength(LinkNode *L)
{
int n=0;
LinkNode *p=L;
while (p->next !=NULL)
{
n++;
p=p->next;
}
return(n);
} (5) 输出线性表DispList(L)
当线性表L不为空时,顺序显示L中各结点的值域。
void DispList(LinkNode *L)
{
LinkNode *p=L->next;
while(p!=NULL)
{
printf("%d ",L->data);
p=p->next;
}
printf("\n");
}(6) 求线性表L中指定位置的某个数据元素GetElem(L,i,&e)
用e返回L中第i(1≤i≤ListLength(L))个元素的值。
bool GetElem(LinkNode *L,int i,ElemType &e)
{
int j=0;
LinkNode*p=L;
if (i<=0)
{
return false;
}
while(j<i&&p!=NULL)
{
j++;
p=p->next;
}
if (p==NULL)
{
return false;
}
else {
e=p->data;
return true;
}
}(7) 定位查找LocateElem(L,e)
返回L中第1个值域与e相等的位序。若这样的元素不存在,则返回值为0。
int LocateElem(LinkNode *L, ElemType e)
{
int i=1;
LinkNode *p=L->next;
while (p!=NULL&&p->data!=e)
{
p=p->next;
i++;
}
if (p==NULL)
return (0);
else
return (i);
}(8) 插入数据元素ListInsert(&L,i,e)
描述:将值为e的新结点插入到单链表的第i个结点的位置上
操作步骤:
- 找到第i-1个结点*p
- 创建结点*s
- 修改结点*s中的指针域,令其指向第i个结点
- 修改结点*p中的指针域,令其指向*s
核心语句:
① s->next=p->next;
② p->next=s;
仅需修改其前驱的指针

bool ListInsert(LinkNode *&L,int i,ElemType e)
{ int j=0;
LinkList *p=L,*s;
if(i<=0) return false;
while (j<i-1 && p!=NULL) /*查找第i-1个结点*/
{ j++;
p=p->next;
}
if (p==NULL) return false; /*未找到位序为i-1的结点*/
else /*找到位序为i-1的结点*p*/
{ s=(LinkNode *)malloc(sizeof(LinkNode));
/*创建新结点*s*/
s->data=e;
s->next=p->next; /*将*s插入到*p之后*/
p->next=s;
return true;
}
}
- 该算法的关键是找到第i-1个结点,主要操作是移动指针,从头结点开始,直到找到或表结束为止;
- 时间复杂度为O(n)
(9) 删除数据元素ListDelete(&L,i,&e)
描述:删除单链表的第i个结点
操作步骤:
- 找到第i-1个结点*p
- 修改结点*p的指针域,令其指向结点*p 的后继的后继
- 释放第i个结点

核心语句:
p->next = p->next->next;
free( ?);
仅需修改其前驱的指针
bool ListDelete(LinkNode *&L,int i,ElemType &e)
{ int j=0;
LinkNode *p=L,*q;
if(i<=0) return false;
while (j<i-1 && p!=NULL) /*查找第i-1个结点*/
{ j++;
p=p->next;
}
if (p==NULL) return false; /*未找到位序为i-1的结点*/
else /*找到位序为i-1的结点*p*/
{ q=p->next; /*q指向要删除的结点*/
if (q==NULL) return false;
/*若不存在第i个结点,返回0*/
e=q->data;
p->next=q->next; /*从单链表中删除*q结点*/
free(q); /*释放*q结点*/
return true;
}
} 建立单链表
链表与顺序表不同,是一种动态管理的存储结构,链表中每个结点占用的存储空间不是预先分配,而是运行时系统根据需求生成;
- 头插法(逆序) 每次将新结点插入到当前链表的表头,即头结点和第一个元素结点之间
- 尾插法 (顺序) 每次将新结点插入到当前链表的表尾
-
1. 头插法
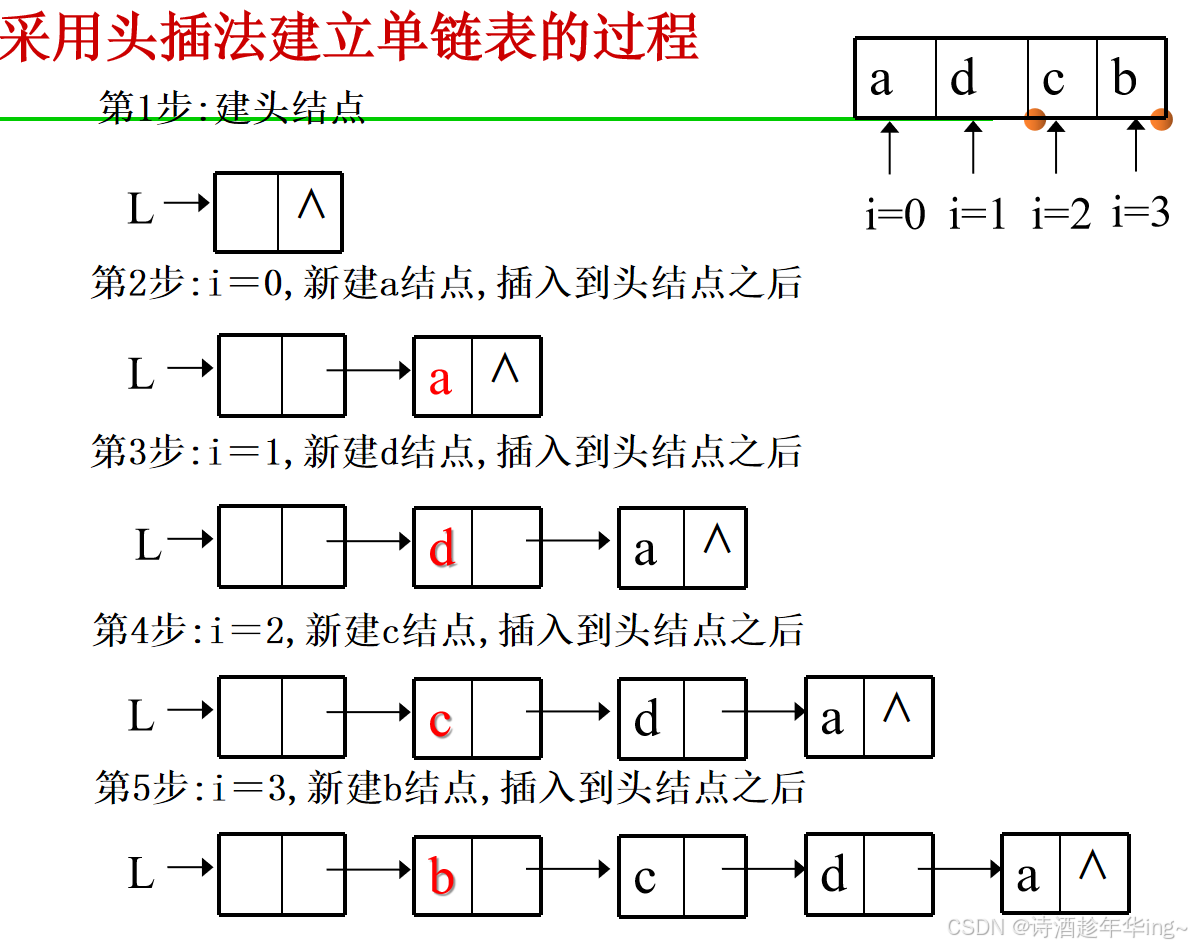
void CreateListF(LinkNode *&L,ElemType a[],int n)
{ LinkNode *s;
L=(LinkList *)malloc(sizeof(LinkList));
L->next=NULL;
for (int i=0;i<n;i++)
{ s=(LinkNode *)malloc(sizeof(LinkNode));
/*创建新结点*/
s->data=a[i];
s->next=L->next;
/*将*s插在原开始结点之前,头结点之后*/
L->next=s;
}
}
头插法建立链表虽然算法简单,但生成的链表中结点的次序和原数组元素的顺序相反。

-
2. 尾插法
将新结点插入到当前链表的表尾上,为此必须增加一个尾指针r,使其始终指向当前链表的尾结点。

- 带头结点的单链表的尾插法
- 由于存在头结点,因此不需要单独维护尾指针。
- 在进行尾插时,同样创建新节点,并将其
next指针设置为NULL。 - 然后,从头结点开始遍历链表,直到找到最后一个节点(即
next为NULL的节点)。 - 将最后一个节点的
next指针指向新节点,完成插入。 - 由于头结点始终存在,因此不需要担心链表为空的情况。
void CreateListR1(LinkNode *&L,ElemType a[],int n)
{
LinkNode *s,*r;
L=(LinkNode *)malloc(sizeof(LinkNode));
r=L; /*r始终指向终端结点,开始时指向头结点*/
for (int i=0;i<n;i++)
{ s=(LinkNode *)malloc(sizeof(LinkNode));
/*创建新结点*/
s->data=a[i]; r->next=s; /*将*s插入*r之后*/
r=s;
}
r->next=NULL; /*尾结点next域置为NULL*/
}
- 不带头结点的单链表的尾插法
- 在进行尾插时,需要维护一个尾指针(tail),该指针始终指向链表的最后一个节点。
- 当插入新节点时,首先创建新节点,并将其
next指针设置为NULL。 - 然后,将尾指针的
next指向新节点,并将尾指针更新为新节点。 - 如果链表为空(即头指针为
NULL),则直接将头指针指向新节点,并更新尾指针为新节点。
void CreateListR2(LinkNode *&L,ElemType a[],int n)
{ LinkNode *s,*r;
r=L=NULL;
for (int i=0;i<n;i++)
{ s=(LinkNode*)malloc(sizeof(LinkNode)); /*创建新结点*/
s->data=a[i];
if(L==NULL) L=s; //第一个结点的处理
else r->next=s; /*将*s插入*r之后*/
r=s;
}
if(r!=NULL) r->next=NULL; /*尾结点next域置为NULL*/
}
- 链式结构的特点

2.2.3双链表
- 目的:查找前驱的时间复杂度为O(1)
- 实现:每个结点中增加一个指向前驱的指针域,使链表可以进行双方向查找
- 用这种结点结构组成的链表称为双链表

结点的结构图:
- struct DNode *prior; /*指向前驱结点*/
typedef struct DNode /*定义双链表结点类型*/
{ ElemType data;
struct DNode *prior; /*指向前驱结点*/
struct DNode *next; /*指向后继结点*/
} DLinkNode;
(1)建立双链表
两种方法:头插法和尾插法
- 头插法
//<1>头插法建立双链表
void CreateListF(DLinkNode*& L, ElemType a[], int n)
{
DLinkNode* s;//待插入结点
//(1)创建头结点
L = (DLinkNode*)malloc(sizeof(DLinkNode));
L->next = L->prior = NULL;
//(2) 插入操作
for (int i = 0; i < n; i++)
{
s= (DLinkNode*)malloc(sizeof(DLinkNode));
s->data = a[i];
s->next = L->next;//第一步:新结点的next指向第一个结点
if (L->next != NULL)//第二步,第一个结点的前驱结点指向新结点
L->next->prior = s;
L->next = s;//第三步修改头结点的next
s->prior = L;//最后修改新结点的前驱结点
}
}- 尾插法
//<2>尾插法建立双链表
void CreateListR(DLinkNode*& L, ElemType a[], int n)
{
DLinkNode* s, * r;
L = (DLinkNode*)malloc(sizeof(DLinkNode));
L->next = L->prior = NULL;
r = L;//r始终指向尾结点,开始指向L
for (int i = 0; i < n; i++)
{
s= (DLinkNode*)malloc(sizeof(DLinkNode));
s->data = a[i];
r->next = s;//第一步将尾部节点的后继指针指向新结点
s->prior = r;//第二步将新结点的前驱指针指向尾部节点
r = s;//最后移动尾指针
}
r->next = NULL;
}(2)插入

s->next=p->next; // 1
p->next-prior=s; // 2
s->prior=p; // 3
p->next=s; // 4

(3)删除

p->next=q->next;
q->next->prior=p;






















 2849
2849

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








