数字三角形

P1216 数字三角形

题目描述

观察下面的数字金字塔。

写一个程序来查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。

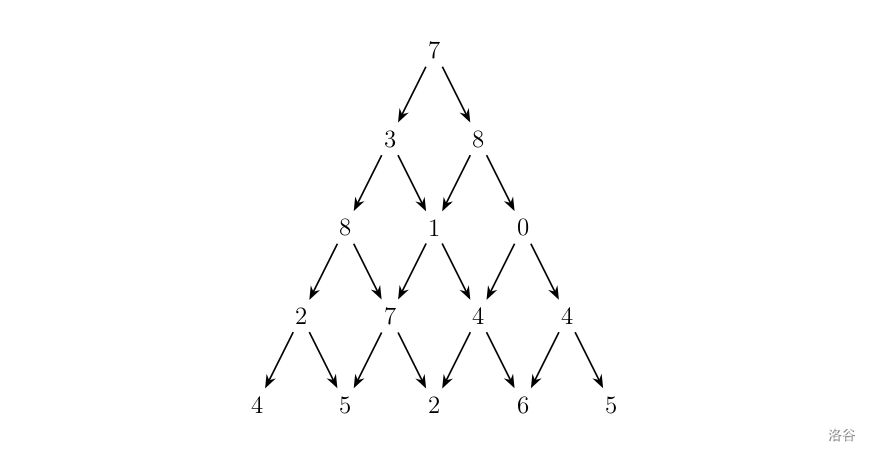
在上面的样例中，从 $7\to 3\to 8\to 7\to 5$ 的路径产生了最大权值。

输入格式

第一个行一个正整数 $r$ ,表示行的数目。

后面每行为这个数字金字塔特定行包含的整数。

输出格式

单独的一行,包含那个可能得到的最大的和。

样例 #1

样例输入 #1

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

样例输出 #1

30

提示

【数据范围】
对于 $100\%$ 的数据，$1\le r\le 1000$，所有输入在 $[0,100]$ 范围内。

题目翻译来自NOCOW。

USACO Training Section 1.5

IOI1994 Day1T1

题解

#include<bits/stdc++.h>
#define ll long long
#define Int __int128
#define pb push_back
#define eb emplace_back
#define ff first
#define ss second
#define M1 20
#define M2 1010
#define M3 5005
#define RI register int
#define ull unsigned long long
#define isc ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);
using namespace std;
const int inf = 0x3f3f3f3f;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
typedef pair<ll, ll> pll;
typedef pair<int, int>pii;
int gcd(int a, int b)
{
    while ((a %= b) && (b %= a));
    return a + b;
}//最大公约数函数
int  spid(int a, int b, int p = mod)
{
    int ans = 1;
    while (b)
    {
        if (b & 1)ans = ans * a % p;
        b >>= 1;
        a = a * a % p;
    }
    return ans;
}//快速幂函数


int r;
int a[M2][M2], f[M2][M2],ans = 0;
void dfs1(int x, int y, int c) {//从下向上
    if (x == r+1) { if (ans < c)ans = c; return; }
    dfs1(x + 1, y, c + a[x][y]);
    dfs1(x + 1, y + 1, c + a[x][y]);
}
//在此处记得要初始化f数组的值为-1，不然若a数组的值全为0与dfs1()并无区别，也会超时
int dfs2(int x,int y){
    if(f[x][y]!=-1)return f[x][y];//记忆化搜索的关键
    if(x==r){f[x][y]=a[x][y];}
    else f[x][y]=a[x][y]+max(dfs2(x+1,y),dfs2(x+1,y+1));
    return f[x][y];
}
void solve() {
    cin >> r;
    for (int i = 1; i <= r; ++i)
        for (int j = 1; j <= i; ++j)
            cin >> a[i][j];
    dfs1(1, 1, 0);
    //在此处记得要初始化f数组的值为-1，不然若a数组的值全为零与dfs1()并无区别，也会超时
    memset(f,-1,sizeof(f));
    dfs2(1,1);
    //还有一个递推从下方向上a[x][y]+=max(a[x+1][y],a[x+1][y+1])
    for(int x=r-1;x>=1;x--)
        for(int y=1;y<=x;y++)
            a[x][y]+=max(a[x+1][y],a[x+1][y+1]);
    cout << ans << endl;
    cout<<f[1][1]<<endl;
    cout<<a[1][1]<<endl;
}
int main() {
    int t = 1;
    //cin>>t;
    while (t--)solve();
}

cout<<f[1][1]<<endl;
cout<<a[1][1]<<endl;
}
int main() {
int t = 1;
//cin>>t;
while (t–)solve();
}