常见加密与逆向分析总结

Ao_tem

已于 2024-04-16 10:11:27 修改

阅读量1.4k

点赞数 12

文章标签：算法密码学网络安全

于 2024-04-15 19:51:47 首次发布

本文链接：https://blog.youkuaiyun.com/2301_81223471/article/details/137793115

版权

错误或有什么需要改进的地方请指正！

base64

不换表

最常见的加密（也不算是加密吧），可以根据查看程序的字符串发现（如果这个遍历没有被引用，大概率没换表）。

主要就是通过有没有base表判断，同时对于+3 /3这种操作也要敏感

换表

根据字符串画面然后查看交叉引用看看有没有进行什么操作，就可以判断是否进行了换表

或者说就是在看程序的函数的时候可以直接看到换过的表

z3

一般在看见矩阵的时候就需要用到z3了，这个比较容易辨别

AES加密
参考资料

AES加密也比较常见，主要可以分为密钥拓展字节替换行移位列混合轮密钥加等五个步骤

1 密钥拓展原始密钥一般比较短比如16字节而算法如果进行10轮运算的话需要16*（10+1）字节长度的密钥需要对原始密钥进行拓展

2 一个非线性的替换步骤根据查表把一个字节换位另一个字节

3 行移位将数据矩阵的每一行循环移位一定长度

4 列混合将数据矩阵乘以一个固定的矩阵增加混淆程度

5 轮密钥加将数据矩阵和密钥矩阵进行异或操作

加密流程

密钥拓展

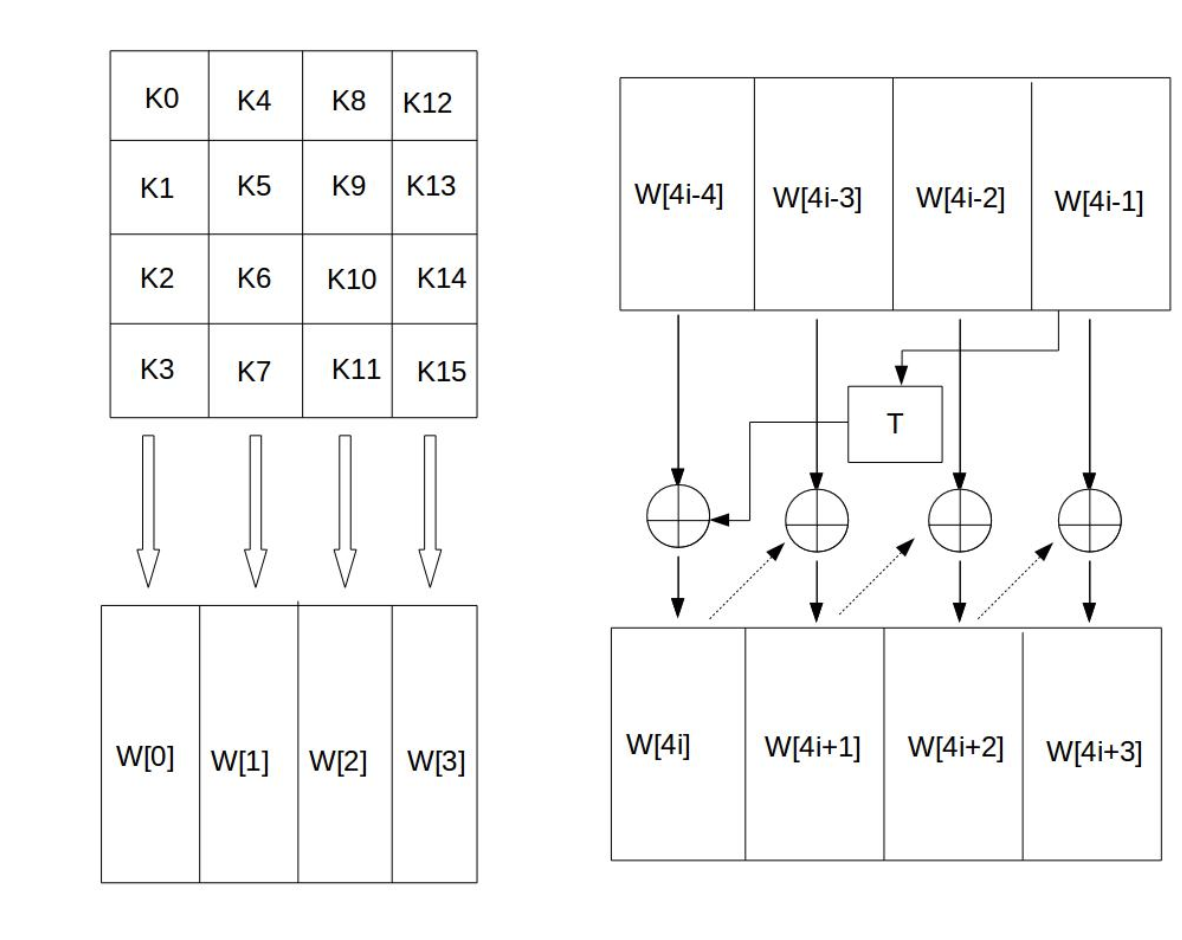
密钥拓展会将初始密钥传入一个4*4的状态矩阵然后会将每列的4个字节组成一个字，

矩阵形成4个字，命名为w[0,1,2,3],假设密钥k为：abcdefghijklmnop 则

k[0]为a k[1]为b k[2]为c k[3]为d 则w[0]为abcd 这个44矩阵的每一列的4个字节组成一个字，矩阵4列的4个字依次命名为W[0]、W[1]、W[2]和W[3]，它们构成一个以字为单位的数组W。例如，设密钥K为"abcdefghijklmnop",则K0 = ‘a’,K1 = ‘b’, K2 = ‘c’,K3 = ‘d’,W[0] = “abcd”。

接着，对W数组扩充40个新列，构成总共44列的扩展密钥数组。新列以如下的递归方式产生：

1.如果i不是4的倍数，那么第i列由如下等式确定：

W[i]=W[i-4]⨁W[i-1]

2.如果i是4的倍数，那么第i列由如下等式确定：

W[i]=W[i-4]⨁T(W[i-1])

其中，T是一个有点复杂的函数。

函数T由3部分组成：字循环、字节代换和轮常量异或，这3部分的作用分别如下。

a.字循环：将1个字中的4个字节循环左移1个字节。即将输入字[b0, b1, b2, b3]变换成[b1,b2,b3,b0]。

b.字节代换：对字循环的结果使用S盒进行字节代换。

c.轮常量异或：将前两步的结果同轮常量Rcon[j]进行异或，其中j表示轮数。

轮常量Rcon[j]是一个字，

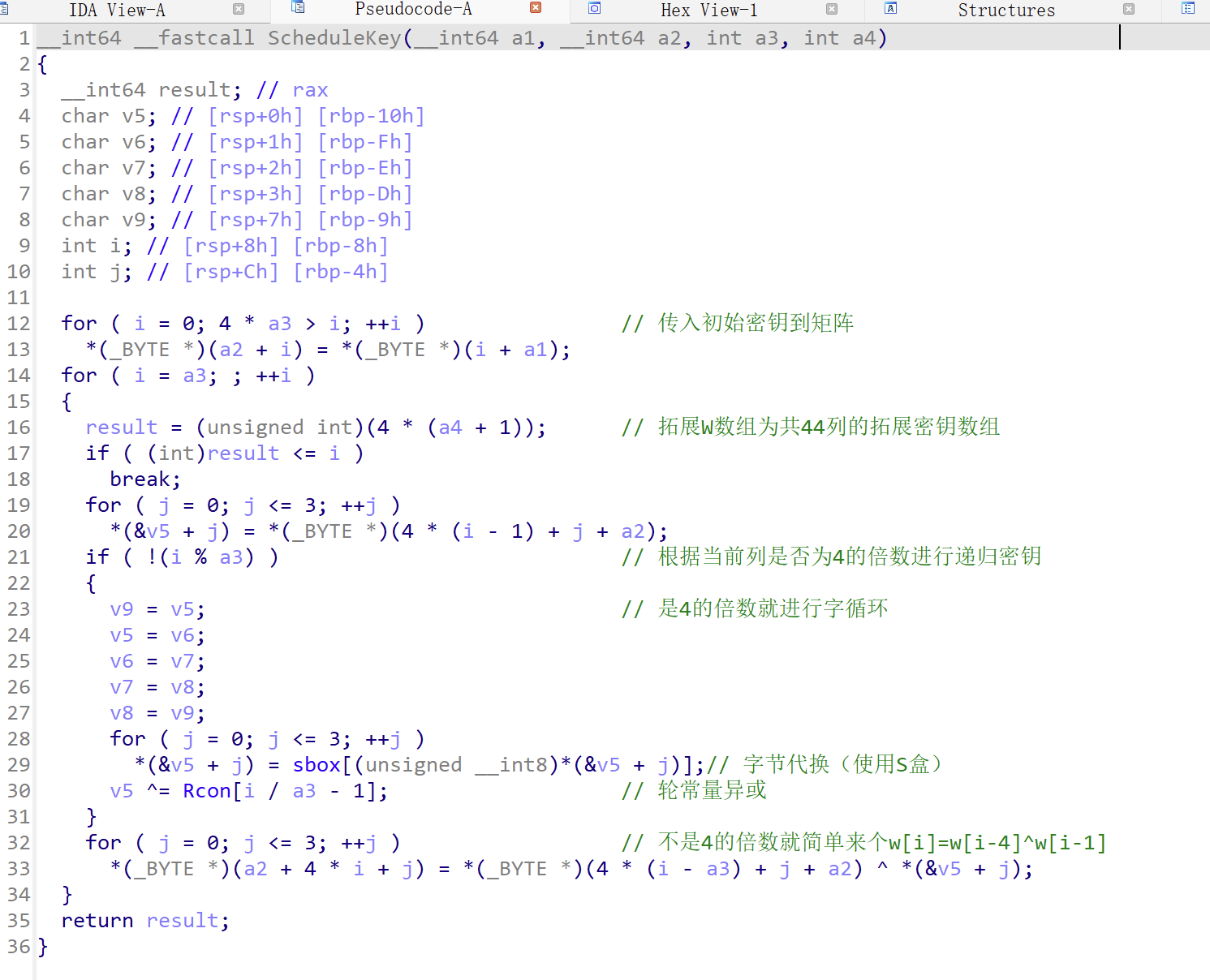
字节替换

（S盒用来加密逆S盒用来解密）

行移位

就是简单的左移

当密钥长度为128比特时，状态矩阵第0行左移位0字节，第1行左移位1字节，第2行左移位2字节......

行移位解密就是右移位相同字节

列混合

轮密钥加

这就死AES的加密流程，可以根据这判断是否是AES加密

RC4加密

RC4是一种对称加密，通过密钥key和s盒生成密钥流，明文逐字节异或s盒，同时s盒也会发生变化

加密和解密使用相同的函数和密钥k

RC4的一些关键变量

1 S-Box也就是S盒，一个长度为256的数组，每个单元长度为一个字节

2 密钥K，密钥的长度与明文长度盒密钥流长度无直接关系

3 临时向量k也是256字节，每个单元也是一个字节，如果密钥长度为256字节，就直接把密钥的值赋给k，否则，轮转地将密钥的每个字节赋给k

代码来自1

RC4加密流程

RC4初始化

进入rc4_init函数

1 初始化一个256字节的数组用来存放S盒

2 填充T盒，不满256字节就填充到256字节

3 交换 s[i]与s[j] i 从0开始一直到255下标结束. j是 s[i]与T[i]组合得出的下标。

这样S盒就被打乱了

RC4加密

RC4加密其实就是遍历数据,将数据与sbox进行异或加密,而在此之前还需要交换一次sbox的数据

交换完之后再把s[i] + s[j]的组合当做下标再去异或.

	for(dn=0;dn<datalen;dn++)
	{
		//i确保S-box的每个元素都得到处理，j保证S-box的搅乱是随机的。 1
		i=(i+1)%256;                                             
		j=(j+rc4.s_box[i])%256;
		
		//交换 s_box[i] 和 s_box[j]								2
		tmp=rc4.s_box[i];                             
		rc4.s_box[i] = rc4.s_box[j];
		rc4.s_box[j] = tmp;
		
		//交换完之后 再把s[i] + s[j]的组合当做下标再去异或.		3
		t = (rc4.s_box[i] + rc4.s_box[j]) % 256;
		data[dn] ^= rc4.s_box[t];
	 }

RC4加密的识别特点

长度为256的数组的创建

TEA家族加密

tea加密一次操作8字节的数据，以16字节的数据为key，算法采用迭代的方式，推荐的迭代次数为64轮，最少32轮（可以迭代），你记住 TEA系列算法中均使用了一个DELTA常熟，但DELTA的值对算法并无什么影响，只是为了避免不良的取值，推荐DELTA的值取为黄金分割数与232的乘积，取整后的十六进制值为0x9e3779B9（也可以改变），算了你记不住，你就记住会有一个常速作为特征值就行了。

TEA家族：

XTEA：使用与TEA相同的简单运算，但四个子密钥采取不正规的方式进行混合以组织密钥表攻击。

Block TEA：Block TEA算法可以对32位任意整数倍长度的变量块进行加解密的操作，该算法将XTEA轮循函数一次应用于块中的每个字，并且将它附加于被应用字的邻字。

XXTEA：XTEEA使用跟Block TEA相似的结构，但在处理块中每个字时利用了相邻字，且用拥有两个输入量的MX函数代替了XTEA轮循函数。上面提到的相邻字实际上就是数组中相邻的项。

只要会处理TEA，XTEA和XXTEA也是同理。

TEA加密

TEA最好识别，他需要一个函数加密，这个函数的第一个参数为待加密的数据，第二个数据为密钥，

待加密的数据为8个字节分为两组，一组4字节加密，密钥为16字节

常规的TEA加密还需要一个常数，0x9e3779b9为迭代的轮数的倍数

为什么是0x61C88647 因为+0x9e3779b9 和 -0x61C88647 等价

需要注意，这个常数可变。

TEA的加密就是移位和异或

解密就是

+=改为-= 左移位变右移位

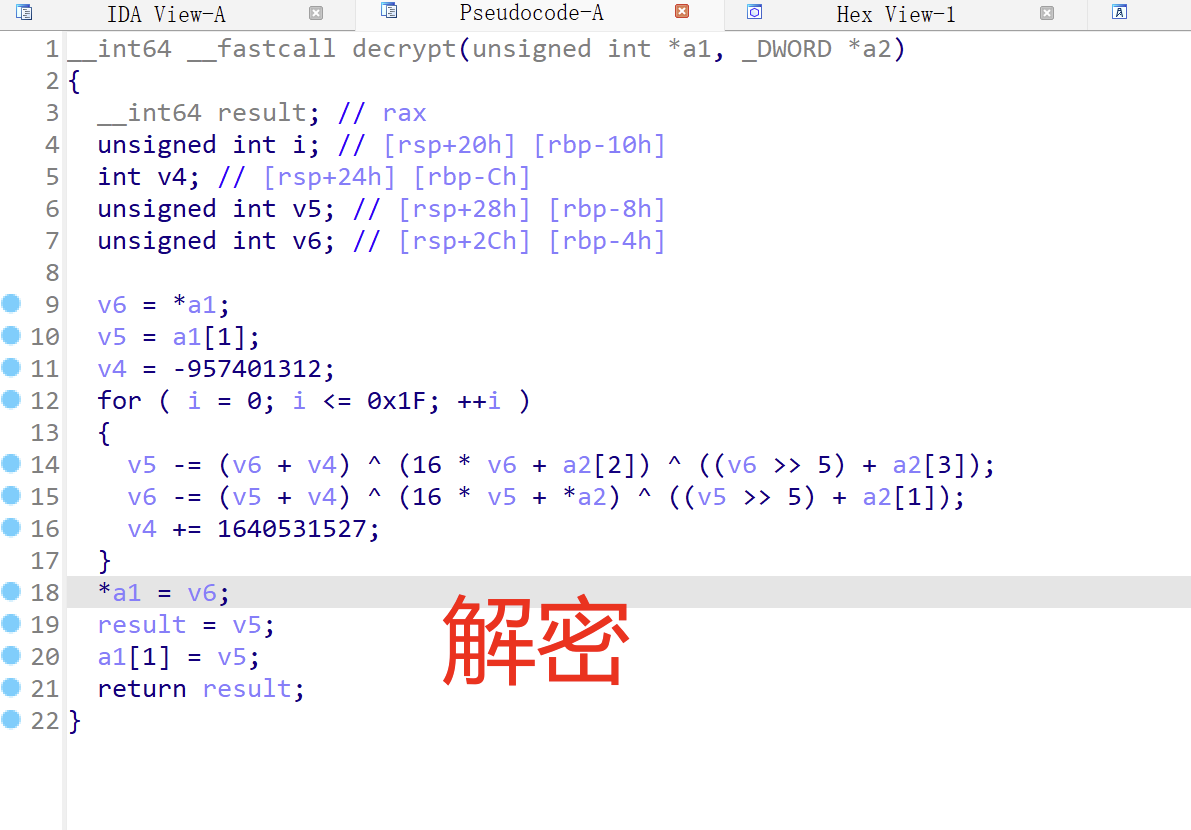
XTEA

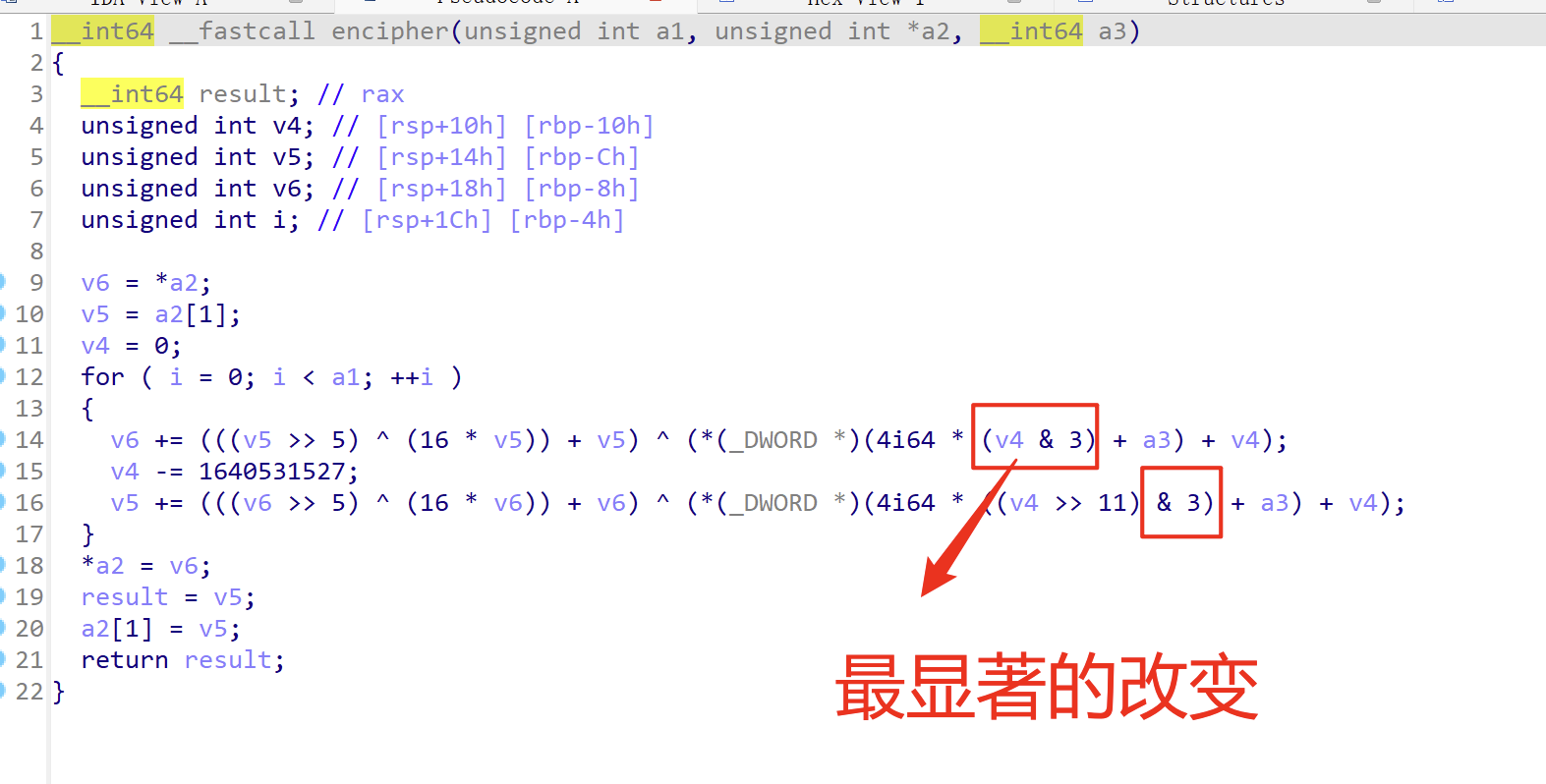
大同小异的感觉

XXTEA

xxtea加密的数据的大小不再固定，可以为32位的倍数（最少64），密钥长度没变

加密的算法的复杂程度较前两个有较大区别

__int64 __fastcall btea(unsigned int *a1, int a2, __int64 a3)
{
  unsigned int *v3; // rax
  unsigned int *v4; // rax
  __int64 result; // rax
  unsigned int *v6; // rax
  int v7; // [rsp+8h] [rbp-18h]
  unsigned int v8; // [rsp+8h] [rbp-18h]
  int v9; // [rsp+Ch] [rbp-14h]
  int v10; // [rsp+Ch] [rbp-14h]
  unsigned int j; // [rsp+10h] [rbp-10h]
  int i; // [rsp+10h] [rbp-10h]
  unsigned int v13; // [rsp+14h] [rbp-Ch]
  unsigned int v14; // [rsp+14h] [rbp-Ch]
  unsigned int v15; // [rsp+18h] [rbp-8h]
  unsigned int v16; // [rsp+18h] [rbp-8h]
  unsigned int v17; // [rsp+18h] [rbp-8h]
  unsigned int v18; // [rsp+1Ch] [rbp-4h]
  unsigned int v19; // [rsp+1Ch] [rbp-4h]
  int v20; // [rsp+38h] [rbp+18h]

  if ( a2 <= 1 )
  {
    if ( a2 < -1 )
    {
      v20 = -a2;
      v10 = 52 / -a2 + 6;
      v14 = -1640531527 * v10;
      v19 = *a1;
      do
      {
        v8 = (v14 >> 2) & 3;
        for ( i = v20 - 1; i; --i )
        {
          v16 = a1[i - 1];
          v6 = &a1[i];
          *v6 -= (((4 * v19) ^ (v16 >> 5)) + ((v19 >> 3) ^ (16 * v16))) ^ ((v19 ^ v14)
                                                                         + (v16 ^ *(_DWORD *)(4i64 * (v8 ^ i & 3) + a3)));
          v19 = *v6;
        }
        v17 = a1[v20 - 1];
        *a1 -= (((4 * v19) ^ (v17 >> 5)) + ((v19 >> 3) ^ (16 * v17))) ^ ((v19 ^ v14)
                                                                       + (v17 ^ *(_DWORD *)(4i64 * v8 + a3)));
        result = *a1;
        v19 = *a1;
        v14 += 1640531527;
        --v10;
      }
      while ( v10 );
    }
  }
  else
  {
    v9 = 52 / a2 + 6;
    v13 = 0;
    v15 = a1[a2 - 1];
    do
    {
      v13 -= 1640531527;
      v7 = (v13 >> 2) & 3;
      for ( j = 0; a2 - 1 > j; ++j )
      {
        v18 = a1[j + 1];
        v3 = &a1[j];
        *v3 += (((4 * v18) ^ (v15 >> 5)) + ((v18 >> 3) ^ (16 * v15))) ^ ((v18 ^ v13)
                                                                       + (v15 ^ *(_DWORD *)(4i64 * (v7 ^ j & 3) + a3)));
        v15 = *v3;
      }
      v4 = &a1[a2 - 1];
      *v4 += (((4 * *a1) ^ (v15 >> 5)) + ((*a1 >> 3) ^ (16 * v15))) ^ ((*a1 ^ v13)
                                                                     + (v15 ^ *(_DWORD *)(4i64 * (v7 ^ j & 3) + a3)));
      result = *v4;
      v15 = result;
      --v9;
    }
    while ( v9 );
  }
  return result;
}

解密对加密算法对数据处理的顺序倒置，加法改减法

__int64 __fastcall btea(unsigned int *a1, int a2, __int64 a3)
{
  unsigned int *v3; // rax
  unsigned int *v4; // rax
  __int64 result; // rax
  unsigned int *v6; // rax
  int v7; // [rsp+8h] [rbp-18h]
  unsigned int v8; // [rsp+8h] [rbp-18h]
  int v9; // [rsp+Ch] [rbp-14h]
  int v10; // [rsp+Ch] [rbp-14h]
  unsigned int j; // [rsp+10h] [rbp-10h]
  int i; // [rsp+10h] [rbp-10h]
  unsigned int v13; // [rsp+14h] [rbp-Ch]
  unsigned int v14; // [rsp+14h] [rbp-Ch]
  unsigned int v15; // [rsp+18h] [rbp-8h]
  unsigned int v16; // [rsp+18h] [rbp-8h]
  unsigned int v17; // [rsp+18h] [rbp-8h]
  unsigned int v18; // [rsp+1Ch] [rbp-4h]
  unsigned int v19; // [rsp+1Ch] [rbp-4h]
  int v20; // [rsp+38h] [rbp+18h]

  if ( a2 <= 1 )
  {
    if ( a2 < -1 )
    {
      v20 = -a2;
      v10 = 52 / -a2 + 6;
      v14 = -1640531527 * v10;
      v19 = *a1;
      do
      {
        v8 = (v14 >> 2) & 3;
        for ( i = v20 - 1; i; --i )
        {
          v16 = a1[i - 1];
          v6 = &a1[i];
          *v6 -= (((4 * v19) ^ (v16 >> 5)) + ((v19 >> 3) ^ (16 * v16))) ^ ((v19 ^ v14)
                                                                         + (v16 ^ *(_DWORD *)(4i64 * (v8 ^ i & 3) + a3)));
          v19 = *v6;
        }
        v17 = a1[v20 - 1];
        *a1 -= (((4 * v19) ^ (v17 >> 5)) + ((v19 >> 3) ^ (16 * v17))) ^ ((v19 ^ v14)
                                                                       + (v17 ^ *(_DWORD *)(4i64 * v8 + a3)));
        result = *a1;
        v19 = *a1;
        v14 += 1640531527;
        --v10;
      }
      while ( v10 );
    }
  }
  else
  {
    v9 = 52 / a2 + 6;
    v13 = 0;
    v15 = a1[a2 - 1];
    do
    {
      v13 -= 1640531527;
      v7 = (v13 >> 2) & 3;
      for ( j = 0; a2 - 1 > j; ++j )
      {
        v18 = a1[j + 1];
        v3 = &a1[j];
        *v3 += (((4 * v18) ^ (v15 >> 5)) + ((v18 >> 3) ^ (16 * v15))) ^ ((v18 ^ v13)
                                                                       + (v15 ^ *(_DWORD *)(4i64 * (v7 ^ j & 3) + a3)));
        v15 = *v3;
      }
      v4 = &a1[a2 - 1];
      *v4 += (((4 * *a1) ^ (v15 >> 5)) + ((*a1 >> 3) ^ (16 * v15))) ^ ((*a1 ^ v13)
                                                                     + (v15 ^ *(_DWORD *)(4i64 * (v7 ^ j & 3) + a3)));
      result = *v4;
      v15 = result;
      --v9;
    }
    while ( v9 );
  }
  return result;
}