矩阵乘法
时间限制:1000ms 内存限制:65535KB
提交总数:65 通过数量:41
提交代码查看记录去讨论
题目描述
给出两个矩阵A和B,求两个矩阵相乘的结果C
相乘的方法是:假设矩阵A是n行m列的矩阵,矩阵B是m行k列的矩阵,矩阵C会得到一个n行k列的矩阵。
矩阵C中第i行,第j列的元素,值为:矩阵A的第i行,与矩阵B的第j列的对应元素,相乘相加的结果。
例如:A是4行3列的矩阵,B是3行2列的矩阵。
矩阵A为:
1 2 3
4 5 6
1 1 1
2 2 2
矩阵B为:
6 5
7 1
8 8
则:
C[1][1]=1*6+2*7+3*8=6+14+24=44; C[1][2]=1*5+2*1+3*8=5+2+24=31;
C[2][1]=4*6+5*7+6*8=24+35+48=107; C[2][2]=4*5+5*1+6*8=20+5+48=73;
C[3][1]=1*6+1*7+1*8=6+7+8=21; C[3][2]=1*5+1*1+1*8=5+1+8=14;
C[4][1]=2*6+2*7+2*8=12+14+16=42; C[4][2]=2*5+2*1+2*8=10+2+16=28;
输入格式
第一行三个正整数 n,m,k。( 0 < n,m,k < 100)
接下来的n行,每行m个数,表示矩阵A。
在后面的m行,每行k个数,表示矩阵B。
输出格式
输出矩阵C。
样例输入
4 3 2
1 2 3
4 5 6
1 1 1
2 2 2
6 5
7 1
8 8
样例输出
44 31
107 73
21 14
42 28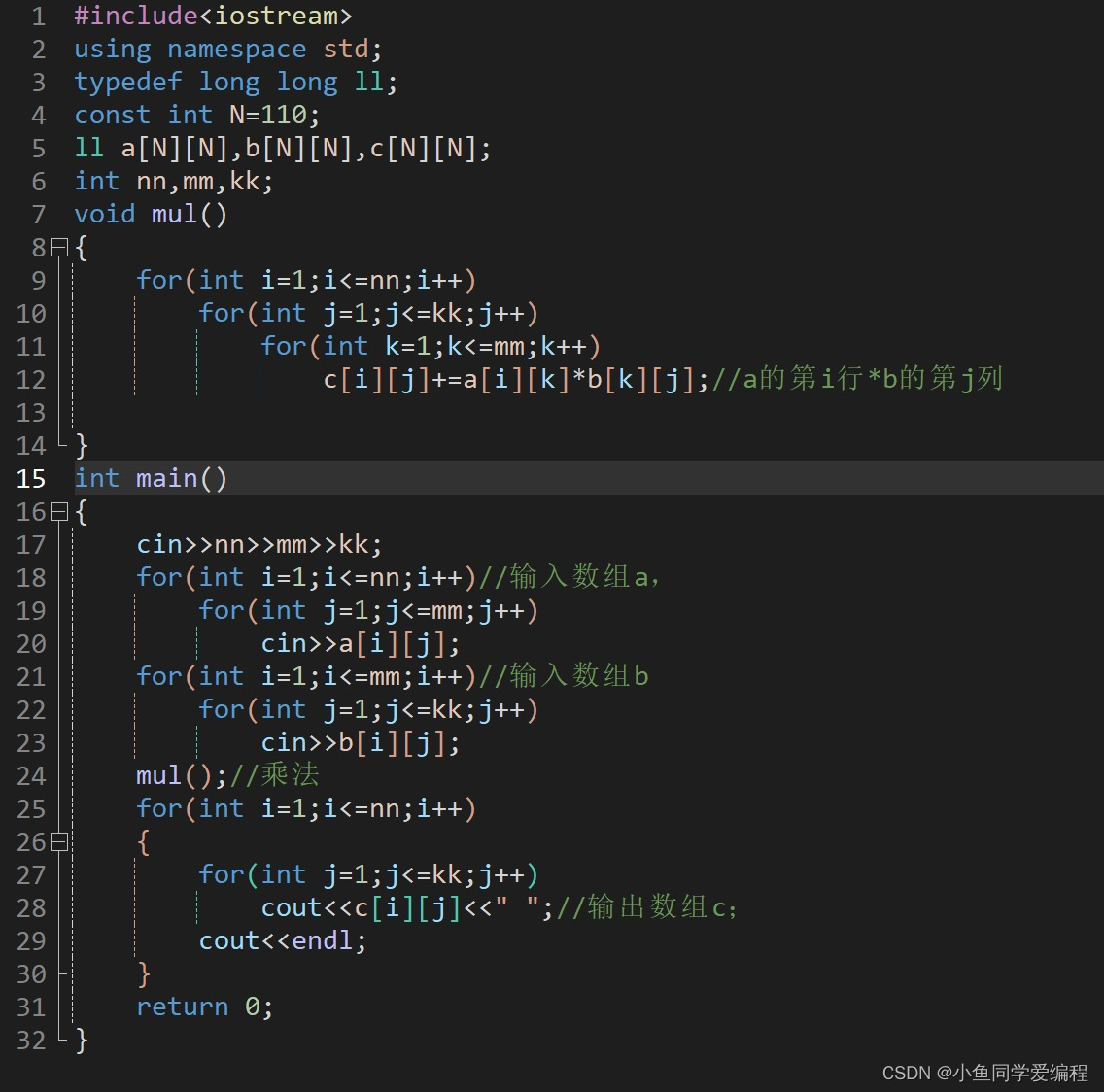




 本文介绍了如何通过编程实现矩阵乘法,给出了矩阵A和B的示例,以及输入和输出的格式要求。重点在于理解矩阵乘法规则并用代码表示计算过程。
本文介绍了如何通过编程实现矩阵乘法,给出了矩阵A和B的示例,以及输入和输出的格式要求。重点在于理解矩阵乘法规则并用代码表示计算过程。
















 1610
1610










