特征工程 -- Feature Engineering！（Kaggle学习教程）

Part1 -- What Is Feature Engineering

特征工程的目标

-- 使你的数据更适合当前的问题

特征工程的好处

1.提高模型的预测性能（在竞赛中最为重要）

2.减少计算或数据需求

3.提高结果的可解释性（在未来业务中会很重要）

特征工程的指导原则

      要使功能有用，它必须与模型能够学习的目标建立关系。例如，线性模型只能学习线性关系。因此，在使用线性模型时，您的目标是转换特征以使它们与目标的关系呈线性关系。

       因此特征工程的关键思想是 -- 应用于特征的转换实质上成为模型本身的一部分。

For example:假设你试图根据一侧的长度来预测方形土地的价格。将线性模型直接拟合到 Length 会得到较差的结果，因为关系不是线性的；但是，如果我们将 Length 特征平方以获得 'Area'，我们将创建一个线性关系。将 Area 添加到特征集意味着该线性模型现在可以拟合抛物线。换句话说，对特征进行平方使线性模型能够拟合平方特征。

---------------------------------------------------------------------------------------------------------------------------------

示例 --  Concrete dataset

import pandas as pd
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import cross_val_score

df = pd.read_csv("../input/fe-course-data/concrete.csv")
df.head()

我们首先将以上未进行增强的数据集上来训练模型以此建立基线 -- 这将会在后续帮助我们来判断我们新构建的特征是否真的有助于模型提升性能

X = df.copy()
y = X.pop("CompressiveStrength")

# 训练模型并计算出基线分数
baseline = RandomForestRegressor(criterion="absolute_error", random_state=0)
baseline_score = cross_val_score(
    baseline, X, y, cv=5, scoring="neg_mean_absolute_error"
)
baseline_score = -1 * baseline_score.mean()

print(f"MAE Baseline Score: {baseline_score:.4}")

MAE Baseline Score: 8.232

接下来，我们根据生活常识，来分别计算三个新的比例关系

X = df.copy()
y = X.pop("CompressiveStrength")

# Create synthetic features
X["FCRatio"] = X["FineAggregate"] / X["CoarseAggregate"]
X["AggCmtRatio"] = (X["CoarseAggregate"] + X["FineAggregate"]) / X["Cement"]
X["WtrCmtRatio"] = X["Water"] / X["Cement"]

# Train and score model on dataset with additional ratio features
model = RandomForestRegressor(criterion="absolute_error", random_state=0)
score = cross_val_score(
    model, X, y, cv=5, scoring="neg_mean_absolute_error"
)
score = -1 * score.mean()

print(f"MAE Score with Ratio Features: {score:.4}")

MAE Score with Ratio Features: 7.948

我们发现 MAE分数下降了，因此可以判断模型的性能得到了提升。

Part2 -- Mutual Information

面对一个新的数据集，尤其是在Kaggle官网上的数据集，他的数据集中的特征可能几十列甚至上百列。对于一个新手而言，可能会感到十分的无措以及迷茫，一个很好的开始，一般是由feature utility metric（特征效用指标）来构建排名，该指标是衡量特征与目标之间关联的函数。你可以根据该指标来选择一小部分最有效的特征来进行初步的开发。

我们将使用的指标称为 “mutual information”，他的优势有以下几点：

1.易于使用和解释

2.计算效率高

3.理论上有依据

4.抗拟合能力强

5.能够检测任何类型的关系

互信息（Mutual Information）及其测量内容

互信息从 不确定性 的角度描述关系。两个量之间的互信息(MI) 是衡量一个量的知识在多大程度上减少另一个量的不确定性的量度。

以下将以房价（Ames Housing Dataset）为例：

从图中我们可以看出，知道 ExterQual 的值应该会让你对对应的 SalePrice 更加确定 —— 每个类别的 ExterQual 都倾向于将 SalePrice 集中在某个范围内。ExterQual 与 SalePrice 的互信息是 SalePrice 的不确定性相对于 ExterQual 的四个值的平均减少量。例如，由于 Fair 的出现频率低于 Typical，因此 Fair 在 MI 分数中的权重较低。

解释互信息分数

数量之间可能的最小互信息为 0.0。当 MI 为零时，数量是独立的：两者都不能告诉你关于另一个的任何事情。相反，理论上 MI 没有上限。但在实践中，高于 2.0 左右的值并不常见。（互信息是一个对数，所以它增加得非常慢）

下图将让你了解 MI 值如何与特征与目标的关联类型和程度相对应：

左： 随着特征和目标之间的依赖关系变得更加紧密，互信息也会增加。 

右： 互信息可以捕获任何类型的关联（不仅仅是线性的，比如相关性）。

以下是注意事项：

1.单变量度量 -- MI 只能衡量单个特征与目标变量之间的关系，而不能捕捉特征之间的相互作用。有些特征单独看可能信息量不大，但与其他特征组合时可能变得非常有用。MI 无法检测到这种情况。

2.特征的实际有用性取决于模型 -- 即使某个特征的 MI 值很高，模型也不一定能有效利用它；这取决于模型是否能够学习到该特征与目标变量之间的关系。例如，线性模型可能无法直接利用具有非线性关系的高 MI 特征，而需要进行特征转换。

3.可能需要特征变换 -- MI 高的特征可能需要适当的预处理（如对数变换、分桶、交叉特征等）才能让模型更容易学习到它与目标变量的关系；例如，特征 X 可能与目标 Y 呈指数关系，原始特征的 MI 可能很高，但线性模型无法直接学习到这种关系，需要对 X 取对数后才能更好地被模型利用。

---------------------------------------------------------------------------------------------------------------------------------

示例：1985 Automobiles

# 导入相关库和数据
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns

plt.style.use("seaborn-whitegrid")

df = pd.read_csv("../input/fe-course-data/autos.csv")
df.head()

因为计算互信息（MI）时，必须正确区分离散特征和连续特征，因此我们首先需要进行区分

X = df.copy()
y = X.pop("price")

# 对类别特征进行标签编码（Label Encoding）
for colname in X.select_dtypes("object"):
    X[colname], _ = X[colname].factorize()

# 所有离散特征现在都应该是整数类型（int dtype）！
discrete_features = X.dtypes == int

from sklearn.feature_selection import mutual_info_regression

# 计算互信息的函数
def make_mi_scores(X, y, discrete_features):
    '''
    X , y : 训练数据（特征） , 目标变量
    discrete_features : 离散特征
    '''
    mi_scores = mutual_info_regression(X, y, discrete_features=discrete_features)
    mi_scores = pd.Series(mi_scores, name="MI Scores", index=X.columns)
    mi_scores = mi_scores.sort_values(ascending=False)
    return mi_scores

mi_scores = make_mi_scores(X, y, discrete_features)
mi_scores[::3]  

# 计算出的MI分数进行可视化
def plot_mi_scores(scores):
    scores = scores.sort_values(ascending=True)
    width = np.arange(len(scores))
    ticks = list(scores.index)
    plt.barh(width, scores)
    plt.yticks(width, ticks)
    plt.title("Mutual Information Scores")


plt.figure(dpi=100, figsize=(8, 5))
plot_mi_scores(mi_scores)

该图得出的结论和我们之前发现的一致：curb_weight 特征与目标价格表现出很强的关系！

sns.relplot(x="curb_weight", y="price", data=df);

fuel_type 特征的 MI 分数相当低，但从图中可以看出，它清楚地区分了 fuel_type 中具有不同趋势的两个价格群体。这表明 fuel_type 有助于交互效果，并且可能毕竟不是不重要的。在根据 MI 分数确定某个功能不重要之前，最好调查一下任何可能的交互影响 —— 领域知识可以在这里提供很多指导。

Part3 -- Creating Features

Mathematical Transforms -- 数学变换

数值特征之间的关系通常通过数学公式表示，这是在领域研究中经常遇到的。在 Pandas 中，可以通过对列进行算术运算，就像它们是普通数字一样。

在 Automobile 数据集中，有描述汽车引擎的特征。研究产生了各种公式来创建可能有用的新功能。例如，“冲程比”是衡量发动机效率与性能的指标：

autos["stroke_ratio"] = autos.stroke / autos.bore

注意：组合越复杂，模型就越难学习，就像这个发动机的 “排量” 公式，它是其功率的量度：

autos["displacement"] = (
    np.pi * ((0.5 * autos.bore) ** 2) * autos.stroke * autos.num_of_cylinders
)

数据可视化可以帮助发现需要进行特征变换的情况，通常是通过幂运算或对数变换来“重塑”特征的分布。

accidents["LogWindSpeed"] = accidents.WindSpeed.apply(np.log1p)

# 关系可视化
fig, axs = plt.subplots(1, 2, figsize=(8, 4))
sns.kdeplot(accidents.WindSpeed, shade=True, ax=axs[0])
sns.kdeplot(accidents.LogWindSpeed, shade=True, ax=axs[1]);

上图发现通过对 WindSpeed 进行了对数变换，发现其两者之间的关系有了明显的变化！~

如果你发现了数值特征和分类特征之间的交互效应，则可能需要使用 one-hot 编码（独热编码）对其进行显式建模，如下所示：

# One-hot encode Categorical feature, 添加前缀 -- Cat
X_new = pd.get_dummies(df.Categorical, prefix="Cat")

# 按照行进行逐行相乘
X_new = X_new.mul(df.Continuous, axis=0)

# 连接新的特征
X = X.join(X_new)

Counts -- 计数

描述某物存在与否的特征通常成组出现，例如，一种疾病的风险因素的集合。您可以通过创建计数来聚合此类特征。这些功能将是二进制 （1 表示存在，0 表示不存在）或布尔值 （True 或者 False）。

在 Traffic Accidents 中，有几个特征指示事故附近是否有某个道路物体。这将使用 sum 方法创建附近道路要素总数的计数：

roadway_features = ["Amenity", "Bump", "Crossing", "GiveWay",
    "Junction", "NoExit", "Railway", "Roundabout", "Station", "Stop",
    "TrafficCalming", "TrafficSignal"]
accidents["RoadwayFeatures"] = accidents[roadway_features].sum(axis=1)

accidents[roadway_features + ["RoadwayFeatures"]].head(10)

同时还可以使用 DataFrame 自带的方法来创建布尔值，以分析数据中的特定条件。

在 Concrete Dataset 中，每个配方包含不同成分的数值。例如，某些配方可能缺少某些成分（即某个成分的值为 0）。我们可以利用 Pandas 的 gt() 方法（greater-than，大于）来统计配方中含有成分的个数。

components = [ "Cement", "BlastFurnaceSlag", "FlyAsh", "Water",
               "Superplasticizer", "CoarseAggregate", "FineAggregate"]
# .gt(0) 将成分数据转换为布尔值（True 表示该成分存在，False 表示缺失）
concrete["Components"] = concrete[components].gt(0).sum(axis=1)

concrete[components + ["Components"]].head(10)

Building-Up and Breaking-Down Features -- 构建和分解特征

通常，你会有复杂的字符串，这些字符串可以有效地分解成更简单的部分，例如：

ID numbers: '123-45-6789'

Phone numbers: '(999) 555-0123'

Street addresses: '8241 Kaggle Ln., Goose City, NV'

Internet addresses: 'http://www.kaggle.com

Product codes: '0 36000 29145 2'

Dates and times: 'Mon Sep 30 07:06:05 2013'

像这样的功能通常具有某种您可以使用的结构。例如，美国电话号码有一个区号（“（999）” 部分），告诉您呼叫者的位置。与往常一样，一些研究可以在这里得到提升。

str 访问器允许您将字符串方法（如 split）直接应用于列。Customer Lifetime Value 数据集包含描述保险公司客户的特征。在 Policy 功能中，我们可以将 Type 与 Level of coverage 分开：

customer[["Type", "Level"]] = (  # 创造两列新的特征
    customer["Policy"]           # 通过原始特征'Policy'来创造
    .str                         # 通过 str
    .split(" ", expand=True)     # 用空格来分割 " "
)

customer[["Policy", "Type", "Level"]].head(10)

autos["make_and_style"] = autos["make"] + "_" + autos["body_style"]
autos[["make", "body_style", "make_and_style"]].head()

Group Transforms -- 组变换

最后，我们有 组转换 ，它聚合按某个类别分组的多个行的信息。通过组变换，您可以创建如下功能：“一个人居住州的平均收入”或“按类型划分的工作日上映的电影比例”。如果您发现了类别交互，则对该分类进行组转换可能是值得调查的事情。

使用聚合函数，组转换结合了两个特征：一个提供分组的分类特征和另一个要聚合其值的特征。对于“各州的平均收入”，您可以选择 State 作为分组功能，为  mean 作为聚合函数，并选择 Income 作为聚合功能。为了在 Pandas 中计算这一点，我们使用 groupby 和 transform 方法：

customer["AverageIncome"] = (
    customer.groupby("State")  # 按照每个州来进行分组
    ["Income"]                 # 选择 特征列 'Income'
    .transform("mean")         # 来计算 特征列 'Incomde' 的平均值
)

customer[["State", "Income", "AverageIncome"]].head(10)

mean 函数是一个内置的 DataFrame 方法，这意味着我们可以将其作为字符串传递给 transform。其他方便的方法包括 max、min、median、var、std 和 count。以下是计算数据集中每种状态出现频率的方法：

customer["StateFreq"] = (
    customer.groupby("State")
    ["State"]
    .transform("count")
    / customer.State.count()
)

customer[["State", "StateFreq"]].head(10)

如果您正在使用训练和验证拆分，为了保持其独立性，最好仅使用训练集创建分组特征，然后将其联接到验证集。在训练集上创建一组具有 drop_duplicates 的唯一值后，我们可以使用验证集的 merge 方法：

# 数据集划分
df_train = customer.sample(frac=0.5)
df_valid = customer.drop(df_train.index)

# 在训练集上创造新的特征列
df_train["AverageClaim"] = df_train.groupby("Coverage")["ClaimAmount"].transform("mean")

# 进行数据拼接
df_valid = df_valid.merge(
    df_train[["Coverage", "AverageClaim"]].drop_duplicates(),
    on="Coverage",
    how="left",
)

df_valid[["Coverage", "AverageClaim"]].head(10)

Part4 -- Clustering With K-Means

在Part4和Part5中，我们将学习无监督学习算法。

无监督算法不使用目标，相反，他们的目的是学习数据的某些属性，以某种方式表示特征的结构。在用于预测的特征工程上下文中，您可以将无监督算法视为“特征发现”技术。

聚类只是意味着根据点彼此之间的相似程度将数据点分配给组。例如，当用于特征工程时，我们可以尝试发现代表某个细分市场的客户群，或具有相似天气模式的地理区域。添加集群标签功能可以帮助机器学习模型理清空间或邻近的复杂关系。

Cluster Labels as a Feature -- 聚类标签作为一项特征

聚类应用于单个实值特征，其作用类似于传统的“分箱”或 “离散化” 转换。在多个特征上，它类似于 “多维分箱” （有时称为矢量量化 ）。

左： 对单个特征进行聚类。 右： 跨两个特征的聚类。

Remember，此 Cluster 特征是分类的。在这里，它与典型的聚类算法生成的标签编码（即整数序列）一起显示;根据您的模型，one-hot 编码可能更合适。

添加集群标签的动机 -- 集群会将功能之间的复杂关系分解为更简单的块。然后，我们的模型可以逐个学习更简单的块，而不必一次性学习复杂的整体。这是一种“分而治之”的策略。

对 YearBuilt 功能进行聚类有助于此线性模型了解它与 SalePrice 的关系。

该图显示了聚类如何改进简单的线性模型。YearBuilt 和 SalePrice 之间的弯曲关系对于这种模型来说太复杂了 -- 它不适合 。然而，在较小的块上，关系几乎是线性的，并且模型可以很容易地学习。

k-Means Clustering -- K-means聚类

有很多聚类算法。它们的主要区别在于如何测量 “相似性” 或 “邻近性” 以及它们使用的特征类型。我们将使用的算法 k-means 非常直观，易于在特征工程环境中应用。根据您的应用程序，其他的算法可能更合适。

K-means 聚类使用普通直线距离（即欧几里得距离）来度量相似性。它通过在特征空间内放置许多点（称为质心 ）来创建集群。数据集中的每个点都分配给它最接近的质心的集群。“k-means” 中的 “k” 是它创建的质心 （即集群） 的数量。

你可以想象每个质心通过一系列辐射圆捕获点。当来自竞争质心的圆集重叠时，它们将形成一条线。结果就是所谓的 Voronoi 镶嵌 。

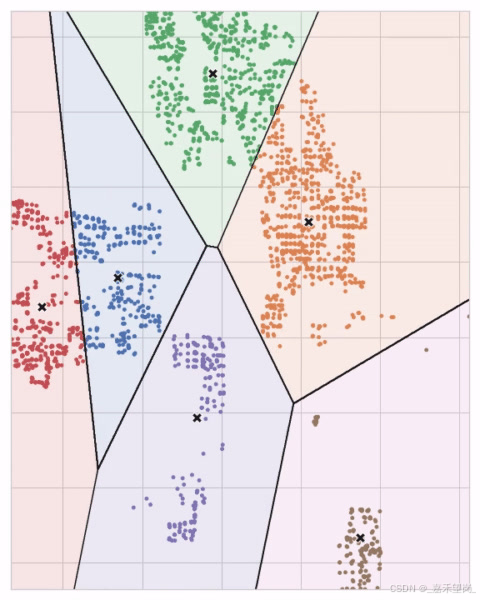
              K-means 聚类创建特征空间的 Voronoi 镶嵌

接下来，让我们回顾一下k-means算法如何学习聚类，以及这对特征工程意味着什么？

我们将重点学习 scikit-learn中的三个参数：n_clusters、max_iter 和 n_init。

首先，该算法会随机初始化一些预定义的 质心数（n_clusters），然后他将持续进行迭代一下两个步骤：

-- 将点分配给最近的聚类质心

-- 移动每个质心以最小化到其点的距离

它会迭代这两个步骤，直到质心不再移动，或者直到经过一些 最大迭代次数（max_iter）停止。

质心的初始随机位置通常以糟糕的聚类结束。因此，该算法将 重复多次（n_init）并返回每个点与其质心之间总距离最小的聚类，即最佳聚类。

可能需要增加大量集群的 max_iter 或复杂数据集的 n_init。通常，需要自己选择的唯一参数是 n_clusters（即 k）。一组特征的最佳分区取决于您使用的模型和您尝试预测的内容，因此最好像调整任何超参数一样对其进行调整（例如，通过交叉验证）。

Scaling Features-- 扩容特征

k-means 算法对规模敏感。这意味着我们需要考虑如何以及是否重新缩放我们的特征，因为根据我们的选择，我们可能会得到非常不同的结果。根据经验，如果要素已经可以直接比较（例如不同时间的测试结果），那么你不会选择重新缩放。另一方面，不在可比尺度上的特征（如身高和体重）通常会从重新缩放中受益。但有时，选择并不明确。在这种情况下，您应该尝试使用常识，记住值较大的特征将受到更重的权重。

以下将举三个例子来帮助你理解什么情况需要进行缩放

请考虑以下功能集。对于每个选项，请决定是否：它应该重新缩放；它们不应该被重新缩放，或者两者都可能是合理的。

加利福尼亚州城市的纬度和经度 -- NO，因为重新缩放会扭曲 Latitude 和 Longitude 描述的自然距离。

爱荷华州艾姆斯房屋的地块面积和生活面积 -- Either，任何一种选择都是合理的，但是由于房屋的居住面积往往每平方英尺更有价值，因此重新调整这些特征的比例是有意义的，这样地块面积在聚类中的权重就不会与其对 SalePrice 的影响不成比例。

1989 年模型汽车的门数和马力 -- Yes，因为这些没有类似的单位。如果不重新缩放，汽车中的车门数量（通常为 2 或 4 个）与马力（通常为数百辆）相比可以忽略不计。

---------------------------------------------------------------------------------------------------------------------------------示例 -- California Housing

作为空间特征， California Housing 的 “纬度” 和 “经度” 是 k-means 聚类的自然候选项。在此示例中，我们将这些与 'MedInc'（收入中位数）聚类，以在加利福尼亚的不同地区创建经济细分。

# Create cluster feature
kmeans = KMeans(n_clusters=6)
X["Cluster"] = kmeans.fit_predict(X)
X["Cluster"] = X["Cluster"].astype("category")

X.head()

在让我们看看几个图，看看这是否有效。首先，显示分类地理分布的散点图。该算法似乎为沿海地区的高收入地区创建了单独的部分。

此数据集中的目标是 MedHouseVal（房屋价值中位数）。这些箱线图显示目标在每个集群中的分布。如果聚类提供了信息，那么这些分布在大多数情况下应该在 MedHouseVal 中分开，这确实是我们所看到的。

X["MedHouseVal"] = df["MedHouseVal"]
sns.catplot(x="MedHouseVal", y="Cluster", data=X, kind="boxen", height=6);

---------------------------------------------------------------------------------------------------------------------------------

X = df.copy()
y = X.pop("SalePrice")

# 选择聚类的特征
features = [
    "LotArea",
    "TotalBsmtSF",
    "FirstFlrSF",
    "SecondFlrSF",
    "GrLivArea",
]

# Standardize
X_scaled = X.loc[:, features]
X_scaled = (X_scaled - X_scaled.mean(axis=0)) / X_scaled.std(axis=0)

# Fit the KMeans model to X_scaled and create the cluster labels
kmeans = KMeans(n_clusters=10, n_init=10, random_state=0)
X["Cluster"] = kmeans.fit_predict(X_scaled)

利用散点图实现聚类可视化

Xy = X.copy()
Xy["Cluster"] = Xy.Cluster.astype("category")
Xy["SalePrice"] = y
sns.relplot(
    x="value", y="SalePrice", hue="Cluster", col="variable",
    height=4, aspect=1, facet_kws={'sharex': False}, col_wrap=3,
    data=Xy.melt(
        value_vars=features, id_vars=["SalePrice", "Cluster"],
    ),
);

Part5--Principal Component Analysis

在Part4中，我们了解到第一种基于模型的特征工程方法 -- 聚类；在本部分，我们将了解主成分分析（PCA），就像聚类是基于邻近度对数据集进行分区一样，你可以将 PCA 视为对数据变化的分区。PCA 是一个很好的工具，可帮助您发现数据中的重要关系，也可用于创建更多信息特征。

说明：PCA 通常应用于标准化数据，因此在本节中，所有数据在应用PCA之前都应该进行标准化

Principal Component Analysis -- 主成分分析

在 Abalone Dataset（鲍鱼数据集）中，鲍鱼的壳的特征是 'Height' 和 'Diameter'

你可以去着试想象：这些数据中有 “变异轴”，它们描述了鲍鱼彼此之间往往不同的方式。在图形上，这些轴显示为沿数据的自然维度延伸的垂直线，每个原始特征对应一个轴。

通常，我们可以为这些变化轴命名。我们可以称为 “Size” 分量的较长轴；同时称为 “Shape” 分量的较短轴。注意：我们用“Size”和“Shape”来描述鲍鱼，而不是“Height”和“Diameter”。因为，这是 PCA 的全部思想：我们不是用原始特征来描述数据，而是用变化轴来描述它。变化轴成为新功能。

新特征 PCA 构造实际上只是原始特征的线性组合（加权和）：

df["Size"] = 0.707 * X["Height"] + 0.707 * X["Diameter"]
df["Shape"] = 0.707 * X["Height"] - 0.707 * X["Diameter"]

这些新特征称为数据的主要组成部分（principal components ） 。权重（weights）本身称为载荷（loadings） 。原始数据集中的特征数量将包含主成分：如果我们使用 10 个特征而不是 2 个，我们最终会得到 10 个成分。

组件（component）的载荷（loadings）告诉我们它通过符号和大小表示的变化：

此载荷表告诉我们，在 Size （大小 ） 组件中，Height （高度 ） 和 Diameter （直径） 方向相同（相同符号），但在 Shape （形状 ） 组件中，它们方向相反（相反符号）。在每个组件中，载荷都具有相同的大小，因此特征在两者中的贡献相同。

PCA 还告诉我们每个组件中的变异量 。从图中我们可以看到，沿 Size 组件的数据变化大于沿 Shape 组件的变化。PCA 通过每个分量的解释方差百分比来精确计算。

Size约占 Height 和 Diameter 之间差异的 96%，Shape约占 4%。

Size组件捕获 Height 和 Diameter之间的大部分变化。但是，请务必记住，组件中的方差量不一定与它作为预测因子的好坏相对应：这取决于您尝试预测的内容。

PCA for Feature Engineering -- 用于特征特征工程的PCA

以下有两种方法可以将PCA应用于特征工程

第一种方法是将其用作描述性技术。因为这些分量告诉您有关变化的信息，因此您可以计算分量的 MI 分数，并查看哪种类型的变化最能预测您的目标。这可以为您提供创建各种特征的想法 - 例如，如果 “Size” 很重要，则为 “Height” 和 “Diameter” 的乘积，如果 Shape 很重要，则为 “Height” 和 “Diameter” 的比率。您甚至可以尝试对一个或多个高分组件进行聚类。

第二种方法是使用组件（components ）本身作为特征。由于这些组件直接公开了数据的变分结构，因此它们通常比原始特征提供的信息更多。以下是一些用例：

1.降维 -- 当您的特征高度冗余（特别是多重共线 ）时，PCA 会将冗余划分为一个或多个接近零的方差分量，然后您可以删除这些分量，因为它们包含的信息很少或没有信息。

2.异常检测 -- 从原始特征中不明显的异常变化通常会显示在低方差分量中。这些组件在异常或异常值检测任务中可能具有高度信息量。

3.降噪 -- 传感器读数的集合通常会共享一些常见的背景噪声。PCA 有时可以将（信息性）信号收集到较少数量的特征中，而忽略噪声，从而提高信噪比。

4.去相关 ：一些机器学习（ML）算法难以处理高度相关的特征。PCA 将相关特征转换为不相关的组件，这可能更容易用于您的算法。

PCA 基本上允许您直接访问数据的相关结构。

PCA 最佳实践 -- 应用PCA时，你需要记住以下几点：

1.PCA 仅适用于数值特征，例如连续数量或计数。

2.PCA 对缩放敏感。最好在应用 PCA 之前对数据进行标准化，除非您知道自己有充分的理由不这样做。

3.考虑删除或限制异常值，因为它们可能会对结果产生不当影响。

---------------------------------------------------------------------------------------------------------------------------------

示例 -- 1985 Automobiles

定义后续会被用到的函数 -- plot_variance 和 make_mi_scores。

# 可视化 PCA的方差解释情况
def plot_variance(pca, width=8, dpi=100):
    # 创建图像
    fig, axs = plt.subplots(1, 2)
    n = pca.n_components_
    grid = np.arange(1, n + 1)

    # E绘制解释方差
    evr = pca.explained_variance_ratio_   # 解释方差比例
    axs[0].bar(grid, evr)
    axs[0].set(
        xlabel="Component", title="% Explained Variance", ylim=(0.0, 1.0)
    )
    # 绘制累计方差
    cv = np.cumsum(evr)
    axs[1].plot(np.r_[0, grid], np.r_[0, cv], "o-")
    axs[1].set(
        xlabel="Component", title="% Cumulative Variance", ylim=(0.0, 1.0)
    )
    # 设置图像
    fig.set(figwidth=8, dpi=100)
    return axs

# 计算 MI 分数
def make_mi_scores(X, y, discrete_features):
    mi_scores = mutual_info_regression(X, y, discrete_features=discrete_features)
    mi_scores = pd.Series(mi_scores, name="MI Scores", index=X.columns)
    mi_scores = mi_scores.sort_values(ascending=False)
    return mi_scores

我们选择了涵盖一系列属性的四个特征。这些功能中的每一个在目标 Price 方面也都有很高的 MI 分数。我们将对数据进行标准化，因为这些特征自然不在同一尺度上。

features = ["highway_mpg", "engine_size", "horsepower", "curb_weight"]

X = df.copy()
y = X.pop('price')
X = X.loc[:, features]

# Standardize
X_scaled = (X - X.mean(axis=0)) / X.std(axis=0)

现在我们可以拟合 scikit-learn 的 PCA 估计器并创建主组件

from sklearn.decomposition import PCA

# Create principal components
pca = PCA()
X_pca = pca.fit_transform(X_scaled)

# Convert to dataframe
component_names = [f"PC{i+1}" for i in range(X_pca.shape[1])]
X_pca = pd.DataFrame(X_pca, columns=component_names)

X_pca.head()

拟合后，PCA 实例在其 components_ 属性中包含载荷。

loadings = pd.DataFrame(
    pca.components_.T,  # 转置 PCA 变换矩阵
    columns=component_names,  # 列名是主成分
    index=X.columns,  # 行索引是原始特征名
)
loadings

回想一下，组件载荷的符号和大小告诉我们它被捕获了什么样的变化。第一个组件 （PC1） 显示了油耗较差的大型、强大的车辆与油耗良好的较小、更经济的车辆之间的对比。我们可以称之为 “豪华/经济” 轴。下图显示，我们选择的四个功能主要沿 Luxury/Economy 轴变化。

plot_variance(pca);

我们还看一下组件的 MI 分数。毫不奇怪，PC1 的信息量很大，尽管其余组件尽管差异很小，但仍然与价格有重要关系。检查这些组件可能是值得的，以发现 Luxury/Economy 主轴未捕获的关系。

mi_scores = make_mi_scores(X_pca, y, discrete_features=False)
mi_scores

Part6 -- Target Encoding

在本部分，Target Encoding（目标编码）是适用于离散特征，这是一种将类别编码为数字的方法，例如 one-hot 或 label 编码，不同之处在于它还使用 target 来创建编码。这就是我们所说的监督式特征工程技术。

Target Encoding -- 目标编码

目标编码 -- 将要素的类别替换为从目标派生的某个数字的任何类型的编码。

一个简单而有效的版本是应用Part3中的 组聚合，例如平均值。使用 Automobiles 数据集，这将计算每辆车品牌的平均价格：

autos["make_encoded"] = autos.groupby("make")["price"].transform("mean")

这种目标编码有时称为 mean 编码（mean encoding） 。应用于二进制目标，也称为 bin 计数（bin counting） 。（您可能会遇到的其他名称包括：似然编码（likelihood encoding）、影响编码（impact encoding）和留一编码（leave-one-out encoding）。

Smoothing -- 平滑

但是，像这样的编码会带来几个问题。首先是未知的类别 。目标编码会产生过度拟合的特殊风险，这意味着它们需要在独立的“编码”拆分上进行训练。当您将编码联接到将来的拆分时，Pandas 将填充编码拆分中不存在的任何类别的缺失值。这些缺失的值必须以某种方式进行估算。

其次是稀有类别 。当某个类别在数据集中只出现几次时，对其组计算的任何统计数据都不太可能非常准确。在 Automobiles 数据集中，mercurcy make 只出现一次。我们计算的“平均”价格只是那辆车的价格，这可能不是很能代表我们未来可能看到的任何 Mercuries。目标编码罕见类别可能会使过度拟合的可能性更大。

这些问题的解决方案是添加平滑。 这个想法是将品类内平均值与总体平均值混合。稀有类别在其类别平均值上的权重较低，而缺失的类别仅获得总体平均值。

encoding = weight * in_category + (1 - weight) * overall

其中 weight 是根据类别频率计算的介于 0 和 1 之间的值。

确定 weight 值的一种简单方法是计算 m 估计值：

weight = n / (n + m)

 其中 n 是该类别在数据中出现的总次数。参数 m 确定 “smoothing factor”。m 值越大，总体估计的权重就越大。

在 Automobiles 数据集中，有三辆品牌为 chevrolet 的汽车。如果您选择 m=2.0，则雪佛兰 类别将使用雪佛兰平均价格的 60% 加上总平均价格的 40% 进行编码。

chevrolet = 0.6 * 6000.00 + 0.4 * 13285.03

当 m 选择值时，请考虑您预期的类别的噪点程度。每个品牌的车辆价格差异是否很大？您需要大量数据才能获得良好的估计吗？如果是这样，最好为 m 选择更大的值;如果每个品牌的平均价格相对稳定，那么较小的值就可以了。

Target 编码的使用案例

Target 编码非常适合：

1.高基数特征 -- 具有大量类别的特征编码可能很麻烦：独热编码会生成太多特征，而替代方法（如标签编码）可能不适合该特征。目标编码使用特征最重要的属性（它与目标的关系）为类别派生数字。

2.域激励特征 ：根据以前的经验，您可能会怀疑分类特征应该很重要，即使它在特征量度方面的得分很低。目标编码有助于揭示特征的真实信息量。

---------------------------------------------------------------------------------------------------------------------------------

示例 -- MovieLens1M

 MovieLens1M 数据集包含 MovieLens 网站用户的 100 万部电影评分，其中包含描述每个用户和电影的特征。

Number of Unique Zipcodes: 3439

Zipcode 功能具有 3000 多个类别，非常适合目标编码，并且此数据集的大小（超过 100 万行）意味着我们可以腾出一些数据来创建编码。

首先，我们将创建一个 25% 的拆分来训练目标编码器。

X = df.copy()
y = X.pop('Rating')

X_encode = X.sample(frac=0.25)
y_encode = y[X_encode.index]
X_pretrain = X.drop(X_encode.index)
y_train = y[X_pretrain.index]

scikit-learn-contrib 中的 category_encoders 包实现了一个 m-estimate 编码器，我们将使用它来编码我们的 Zipcode 功能。

from category_encoders import MEstimateEncoder

# 创建编码器. 选择 m 来控制噪声.
encoder = MEstimateEncoder(cols=["Zipcode"], m=5.0)

# 训练编码器
encoder.fit(X_encode, y_encode)

# 进行目标编码转换
X_train = encoder.transform(X_pretrain)

让我们将编码的值与目标进行比较，看看我们的编码可能提供多少信息。

plt.figure(dpi=90)
ax = sns.distplot(y, kde=False, norm_hist=True)
ax = sns.kdeplot(X_train.Zipcode, color='r', ax=ax)
ax.set_xlabel("Rating")
ax.legend(labels=['Zipcode', 'Rating']);

编码的 Zipcode 特征的分布大致遵循实际评级的分布，这意味着电影观看者在各个邮政编码的评级差异很大，因此我们的目标编码能够捕获有用的信息。

完结撒花！大家有什么问题可以在评论区进行讨论