27.用红黑树封装实现mymap和myset

一、分析stl源码中map和set对应的头文件<map>,<set>

#ifndef __SGI_STL_MAP
#define __SGI_STL_MAP

#ifndef __SGI_STL_INTERNAL_TREE_H
#include <stl_tree.h>
#endif
#include <stl_map.h>
#include <stl_multimap.h>

#ifndef __SGI_STL_SET
#define __SGI_STL_SET

#ifndef __SGI_STL_INTERNAL_TREE_H
#include <stl_tree.h>
#endif
#include <stl_set.h>
#include <stl_multiset.h>

可以发现都包含了stl_tree这个头文件，而这个stl_tree中，本质是一个红黑树的模板。

分析：set和map通过组合的方式，将一颗红黑树封装成队友的map和set。第一个参数传的都是键值Key的类型，第二个参数传的是节点的数据的类型，对于set来说有些多余，毕竟都是Key，但对于map来说是必要的，否则不知道pair<const Key,value>，不知道value的类型。

二、使用红黑树封装map和set，实现插入和迭代器

因此对于红黑树的节点的设计如下：

//T为节点的数据类型
template<class T>
struct RBTreeNode
{
	// 这里更新控制平衡也要加入parent指针
	T _data;
	RBTreeNode<T>* _left;
	RBTreeNode<T>* _right;
	RBTreeNode<T>* _parent;
	Colour _col;
	RBTreeNode(const T& data)
		:_data(data)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _col(RED)
	{}
};

但是如果仅按照第一个参数传Key，第二个参数传节点的数据类型。由于无法区分到底是T到底是Key还是pair<const Key,value>，插入的时候拿到的只是T，指针也是指向T类型，无法区分，因此要在map和set处传一个仿函数来方便insert时获取对应的Key值，以便于比较。

仿函数实现在map和set的内部（存疑）

set的仿函数 

	private:
		struct KeyOfT
		{
			const K& operator()(const K& key) const
			{
				return key;
			}
		};

map的仿函数：

	private:
		struct KeyOfT
		{
			const K& operator()(const pair<const K, V>& kv) const
			{
				return kv.first;
			}
		};

RBTree_iterator设计：

为了同时支持iterator和const_iterator，可以通过以下方式：

typedef RBTree_iterator<T, T&, T*> iterator;
typedef RBTree_iterator<T, const T&, const T*> const_iterator;

iterator和const_iterator唯一区别就是operator*和operator->的返回值类型不同，可以通过传const T&和constT*的方式使得返回值类型不同，只需在RBTree_iterator处接受即可。
 

template<class T,class Ref,class Ptr>
class RBTree_iterator
{
	typedef RBTreeNode<T> Node;
	typedef RBTree_iterator<T, Ref, Ptr> Self;
public:
	RBTree_iterator(Node* cur, Node* root)
		:_cur(cur)
		, _root(root)
	{}
	Ref operator*()
	{
		return _cur->_data;
	}
	Ptr operator->()
	{
		return &(_cur->_data);
	}
    //...
};

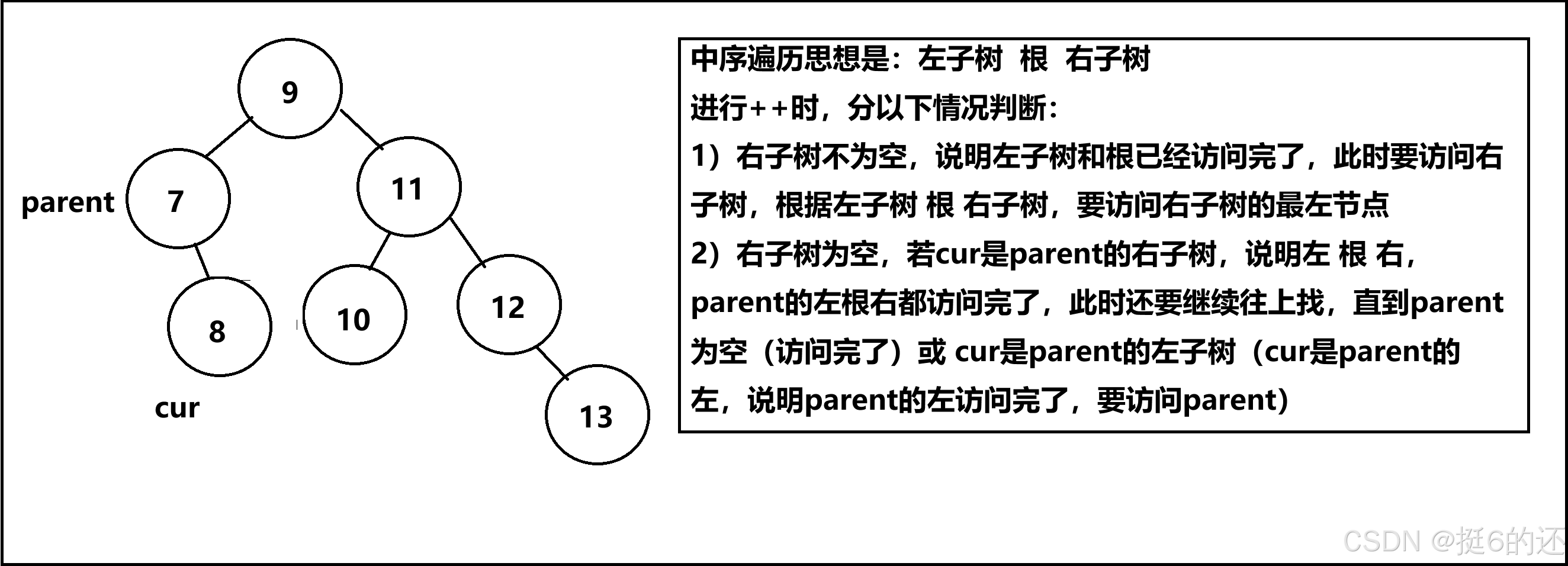
map和set是双向迭代器，设计时包含++和--，具体设计按以下分析

如上图所述。

需要注意的是：为什么能确定cur是parent左子树的根时parent的左访问完了？

原因：因为右不为空是优先访问右的最左节点的，正因为这个前提条件，可以确定当cur的右为空时，且cur为parent的右子树时，当前parent已经访问完了，需要向上找，直到作为parent左或parent为空。cur为parent左时，parent的左访问完了，要访问parent的根就是parent；parent为空时，在向上找之前，cur就是整颗树的最右节点，此时截止了。
代码实现：

Self& operator++()
{
	assert(_cur);
	Node* cur = _cur;
	//cur的右不为空，左 根 右，
	// 说明左和根已经访问完了
	//现在要访问右子树的最左节点(最小节点)
	if (cur->_right)
	{
		Node* minRight = cur->_right;
		while (minRight->_left)
		{
			minRight = minRight->_left;
		}
		_cur = minRight;
	}
	else
	{
		Node* parent = cur->_parent;
		//如果当前节点是父亲的右
		// 说明父亲的左子树 父亲的根 父亲的右子树 都访问完了
		//此时还要继续向上找，直到cur为父亲的左
		//cur为父亲的左代表父亲的左子树访问完了，访问父亲的根
		while (parent && parent->_right == cur)
		{
			cur = parent;
			parent = cur->_parent;
		}
		//不论是 空 或是 非空，都是_cur等于parent
		_cur = parent;
	}
	return *this;
}

operator--与++类似，只不过是右 根 左的顺序。

但若要实现--end()达到反向遍历的效果，可以特殊处理，只不过要传root根节点的指针，当_cur为nullptr即end()时，让_cur等于中序遍历的最后一个（即根的最右节点的指针）

//中序左 根 右
//与++逻辑类似，不过是右 根 左
Self& operator--()
{
	//若要实现能反向遍历，
	//--到中序的最后一个，即根的最右节点
	if (_cur == nullptr)
	{
		Node* cur = _root;
		while (cur && cur->_right)
		{
			cur = cur->_right;
		}
		_cur = cur;
		return *this;
	}
	Node* cur = _cur;
	// 右 根 左
	//cur的左不为空，
	// 说明右访问完了，根也访问完了，
	// 上一个需要访问的就是左子树的最右节点
	if (cur->_left)
	{
		Node* maxLeft = cur->_left;
		while (maxLeft->_right)
		{
			maxLeft = maxLeft->_right;
		}
		_cur = maxLeft;
	}
	else
	{
		//--也会走到空，与++走到空含义不同
		//--是右根左的空，++是左根右的空
		Node* parent = cur->_parent;
		//右 根 左
		//如果cur是parent的左，
		// 说明parent已经访问完了，要向上找
		//直到cur为parent的右
		while (parent && parent->_left == cur)
		{
			cur = parent;
			parent = cur->_parent;
		}
		//不论是 空 或是 非空，都是_cur等于parent
		_cur = parent;
	}
	return *this;
}

封装RBTree时注意事项：

stl源码中把map中的RBTree<K, pair<const K, V>, KeyOfT>类型重命名为repe_type，这种方式很好，因为在map和set中为了使用的方便，且为了让重命名iterator时不用写那么多。

重命名如下：

set

public:
	typedef typename RBTree<K,const K, KeyOfT> tree_type;
	typedef typename tree_type::iterator iterator;

map

public:
	typedef typename RBTree<K, pair<const K, V>, KeyOfT> tree_type;
	typedef typename tree_type::iterator iterator;

最后就是map的operator[]的实现：

operator[]，本质就是调用insert。若不存在，则插入，返回对应迭代器位置的value的引用。若存在，则不插入，返回对应迭代器位置的value的引用。

实现如下：

V& operator[](const K& key)
{
	pair<iterator, bool> ret = insert({ key,V() });
	iterator it = ret.first;
	return (*it).second;
}

 以下就是所以实现的源码：

RBTree.h

#pragma once
#include<assert.h>

// 枚举值表示颜色
enum Colour
{
	RED,
	BLACK
};

//T为节点的数据类型
template<class T>
struct RBTreeNode
{
	// 这里更新控制平衡也要加入parent指针
	T _data;
	RBTreeNode<T>* _left;
	RBTreeNode<T>* _right;
	RBTreeNode<T>* _parent;
	Colour _col;
	RBTreeNode(const T& data)
		:_data(data)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _col(RED)
	{}
};

template<class T,class Ref,class Ptr>
class RBTree_iterator
{
	typedef RBTreeNode<T> Node;
	typedef RBTree_iterator<T, Ref, Ptr> Self;
public:
	RBTree_iterator(Node* cur, Node* root)
		:_cur(cur)
		, _root(root)
	{}
	Ref operator*()
	{
		return _cur->_data;
	}
	Ptr operator->()
	{
		return &(_cur->_data);
	}

	bool operator==(const Self& it) const
	{
		return _cur == it._cur;
	}
	bool operator!=(const Self& it) const
	{
		return _cur != it._cur;
	}

	Self& operator++()
	{
		assert(_cur);
		Node* cur = _cur;
		//cur的右不为空，左 根 右，
		// 说明左和根已经访问完了
		//现在要访问右子树的最左节点(最小节点)
		if (cur->_right)
		{
			Node* minRight = cur->_right;
			while (minRight->_left)
			{
				minRight = minRight->_left;
			}
			_cur = minRight;
		}
		else
		{
			Node* parent = cur->_parent;
			//如果当前节点是父亲的右
			// 说明父亲的左子树 父亲的根 父亲的右子树 都访问完了
			//此时还要继续向上找，直到cur为父亲的左
			//cur为父亲的左代表父亲的左子树访问完了，访问父亲的根
			while (parent && parent->_right == cur)
			{
				cur = parent;
				parent = cur->_parent;
			}
			//不论是 空 或是 非空，都是_cur等于parent
			_cur = parent;
		}
		return *this;
	}

	//中序左 根 右
	//与++逻辑类似，不过是右 根 左
	Self& operator--()
	{
		//若要实现能反向遍历，
		//--到中序的最后一个，即根的最右节点
		if (_cur == nullptr)
		{
			Node* cur = _root;
			while (cur && cur->_right)
			{
				cur = cur->_right;
			}
			_cur = cur;
			return *this;
		}
		Node* cur = _cur;
		// 右 根 左
		//cur的左不为空，
		// 说明右访问完了，根也访问完了，
		// 上一个需要访问的就是左子树的最右节点
		if (cur->_left)
		{
			Node* maxLeft = cur->_left;
			while (maxLeft->_right)
			{
				maxLeft = maxLeft->_right;
			}
			_cur = maxLeft;
		}
		else
		{
			//--也会走到空，与++走到空含义不同
			//--是右根左的空，++是左根右的空
			Node* parent = cur->_parent;
			//右 根 左
			//如果cur是parent的左，
			// 说明parent已经访问完了，要向上找
			//直到cur为parent的右
			while (parent && parent->_left == cur)
			{
				cur = parent;
				parent = cur->_parent;
			}
			//不论是 空 或是 非空，都是_cur等于parent
			_cur = parent;
		}
		return *this;
	}
private:
	Node* _cur;
	Node* _root;
};


//第一个参数传key，第二个参数传节点的数据类型
//第三个参数传仿函数，以便插入时获取节点的Key进行比较
template<class Key, class T,class KeyOfT>
class RBTree
{
public:
	typedef RBTreeNode<T> Node;
	typedef RBTree_iterator<T, T&, T*> iterator;
	typedef RBTree_iterator<T, const T&, const T*> const_iterator;
public:
	iterator Begin()
	{
		Node* cur = _root;
		while (cur && cur->_left)
		{
			cur = cur->_left;
		}
		return iterator(cur, _root);
	}
	iterator End()
	{
		return iterator(nullptr, _root);
	}

	~RBTree()
	{
		destory(_root);
	}
	
	pair<iterator,bool> Insert(const T& data)
	{
		if (_root == nullptr)
		{
			_root = new Node(data);
			_root->_col = BLACK;
			return { iterator(_root,_root),true };
		}
		KeyOfT kot;
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			//比cur小，往左走
			if (kot(cur->_data)> kot(data))
			{
				parent = cur;
				cur = parent->_left;
			}
			//比cur大，往右走
			else if (kot(cur->_data) < kot(data))
			{
				parent = cur;
				cur = parent->_right;
			}
			else
			{
				return { iterator(cur,_root),false };
			}
		}
	    Node* newnode = new Node(data);
		cur = newnode;
		//比parent小，链接在左边,否则链接在右边
		if (kot(data) < kot(parent->_data))
		{
			parent->_left = cur;
		}
		else
		{
			parent->_right = cur;
		}
		cur->_parent = parent;

		//调整部分
		//parent不为空 且 parent的颜色为红色就还要继续调整
		while (parent && parent->_col==RED)
		{
			//grandparent一定非NULL，
			// 因为如果parent如果是根节点，parent就是黑色的
			//parent是黑色的进不来循环
			Node* grandparent = parent->_parent;
			if (parent == grandparent->_left)
			{
				//     g              g
				//   p   u    或    p   u
				// c                 c
				Node* uncle = grandparent->_right;
				//无论cur在左还是右都不影响
				//uncle存在且为红
				if (uncle && uncle->_col == RED)
				{
					parent->_col = uncle->_col = BLACK;
					grandparent->_col = RED;
					//还要向上处理
					cur = grandparent;
					parent = cur->_parent;
				}
				//uncle不存在 或者 uncle存在且为黑
				else
				{
					//     g
					//   p   u
					// c
					//cur为parent的左
					if (cur == parent->_left)
					{
						rotateR(grandparent);
						parent->_col = BLACK;
						grandparent->_col = RED;
						//旧的parent现在的grandparent
						// 已经为黑色了，不需要向上处理
						break;
					}
					//cur为parent的右，不是单纯一边高
					//双旋加变色
					else
					{
						//    g
						//  p   u
						//   c
						rotateL(parent);
						rotateR(grandparent);
						cur->_col = BLACK;
						grandparent->_col = RED;
						//旧的cur现在的grandparent
						//已经变为黑色了，不需要向上处理
						break;
					}
				}
			}
			else
			{
				//     g
				//   u   p
				//		   c
				Node* grandparent = parent->_parent;
				Node* uncle = grandparent->_left;
				//无论cur在左还是右，不影响
				if (uncle && uncle->_col == RED)
				{
					grandparent->_col = RED;
					uncle->_col = parent->_col = BLACK;
					//此时grandparent为红色，需要向上更新
					cur = grandparent;
					parent = cur->_parent;
				}
				// uncle存在且为黑 或者 uncle为空
				else
				{
					//     g
					//   u   p
					//		   c
					//单纯一边高，单旋加变色
					if (cur == parent->_right)
					{
						rotateL(grandparent);
						parent->_col = BLACK;
						grandparent->_col = RED;
						//旧parent新grandparent
						//此时已经为黑，停止更新
						break;
					}
					//    g
					//  u   p
					//    c
					//不是单纯一边高，双旋加变色
					else
					{
						rotateR(parent);
						rotateL(grandparent);
						cur->_col = BLACK;
						grandparent->_col = RED;
						//旧cur新grandparent
						//此时已经为黑，停止更新
						break;
					}
				}
			}
		}
		_root->_col = BLACK;
		return { iterator(newnode, _root), true };
	}
private:
	//右单旋
	void rotateR(Node* parent)
	{
		Node* grandparent = parent->_parent;
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		//1.判断parent是否是根，链接grandparent与subL
		if (grandparent == nullptr)
		{
			_root = subL;
		}
		else
		{
			if (grandparent->_left == parent)
			{
				grandparent->_left = subL;
			}
			else
			{
				grandparent->_right = subL;
			}
		}
		subL->_parent = grandparent;
		//2.链接subL和parent
		subL->_right = parent;
		parent->_parent = subL;
		//3.链接subLR和parent,subLR不为空,subLR的parent要链接parent
		parent->_left = subLR;
		if (subLR)
			subLR->_parent = parent;
	}

	//左单旋
	void rotateL(Node* parent)
	{
		Node* grandparent = parent->_parent;
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		//1.判断parent是否是根，链接grandparent与subR
		if (grandparent == nullptr)
		{
			_root = subR;
		}
		else
		{
			if (grandparent->_left == parent)
			{
				grandparent->_left = subR;
			}
			else
			{
				grandparent->_right = subR;
			}
		}
		subR->_parent = grandparent;
		//2.链接subR和parent
		subR->_left = parent;
		parent->_parent = subR;
		//3.链接subRL和parent
		parent->_right = subRL;
		if (subRL)
			subRL->_parent = parent;
	}

	void destory(Node* root)
	{
		if (root == nullptr)
			return;
		destory(root->_left);
		destory(root->_right);
		delete root;
		root = nullptr;
	}
private:
	Node* _root = nullptr;
};

Myset.h

#pragma once
#include"RBTree.h"

namespace quiteSix
{
	//template<class K>
	//struct KeyOfT
	//{
	//	const K& operator()(const K& key) const
	//	{
	//		return key;
	//	}
	//};

	template<class K>
	class set
	{
	private:
		struct KeyOfT
		{
			const K& operator()(const K& key) const
			{
				return key;
			}
		};
	public:
	typedef typename RBTree<K,const K, KeyOfT> tree_type;
	typedef typename tree_type::iterator iterator;
	public:
		pair<iterator, bool> insert(const K& data)
		{
			return _t.Insert(data);
		}
		iterator begin()
		{
			return _t.Begin();
		}
		iterator end()
		{
			return _t.End();
		}
	private:
		tree_type _t;
	};
}

Mymap.h

#pragma once
#include"RBTree.h"

namespace quiteSix
{
	//template<class K, class V>
	//struct KeyOfT
	//{
	//	const K& operator()(const pair<const K, V>& kv) const
	//	{
	//		return kv.first;
	//	}
	//};

	template<class K, class V>
	class map
	{
	private:
		struct KeyOfT
		{
			const K& operator()(const pair<const K, V>& kv) const
			{
				return kv.first;
			}
		};
	public:
		typedef typename RBTree<K, pair<const K, V>, KeyOfT> tree_type;
		typedef typename tree_type::iterator iterator;
	public:
		pair<iterator,bool> insert(const pair<const K, V>& _data)
		{
			return _t.Insert(_data);
		}
		iterator begin()
		{
			return _t.Begin();
		}
		iterator end()
		{
			return _t.End();
		}

		V& operator[](const K& key)
		{
			pair<iterator, bool> ret = insert({ key,V() });
			iterator it = ret.first;
			return (*it).second;
		}
	private:
		tree_type _t;
	};
}